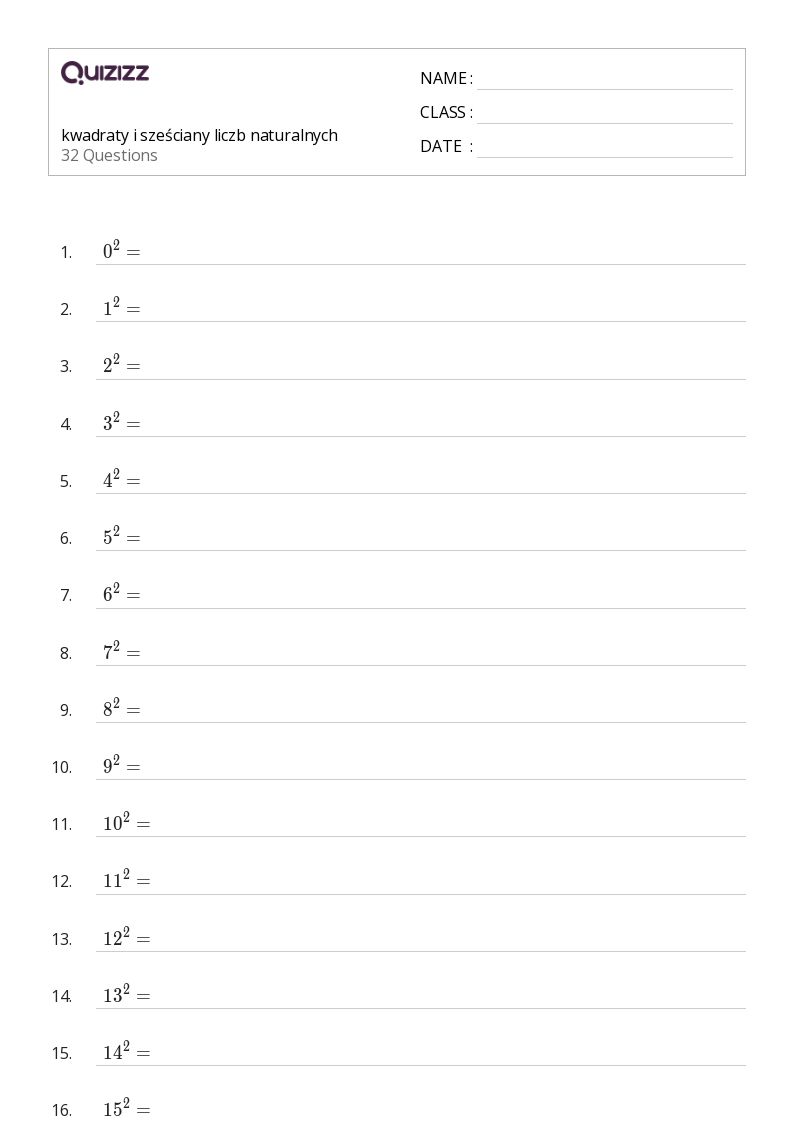
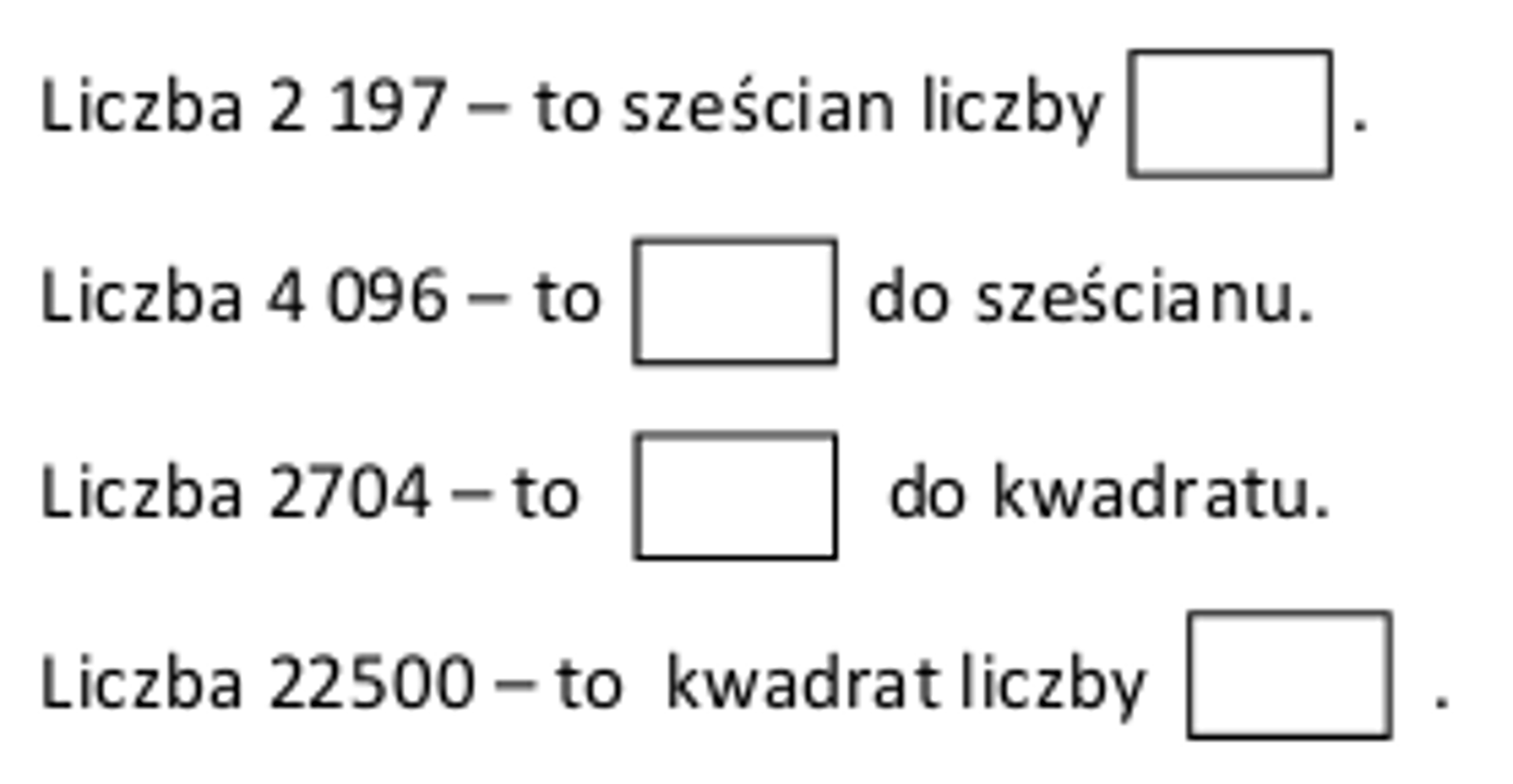
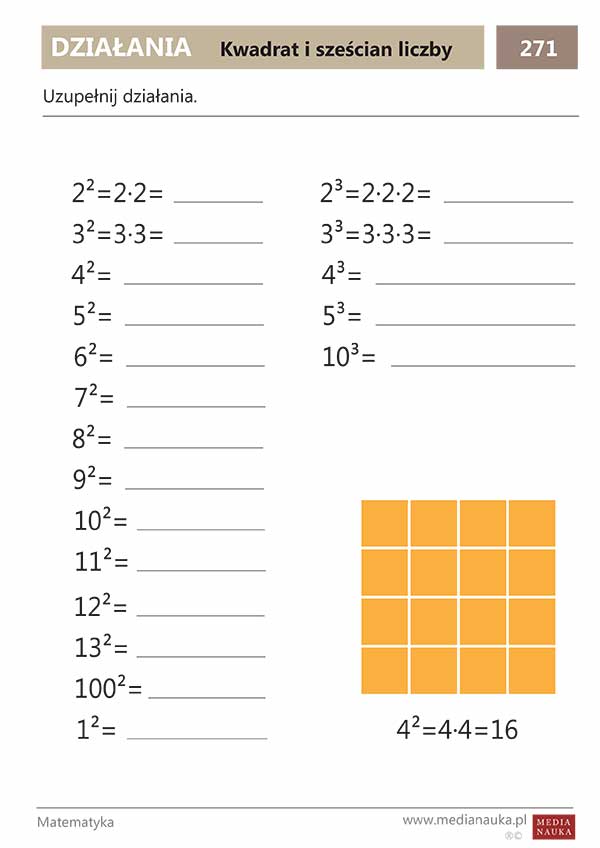Kwadraty I Sześciany Liczb Klasa 4 Zadania Do Druku

Witajcie, Drodzy Nauczyciele Klas Czwartych!

Przygotowanie uczniów do matematycznych wyzwań wymaga solidnych podstaw. Jednym z tematów, który może sprawić radość, a jednocześnie stanowić fundament dla dalszej nauki, jest wprowadzenie pojęcia kwadratów i sześcianów liczb. W tym artykule przyjrzymy się, jak skutecznie wprowadzić ten temat w klasie czwartej, uniknąć typowych błędów i sprawić, by nauka była angażująca.

Czym są kwadraty i sześciany liczb? Wyjaśnienie krok po kroku.

Zanim przystąpimy do zadań i kart pracy, kluczowe jest solidne zrozumienie, czym właściwie są kwadraty i sześciany liczb. Zacznijmy od kwadratów.

Kwadrat liczby to nic innego jak pomnożenie tej liczby przez samą siebie. Możemy to przedstawić w prosty sposób:

• 2 do kwadratu (zapisywane jako 2²) to 2 * 2 = 4
• 3 do kwadratu (zapisywane jako 3²) to 3 * 3 = 9
• 5 do kwadratu (zapisywane jako 5²) to 5 * 5 = 25

Wykorzystajmy wizualizacje! Narysuj na tablicy kwadrat o boku 2 cm. Podkreśl, że pole tego kwadratu (2cm * 2cm) wynosi 4 cm². Analogicznie, narysuj kwadrat o boku 3 cm, pokazując, że jego pole to 9 cm². To pomaga uczniom zrozumieć, skąd pochodzi nazwa "kwadrat".

Następnie przejdźmy do sześcianów. Sześcian liczby to pomnożenie tej liczby przez samą siebie… trzy razy! Czyli:

• 2 do sześcianu (zapisywane jako 2³) to 2 * 2 * 2 = 8
• 3 do sześcianu (zapisywane jako 3³) to 3 * 3 * 3 = 27
• 4 do sześcianu (zapisywane jako 4³) to 4 * 4 * 4 = 64

Tutaj wizualizacja jest nieco trudniejsza, ale nadal możliwa. Możesz pokazać uczniom kostkę Rubika (o ile taką posiadasz) i wyjaśnić, że jeśli każda krawędź kostki ma długość 3 cm, to objętość kostki (3cm * 3cm * 3cm) wynosi 27 cm³. Możesz też wykorzystać klocki do budowania sześcianów o różnych bokach.

Typowe błędy i jak ich unikać

Podczas wprowadzania pojęcia kwadratów i sześcianów, uczniowie często popełniają pewne typowe błędy. Ważne jest, aby być na nie przygotowanym i aktywnie im przeciwdziałać:

• Mylenie kwadratu z mnożeniem przez 2, a sześcianu z mnożeniem przez 3: To chyba najczęstszy błąd. Uczniowie widząc 3² myślą 3 * 2, a nie 3 * 3. Podobnie, 2³ bywa mylone z 2 * 3. Podkreślaj wielokrotnie, że potęga oznacza ile razy daną liczbę mnożymy przez samą siebie. Używaj kolorowych markerów, aby zaznaczać mnożone liczby w przykładach na tablicy.
• Brak zrozumienia notacji: Symbol „²” i „³” oznaczają potęgę i nie są jedynie ozdobnikami. Wyjaśnij, że zapis 5² to skrócony sposób na zapisanie 5 * 5. Regularnie pytaj uczniów, co oznaczają te symbole, aby utrwalić ich znaczenie.
• Trudności z obliczaniem większych liczb: Obliczanie np. 7² czy 6³ może sprawić trudność. Zachęcaj do rozkładania obliczeń na mniejsze kroki. Na przykład, zamiast od razu obliczać 7², można najpierw obliczyć 7 * 5, a potem dodać jeszcze 7 (7 * 7 = 7 * 5 + 7 * 2). Ćwiczcie te umiejętności regularnie.
• Problemy z zadaniami tekstowymi: Przekładanie problemu opisanego słowami na działanie matematyczne bywa wyzwaniem. Staraj się zadawać zadania tekstowe powiązane z realnymi sytuacjami, np. obliczanie pola kwadratowego placu zabaw lub objętości pudełka w kształcie sześcianu.

Jak uczynić naukę kwadratów i sześcianów angażującą?

Samo tłumaczenie i rozwiązywanie zadań może być dla uczniów nużące. Warto wprowadzić elementy, które uczynią naukę bardziej interaktywną i zabawną:

• Gry i zabawy:
  • "Kwadratowa Bingo": Przygotuj karty do bingo z liczbami będącymi kwadratami (np. 4, 9, 16, 25). Wywołuj liczby (np. "2 do kwadratu", "3 do kwadratu"), a uczniowie zaznaczają odpowiednie pola.
  • "Sześcianowa Kostka": Użyj kostki do gry. Uczeń rzuca kostką, a następnie podaje sześcian wylosowanej liczby. Można wprowadzić element rywalizacji, np. kto pierwszy poda prawidłowy wynik, zdobywa punkt.
  • "Kwadratowe i Sześcianowe Memory": Przygotuj pary kart, na jednej karcie zapisz działanie (np. 4²), a na drugiej jego wynik (16). Uczniowie grają w memory, szukając pasujących par.
• Wykorzystanie technologii:
  • Wykorzystaj interaktywne aplikacje i strony internetowe, które pozwalają na wizualizację kwadratów i sześcianów, np. poprzez rysowanie kwadratów i sześcianów o różnych bokach.
  • Wykorzystaj tablicę interaktywną do rozwiązywania zadań i prezentowania przykładów.
• Praca w grupach: Podziel klasę na mniejsze grupy i przydziel zadania, które wymagają współpracy. Na przykład, jedna grupa może obliczać kwadraty liczb od 1 do 10, a druga sześciany liczb od 1 do 5. Następnie grupy prezentują swoje wyniki.
• Zastosowania praktyczne: Pokaż uczniom, gdzie w życiu codziennym spotykamy się z kwadratami i sześcianami. Przykłady:
  • Obliczanie powierzchni pokoju (kwadrat)
  • Obliczanie objętości pudełka (sześcian)
  • Kafelki na ścianie (kwadraty)

Zadania do druku: Przykłady i dostosowanie

Przygotowując zadania do druku, pamiętaj o stopniowaniu trudności. Zacznij od prostych obliczeń, a następnie stopniowo wprowadzaj zadania tekstowe i bardziej złożone problemy. Przykładowe zadania:

• Oblicz:
  • 4² = ?
  • 6² = ?
  • 2³ = ?
  • 5³ = ?
• Uzupełnij:
  • …² = 9
  • …³ = 8
• Zadania tekstowe:
  • Plac zabaw ma kształt kwadratu o boku 7 metrów. Oblicz jego powierzchnię.
  • Pudełko ma kształt sześcianu o krawędzi 3 cm. Oblicz jego objętość.
• Porównaj:
  • Czy 3² jest większe od 2³?
  • Która liczba jest większa: 4² czy 3³?

Pamiętaj, aby zadania były dostosowane do poziomu uczniów. Jeśli widzisz, że sprawiają im trudność, wróć do podstaw i powtórz materiał. Nie bój się modyfikować zadań, aby były bardziej zrozumiałe i angażujące. Możesz również poprosić uczniów o wymyślanie własnych zadań, co dodatkowo wzmocni ich zrozumienie tematu.

Dostosowywanie zadań do różnych potrzeb uczniów

W klasie zawsze znajdują się uczniowie o różnych tempach uczenia się. Ważne jest, aby zadania były dostosowane do ich indywidualnych potrzeb.

• Dla uczniów potrzebujących dodatkowego wsparcia:
  • Zacznij od zadań z mniejszymi liczbami.
  • Używaj wizualizacji, np. rysunków i diagramów.
  • Podziel zadania na mniejsze kroki.
  • Pracuj indywidualnie lub w małych grupach.
• Dla uczniów, którzy szybko opanowali materiał:
  • Zadawaj bardziej złożone zadania, np. obliczanie kwadratów i sześcianów liczb dwucyfrowych.
  • Poproś o wymyślanie własnych zadań.
  • Wprowadź pojęcie pierwiastka kwadratowego i sześcianowego (jako wprowadzenie do kolejnych tematów).
  • Zaproponuj zadania wymagające logicznego myślenia i rozwiązywania problemów.

Podsumowanie i dalsze kroki

Wprowadzenie pojęcia kwadratów i sześcianów liczb w klasie czwartej to ważny krok w edukacji matematycznej. Kluczem do sukcesu jest solidne zrozumienie podstaw, unikanie typowych błędów oraz angażujące metody nauczania. Pamiętaj o wizualizacjach, grach i zabawach, a także o dostosowywaniu zadań do indywidualnych potrzeb uczniów. Regularne ćwiczenia i utrwalanie wiedzy sprawią, że uczniowie z łatwością opanują ten temat i będą gotowi na kolejne matematyczne wyzwania.

Powodzenia w pracy! Mam nadzieję, że ten artykuł będzie dla Ciebie pomocny. Pamiętaj, że najważniejsze to cierpliwość, kreatywność i pozytywne nastawienie!