Kulę O środku O Przecięto Płaszczyzną Przechodzącą Przez Punkt O1

Dobrze, spróbujmy to wyjaśnić w prosty sposób, tak jakbym tłumaczył to uczniowi na lekcji.

Wyobraź sobie kulę. To taka idealna piłka, prawda? Teraz wyobraź sobie, że masz nóż i przecinasz tę piłkę na pół. To przecięcie, ten ślad po nożu, to właśnie będzie dla nas ważny okrąg. Ale co, jeśli nie przecinasz jej dokładnie na pół, tylko trochę z boku?

Zatem, mamy kulę o środku w punkcie, który nazwiemy O. Teraz wyobraź sobie, że mamy płaszczyznę. Płaszczyzna to jak idealnie płaska kartka papieru, tylko nieskończenie duża. Ta płaszczyzna przechodzi przez jakiś inny punkt, który nazwiemy O1. O1 nie musi być środkiem naszej kuli (O). To kluczowe! Płaszczyzna ta przecina naszą kulę.

Co się stanie w miejscu, gdzie płaszczyzna przetnie kulę? Powstanie okrąg! Zawsze, gdy przetniesz kulę płaszczyzną, otrzymasz okrąg. Tylko w szczególnym przypadku, gdy płaszczyzna przechodzi dokładnie przez środek kuli (O), ten okrąg będzie największy możliwy – będzie to tzw. okrąg wielki kuli. Ale w naszym przypadku płaszczyzna przechodzi przez O1, który niekoniecznie jest O, więc okrąg, który powstanie, będzie mniejszy (lub równy w skrajnym przypadku, gdy O1 pokrywa się z O).

Spróbuj to sobie wyobrazić. Masz piłkę i kartkę papieru. Przebij kartkę szpilką (to punkt O1) i spróbuj tak ułożyć kartkę, żeby przecinała piłkę. Zobaczysz, że niezależnie od tego, jak ułożysz kartkę (oczywiście trzymając szpilkę w O1), na piłce powstanie okrąg. Ten okrąg leży na płaszczyźnie kartki i na powierzchni kuli jednocześnie.

Rozmiar tego okręgu będzie zależał od tego, jak blisko punktu O (środka kuli) przechodzi nasza płaszczyzna. Im bliżej środka, tym większy okrąg. A dokładniej, im mniejsza odległość pomiędzy punktem O (środek kuli) a płaszczyzną, tym większy promień okręgu powstałego z przecięcia. Jeśli ta odległość jest zerowa (czyli płaszczyzna przechodzi przez O), okrąg jest okręgiem wielkim kuli i ma największy możliwy promień – równy promieniowi kuli.

Jak znaleźć promień tego okręgu?

Skoro już wiemy, że powstaje okrąg, to naturalne pytanie brzmi: jak duży jest ten okrąg? Jak obliczyć jego promień?

Do tego potrzebujemy kilku informacji:

• R – promień kuli. To jest odległość od środka kuli (O) do dowolnego punktu na jej powierzchni.
• d – odległość od środka kuli (O) do naszej płaszczyzny. To jest najkrótsza odległość pomiędzy punktem O a płaszczyzną przechodzącą przez O1.

Załóżmy, że mamy te wartości. Wtedy, promień naszego okręgu, nazwijmy go r, możemy obliczyć z twierdzenia Pitagorasa! Tak, to naprawdę takie proste.

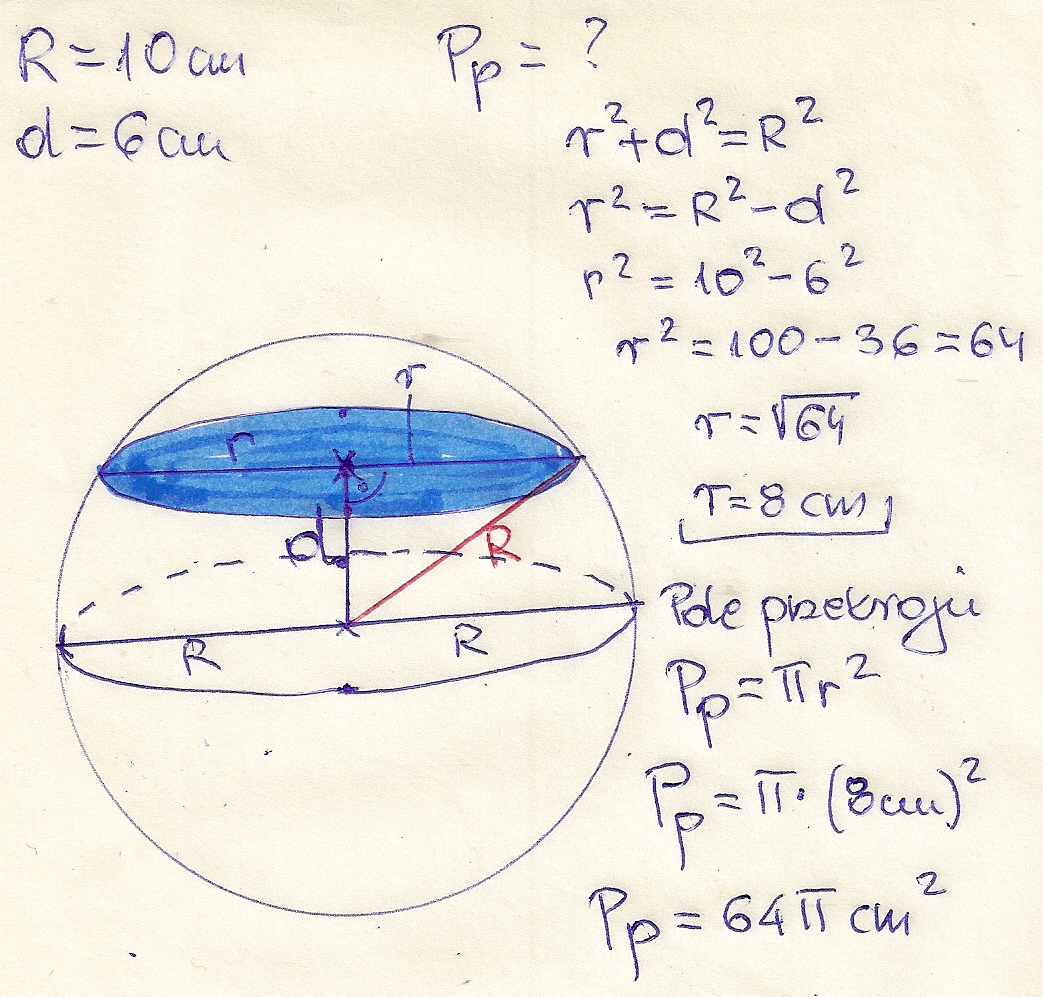
Wyobraź sobie trójkąt prostokątny. Jedna przyprostokątna to odległość d (od środka kuli do płaszczyzny). Druga przyprostokątna to promień naszego okręgu r (którego szukamy). A przeciwprostokątna to promień kuli R.

Zatem, mamy wzór:

r² + d² = R²

Żeby znaleźć r, musimy przekształcić ten wzór:

r² = R² - d²

A na koniec, wyciągamy pierwiastek kwadratowy, żeby dostać sam promień r:

r = √(R² - d²)

I to wszystko! Znając promień kuli (R) i odległość od środka kuli do płaszczyzny (d), możemy obliczyć promień okręgu powstałego z przecięcia.

Przykład:

Powiedzmy, że mamy kulę o promieniu R = 5 cm. Płaszczyzna przecina kulę w taki sposób, że odległość od środka kuli do tej płaszczyzny wynosi d = 3 cm. Jaki jest promień okręgu, który powstał z przecięcia?

Podstawiamy do wzoru:

r = √(R² - d²) r = √(5² - 3²) r = √(25 - 9) r = √16 r = 4 cm

Czyli promień okręgu wynosi 4 cm.

Co jeśli znamy tylko punkt O1?

Tutaj robi się trochę trudniej. Jeśli znamy tylko współrzędne punktu O1 i równanie płaszczyzny, musimy najpierw obliczyć odległość d od środka kuli (O) do płaszczyzny. Do tego potrzebujemy trochę więcej matematyki, ale zasada pozostaje ta sama.

Załóżmy, że mamy równanie płaszczyzny w postaci ogólnej:

Ax + By + Cz + D = 0

I znamy współrzędne środka kuli O: (x₀, y₀, z₀).

Wtedy odległość d możemy obliczyć ze wzoru:

d = |Ax₀ + By₀ + Cz₀ + D| / √(A² + B² + C²)

Gdzie:

• |...| oznacza wartość bezwzględną.
• A, B, C, D to współczynniki z równania płaszczyzny.
• x₀, y₀, z₀ to współrzędne środka kuli O.

Po obliczeniu d, możemy wrócić do naszego poprzedniego wzoru r = √(R² - d²), żeby obliczyć promień okręgu.

Podsumowując:

Przecięcie kuli płaszczyzną daje okrąg. Promień tego okręgu zależy od promienia kuli i odległości od środka kuli do płaszczyzny. Im bliżej płaszczyzna przechodzi środka kuli, tym większy okrąg. Mamy wzór r = √(R² - d²), który pozwala nam obliczyć promień okręgu, znając promień kuli (R) i odległość od środka kuli do płaszczyzny (d). Jeśli znamy tylko równanie płaszczyzny i współrzędne punktu O1, przez który przechodzi płaszczyzna, musimy najpierw obliczyć odległość d od środka kuli do płaszczyzny, używając odpowiedniego wzoru.