Krawędź Podstawy Ostrosłupa Prawidłowego Czworokątnego Ma Długość 6

Dobrze, posłuchajcie uważnie, bo omówimy wszystko, co istotne w kontekście ostrosłupa prawidłowego czworokątnego, gdzie krawędź podstawy ma długość 6. To zagadnienie ma wiele aspektów, od podstawowych obliczeń po bardziej zaawansowane rozważania geometryczne.

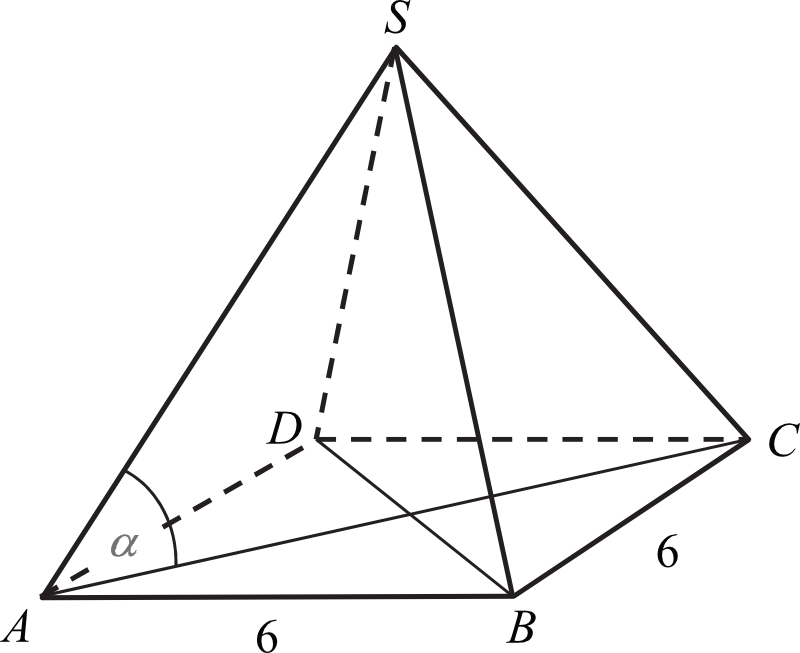
Zacznijmy od absolutnych fundamentów. Skoro mamy ostrosłup prawidłowy czworokątny, to wiemy, że jego podstawą jest kwadrat. To niezwykle ważna informacja, gdyż implikuje ona szereg konsekwencji geometrycznych. Każdy kąt w podstawie jest prosty (ma miarę 90 stopni), a wszystkie boki kwadratu są równe. Skoro krawędź podstawy ma długość 6, to każdy bok kwadratu podstawy ma dokładnie 6 jednostek długości.

To pozwala nam natychmiast obliczyć pole podstawy. Pole kwadratu to po prostu bok pomnożony przez bok, a więc 6 * 6 = 36. Zatem pole podstawy naszego ostrosłupa wynosi 36 jednostek kwadratowych. Wiedza o polu podstawy jest kluczowa do dalszych obliczeń, takich jak obliczenie objętości, jeśli znamy wysokość ostrosłupa.

Teraz przejdźmy do bardziej szczegółowych rozważań. Ostrosłup prawidłowy czworokątny posiada wierzchołek, który jest rzutowany prostopadle na środek podstawy. To kolejna fundamentalna cecha. Środek kwadratu to punkt przecięcia się jego przekątnych. A przekątne kwadratu o boku 6 przecinają się pod kątem prostym i dzielą się na połowy. Długość przekątnej kwadratu możemy obliczyć stosując twierdzenie Pitagorasa: a^2 + a^2 = d^2, gdzie a to długość boku, a d to długość przekątnej. W naszym przypadku: 6^2 + 6^2 = d^2, czyli 36 + 36 = d^2, stąd d^2 = 72, a d = sqrt(72) = 6 * sqrt(2).

Zatem, każda połowa przekątnej ma długość (6 * sqrt(2)) / 2 = 3 * sqrt(2). Ta wartość jest istotna, ponieważ tworzy ona trójkąt prostokątny wraz z wysokością ostrosłupa i krawędzią boczną. To kluczowe dla zrozumienia relacji przestrzennych wewnątrz ostrosłupa.

Wysokość i Krawędź Boczna

Jeśli znamy wysokość ostrosłupa (oznaczmy ją jako h), możemy obliczyć długość krawędzi bocznej (oznaczmy ją jako k). Zastosujemy do tego twierdzenie Pitagorasa w trójkącie prostokątnym utworzonym przez wysokość ostrosłupa, połowę przekątnej podstawy i krawędź boczną. Mamy zatem: h^2 + (3 * sqrt(2))^2 = k^2. Upraszczając: h^2 + 18 = k^2. Stąd k = sqrt(h^2 + 18).

Widzimy zatem, że długość krawędzi bocznej zależy bezpośrednio od wysokości ostrosłupa. Jeśli na przykład wysokość ostrosłupa wynosi 4, to krawędź boczna ma długość sqrt(4^2 + 18) = sqrt(16 + 18) = sqrt(34).

Analogicznie, jeśli znamy długość krawędzi bocznej, możemy obliczyć wysokość ostrosłupa: h = sqrt(k^2 - 18). Należy pamiętać, że krawędź boczna musi być dłuższa niż 3 * sqrt(2), w przeciwnym razie wysokość ostrosłupa byłaby liczbą zespoloną, co nie ma sensu w kontekście geometrii przestrzennej.

Objętość i Pole Powierzchni

Objętość ostrosłupa (V) obliczamy ze wzoru: V = (1/3) * Pole podstawy * Wysokość. W naszym przypadku: V = (1/3) * 36 * h = 12 * h. Objętość zależy zatem liniowo od wysokości ostrosłupa.

Pole powierzchni całkowitej ostrosłupa (Pc) to suma pola podstawy i pola powierzchni bocznej. Pole podstawy już znamy: 36. Powierzchnia boczna składa się z czterech identycznych trójkątów równoramiennych. Podstawą każdego z tych trójkątów jest krawędź podstawy (6), a ramionami są krawędzie boczne (k).

Aby obliczyć pole jednego trójkąta, potrzebujemy jego wysokości (wysokość ściany bocznej, oznaczmy ją jako ws). Możemy ją obliczyć, korzystając z twierdzenia Pitagorasa w trójkącie prostokątnym utworzonym przez połowę krawędzi podstawy (3), wysokość ściany bocznej (ws) i krawędź boczną (k): 3^2 + ws^2 = k^2, czyli 9 + ws^2 = k^2. Stąd ws = sqrt(k^2 - 9).

Pole jednego trójkąta (P_t) to (1/2) * Podstawa * Wysokość, czyli P_t = (1/2) * 6 * ws = 3 * sqrt(k^2 - 9). Ponieważ mamy cztery takie trójkąty, pole powierzchni bocznej (Pb) to 4 * P_t = 12 * sqrt(k^2 - 9).

Ostatecznie, pole powierzchni całkowitej (Pc) to Pole podstawy + Pole powierzchni bocznej, czyli Pc = 36 + 12 * sqrt(k^2 - 9). Pamiętajmy, że k = sqrt(h^2 + 18), więc możemy wyrazić pole powierzchni całkowitej wyłącznie w zależności od wysokości ostrosłupa: Pc = 36 + 12 * sqrt((h^2 + 18) - 9) = 36 + 12 * sqrt(h^2 + 9).

Widzimy więc, że zarówno objętość, jak i pole powierzchni całkowitej zależą od wysokości ostrosłupa. Znając wysokość, możemy jednoznacznie określić wszystkie istotne parametry geometryczne.

Dodatkową rzeczą, którą można rozważyć, jest kąt nachylenia ściany bocznej do płaszczyzny podstawy. Oznaczmy ten kąt jako alfa. Tangens tego kąta to stosunek wysokości ostrosłupa do połowy krawędzi podstawy, czyli tan(alfa) = h / 3. Stąd alfa = arctan(h/3). Zauważcie, że im większa wysokość ostrosłupa, tym większy kąt nachylenia ściany bocznej.

Podobnie, możemy rozważyć kąt nachylenia krawędzi bocznej do płaszczyzny podstawy. Oznaczmy ten kąt jako beta. Tangens tego kąta to stosunek wysokości ostrosłupa do połowy przekątnej podstawy, czyli tan(beta) = h / (3 * sqrt(2)). Stąd beta = arctan(h / (3 * sqrt(2))).

Wszystkie te zależności pozwalają nam na pełną analizę geometryczną ostrosłupa prawidłowego czworokątnego, którego krawędź podstawy ma długość 6. Rozważyliśmy pola, objętości, długości krawędzi, kąty nachylenia – wszystko, co istotne w tym kontekście. Pamiętajcie o podstawowych wzorach i twierdzeniach, a rozwiązywanie zadań z geometrii przestrzennej stanie się znacznie prostsze.