Krawędź Podstawy Graniastosłupa Prawidłowego Ma Długość 2

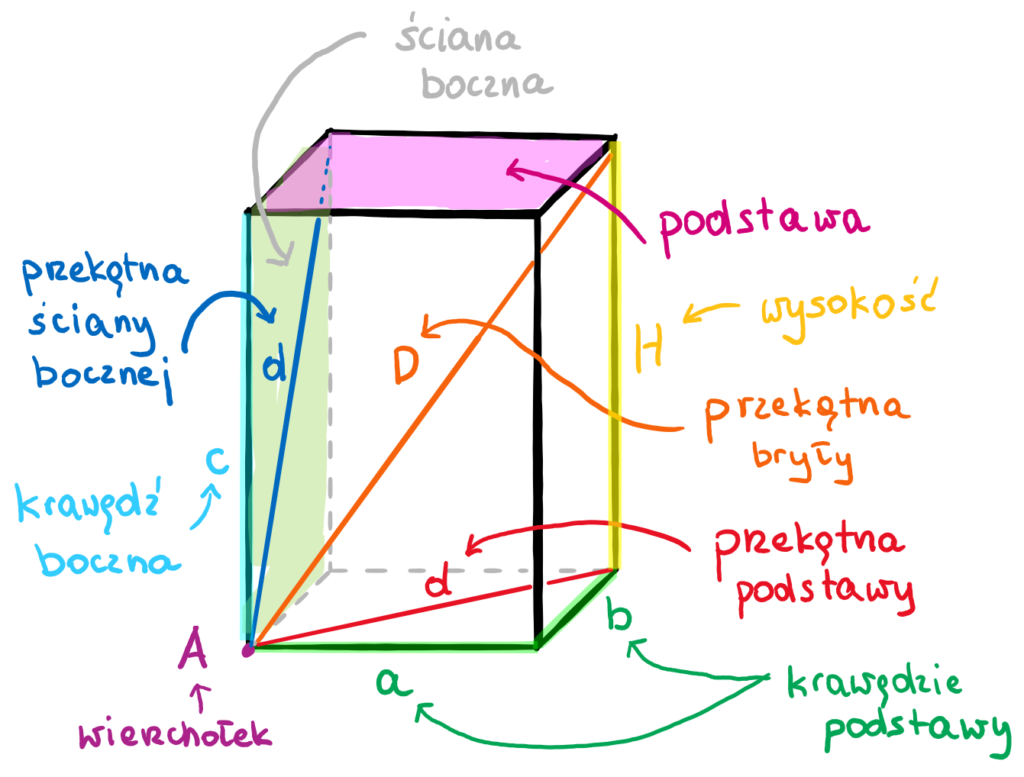
Zajmijmy się graniastosłupem prawidłowym, którego krawędź podstawy ma długość 2. To otwiera przed nami drzwi do fascynującego świata geometrii przestrzennej, gdzie możemy badać różnorodne właściwości i obliczenia.

Graniastosłup prawidłowy, ze względu na regularność swojej podstawy i prostopadłość ścian bocznych do podstawy, posiada wiele cech ułatwiających analizę. Krawędź podstawy o długości 2, to nasz punkt wyjścia do obliczeń pola powierzchni, objętości i innych parametrów.

Rozważmy najpierw graniastosłup prawidłowy trójkątny. Jego podstawą jest trójkąt równoboczny o boku długości 2. Aby obliczyć pole podstawy, skorzystamy ze wzoru na pole trójkąta równobocznego: (a^2 * sqrt(3))/4. Podstawiając a = 2, otrzymujemy (2^2 * sqrt(3))/4 = (4 * sqrt(3))/4 = sqrt(3). Pole podstawy wynosi zatem sqrt(3). Teraz, aby obliczyć objętość takiego graniastosłupa, potrzebujemy znać jego wysokość (H). Załóżmy, że wysokość graniastosłupa trójkątnego wynosi 5. Wtedy objętość graniastosłupa (V) obliczamy mnożąc pole podstawy przez wysokość: V = sqrt(3) * 5 = 5 * sqrt(3).

Ściany boczne takiego graniastosłupa to prostokąty. Każdy z nich ma wymiary 2 (długość krawędzi podstawy) na 5 (wysokość graniastosłupa). Pole jednej ściany bocznej wynosi więc 2 * 5 = 10. Ponieważ mamy trzy ściany boczne, pole powierzchni bocznej wynosi 3 * 10 = 30. Pole powierzchni całkowitej graniastosłupa trójkątnego to suma pola powierzchni bocznej i podwojonego pola podstawy: 30 + 2 * sqrt(3).

Przejdźmy teraz do graniastosłupa prawidłowego czworokątnego. Tutaj sytuacja jest nieco prostsza, ponieważ podstawą jest kwadrat o boku długości 2. Pole podstawy wynosi zatem 2 * 2 = 4. Załóżmy, że wysokość tego graniastosłupa wynosi 7. Wtedy objętość graniastosłupa wynosi 4 * 7 = 28.

Ściany boczne graniastosłupa czworokątnego to również prostokąty. Każdy z nich ma wymiary 2 na 7. Pole jednej ściany bocznej wynosi 2 * 7 = 14. Mamy cztery ściany boczne, więc pole powierzchni bocznej wynosi 4 * 14 = 56. Pole powierzchni całkowitej graniastosłupa czworokątnego to suma pola powierzchni bocznej i podwojonego pola podstawy: 56 + 2 * 4 = 56 + 8 = 64.

Możemy także rozważyć graniastosłup prawidłowy sześciokątny. Jego podstawą jest sześciokąt foremny o boku długości 2. Pole sześciokąta foremnego możemy obliczyć dzieląc go na sześć trójkątów równobocznych o boku 2. Pole jednego takiego trójkąta to sqrt(3), jak obliczyliśmy wcześniej. Zatem pole sześciokąta foremnego wynosi 6 * sqrt(3). Załóżmy, że wysokość graniastosłupa sześciokątnego wynosi 3. Wtedy objętość graniastosłupa wynosi 6 * sqrt(3) * 3 = 18 * sqrt(3).

Ściany boczne graniastosłupa sześciokątnego to prostokąty o wymiarach 2 na 3. Pole jednej ściany bocznej wynosi 2 * 3 = 6. Ponieważ mamy sześć ścian bocznych, pole powierzchni bocznej wynosi 6 * 6 = 36. Pole powierzchni całkowitej graniastosłupa sześciokątnego to suma pola powierzchni bocznej i podwojonego pola podstawy: 36 + 2 * (6 * sqrt(3)) = 36 + 12 * sqrt(3).

Dalsze Rozważania o Graniastosłupach Prawidłowych

Analizując różne typy graniastosłupów prawidłowych, warto zauważyć, że wzrost liczby boków w podstawie wpływa na stosunek pola powierzchni bocznej do pola podstawy. Im więcej boków ma podstawa, tym bardziej graniastosłup zbliża się kształtem do walca.

Możemy również badać przekątne graniastosłupów. W graniastosłupie prostym przekątna ściany bocznej tworzy trójkąt prostokątny z krawędzią podstawy i wysokością graniastosłupa. Na przykład, w graniastosłupie czworokątnym o krawędzi podstawy 2 i wysokości 7, przekątna ściany bocznej ma długość sqrt(2^2 + 7^2) = sqrt(4 + 49) = sqrt(53).

Ponadto, możemy rozważać kąty nachylenia przekątnych do płaszczyzny podstawy. W graniastosłupie czworokątnym przekątna graniastosłupa łączy przeciwległe wierzchołki podstaw. Jej długość można obliczyć korzystając z twierdzenia Pitagorasa w przestrzeni. Najpierw obliczamy długość przekątnej podstawy: sqrt(2^2 + 2^2) = sqrt(8) = 2 * sqrt(2). Następnie, długość przekątnej graniastosłupa wynosi sqrt((2 * sqrt(2))^2 + 7^2) = sqrt(8 + 49) = sqrt(57).

Kąt nachylenia tej przekątnej do płaszczyzny podstawy możemy obliczyć korzystając z funkcji trygonometrycznych. Tangens kąta nachylenia równa się stosunkowi wysokości graniastosłupa do długości przekątnej podstawy: tan(α) = 7 / (2 * sqrt(2)). Zatem α = arctan(7 / (2 * sqrt(2))).

Innym ciekawym zagadnieniem jest obliczanie pola powierzchni bocznej, gdy znamy objętość graniastosłupa i długość krawędzi podstawy. Załóżmy, że objętość graniastosłupa trójkątnego wynosi 10 * sqrt(3), a krawędź podstawy ma długość 2. Wtedy, jak obliczyliśmy wcześniej, pole podstawy wynosi sqrt(3). Zatem wysokość graniastosłupa wynosi V / Pole podstawy = (10 * sqrt(3)) / sqrt(3) = 10. Mając wysokość i długość krawędzi podstawy, możemy obliczyć pole powierzchni bocznej, które wynosi 3 * (2 * 10) = 60.

Warto pamiętać, że graniastosłupy prawidłowe stanowią podstawę do zrozumienia bardziej złożonych figur geometrycznych. Analiza ich właściwości pozwala na rozwinięcie umiejętności przestrzennego myślenia i rozwiązywania problemów geometrycznych.

Graniastosłupy to nie tylko abstrakcyjne figury, ale również obiekty, które możemy spotkać w życiu codziennym. Budynki, pudełka, a nawet niektóre elementy konstrukcyjne mają kształt graniastosłupów. Zrozumienie ich geometrii pozwala lepiej rozumieć otaczający nas świat.

Kształt graniastosłupów prawidłowych ma swoje zastosowanie także w architekturze. Wykorzystywane są do budowy kolumn, filarów, a także jako elementy dekoracyjne budynków. Regularność kształtu i proste kąty ułatwiają projektowanie i budowę konstrukcji.

Rozważania na temat graniastosłupów prawidłowych o krawędzi podstawy 2, pozwalają na utrwalenie wiedzy z zakresu geometrii przestrzennej, rozwijają umiejętność rozwiązywania problemów oraz pokazują zastosowanie matematyki w życiu codziennym.