Konstrukcje Geometryczne Sprawdzian Klasa 6 Gwo

Sprawdzian z konstrukcji geometrycznych w klasie 6 szkoły podstawowej to kluczowy moment w edukacji matematycznej. Wydawnictwo GWO (Gdańskie Wydawnictwo Oświatowe) oferuje materiały, które mają na celu przygotowanie uczniów do tego wyzwania. Niniejszy artykuł ma na celu przybliżenie zagadnień, które mogą pojawić się na takim sprawdzianie oraz wyjaśnienie najważniejszych aspektów związanych z konstrukcjami geometrycznymi.

Podstawowe Konstrukcje Geometryczne

Odcinek i Prosta

Na sprawdzianie z pewnością pojawią się zadania związane z rysowaniem i oznaczaniem odcinków oraz prostych. Ważne jest, aby uczeń potrafił odróżnić odcinek (który ma dwa końce), prostą (która nie ma końca) i półprostą (która ma jeden koniec). Użycie linijki i ołówka jest niezbędne do precyzyjnego wykonania tych konstrukcji. Należy pamiętać o dokładnym zaznaczaniu punktów końcowych odcinków. Błędne zaznaczenie może skutkować stratą punktów.

Kąty i Ich Rodzaje

Kolejnym istotnym elementem są kąty. Uczeń powinien znać rodzaje kątów: ostry, prosty, rozwarty i półpełny. Na sprawdzianie może pojawić się zadanie polegające na rozpoznawaniu i rysowaniu kątów o określonej mierze, np. za pomocą kątomierza. Konieczne jest precyzyjne użycie kątomierza i umiejętność odczytywania wartości kąta.

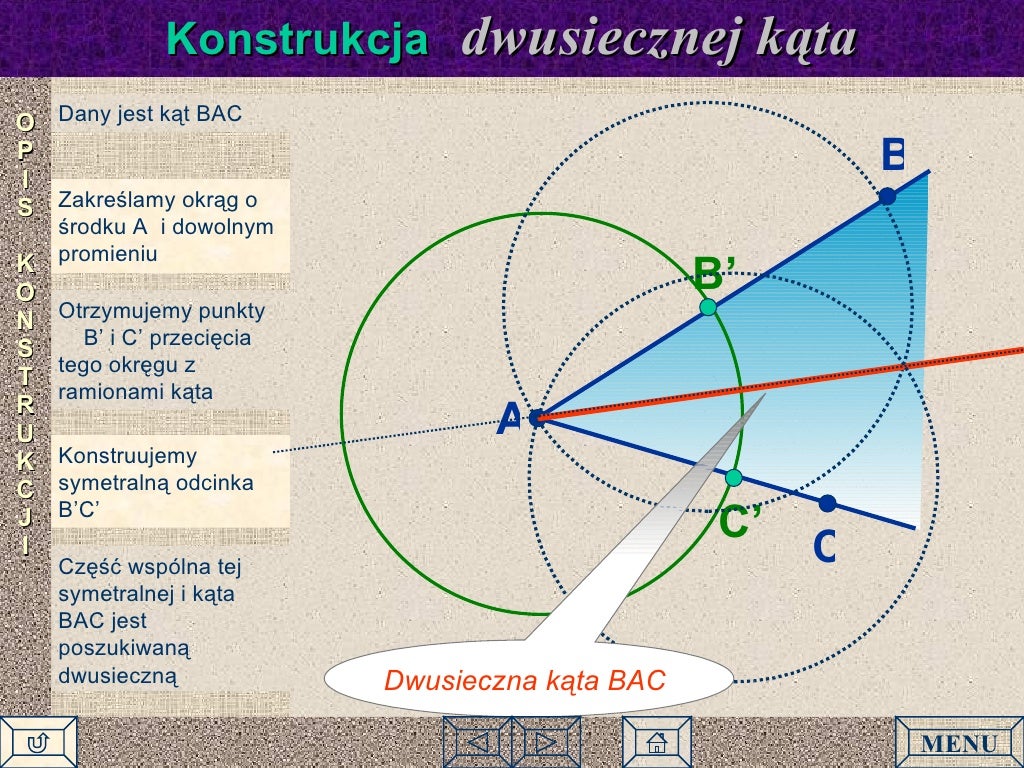
Konstrukcja Dwusiecznej Kąta

Dwusieczna kąta to prosta, która dzieli kąt na dwie równe części. Konstrukcja dwusiecznej kąta wymaga użycia cyrkla i linijki. Uczeń powinien znać kroki potrzebne do wykonania tej konstrukcji:

Z wierzchołka kąta kreślimy łuk cyrklem, który przecina ramiona kąta w dwóch punktach.
Z każdego z tych punktów kreślimy kolejne łuki cyrklem (o takim samym promieniu), które przecinają się wewnątrz kąta.
Łączymy wierzchołek kąta z punktem przecięcia łuków. Ta prosta jest dwusieczną kąta.

Konstrukcja Symetralnej Odcinka

Symetralna odcinka to prosta prostopadła do odcinka, przechodząca przez jego środek. Podobnie jak w przypadku dwusiecznej kąta, konstrukcja symetralnej wymaga użycia cyrkla i linijki. Kroki są następujące:

Z każdego końca odcinka kreślimy łuki cyrklem (o promieniu większym niż połowa długości odcinka), które przecinają się po obu stronach odcinka.
Łączymy punkty przecięcia łuków. Ta prosta jest symetralną odcinka.

Figury Geometryczne na Płaszczyźnie

Trójkąty i Ich Rodzaje

Uczniowie powinni znać rodzaje trójkątów ze względu na boki (równoboczny, równoramienny, różnoboczny) i kąty (ostrokątny, prostokątny, rozwartokątny). Na sprawdzianie może pojawić się zadanie polegające na skonstruowaniu trójkąta o podanych bokach lub kątach. Trzeba pamiętać o warunku trójkąta: suma długości dwóch dowolnych boków trójkąta musi być większa od długości trzeciego boku.

Konstrukcja Trójkąta o danych Bokach

Aby skonstruować trójkąt o danych bokach, należy użyć cyrkla i linijki. Najpierw rysujemy jeden z boków, a następnie z każdego końca tego boku kreślimy łuki o długościach odpowiadających pozostałym bokom. Punkt przecięcia łuków wyznacza trzeci wierzchołek trójkąta.

Czworokąty

Uczeń powinien znać podstawowe czworokąty, takie jak kwadrat, prostokąt, równoległobok, romb i trapez. Na sprawdzianie mogą pojawić się zadania polegające na rozpoznawaniu czworokątów na podstawie ich własności lub na rysowaniu czworokątów o zadanych cechach. Na przykład, konstrukcja kwadratu wymaga narysowania dwóch prostopadłych prostych przecinających się w jednym punkcie, a następnie odmierzenia na nich odcinków równej długości.

Praktyczne Zastosowania Konstrukcji Geometrycznych

Konstrukcje geometryczne nie są tylko abstrakcyjnymi rysunkami. Mają praktyczne zastosowanie w wielu dziedzinach, takich jak architektura, inżynieria, kartografia i grafika komputerowa. Na przykład, architekci używają konstrukcji geometrycznych do projektowania budynków i planowania przestrzeni, a inżynierowie do tworzenia precyzyjnych planów i schematów.

Przykład: Podział działki na dwie równe części można wykonać za pomocą konstrukcji symetralnej. Projektowanie logo firmy często opiera się na konstrukcjach geometrycznych, aby stworzyć estetyczny i harmonijny wygląd.

Przygotowanie do Sprawdzianu

Aby dobrze przygotować się do sprawdzianu z konstrukcji geometrycznych, warto:

Powtórzyć wszystkie definicje i zasady związane z figurami geometrycznymi i konstrukcjami.
Przećwiczyć rysowanie konstrukcji krok po kroku.
Rozwiązać zadania z podręcznika i zbioru zadań.
Zwrócić uwagę na precyzję rysowania.
Używać ołówka o odpowiedniej twardości i ostrego tempera.
Sprawdzić, czy masz wszystkie potrzebne przybory (linijkę, cyrkiel, kątomierz, ołówek, gumkę).

Pamiętaj! Systematyczna praca i zrozumienie zagadnień to klucz do sukcesu na sprawdzianie z konstrukcji geometrycznych. Nie bój się pytać nauczyciela o pomoc w przypadku trudności. Powodzenia!