Kolejność Wykonywania Działań Kl 6

Czy kiedykolwiek rozwiązywałeś zadanie matematyczne i otrzymałeś inny wynik niż Twój kolega? A może podczas gotowania, nie trzymając się kolejności składników, Twoje ciasto wyszło zakalcem? Często problemem nie jest brak wiedzy, a nieprzestrzeganie kolejności wykonywania działań. To fundament matematyki, klucz do poprawnego rozwiązywania zadań, a zrozumienie go ułatwia życie codzienne, nie tylko szkolne!

Ten artykuł jest dla Ciebie, uczniu klasy 6, który chce raz na zawsze zrozumieć, jak unikać błędów w obliczeniach i czuć się pewnie na sprawdzianach. Razem przejdziemy przez zasady, przykłady i przydatne wskazówki, które pomogą Ci stać się mistrzem kolejności działań!

Dlaczego Kolejność Wykonywania Działań Jest Tak Ważna?

Wyobraź sobie, że masz do rozwiązania proste zadanie: 2 + 3 * 4. Co powinieneś zrobić najpierw? Jeśli dodasz 2 do 3, otrzymasz 5, a następnie pomnożysz przez 4, uzyskasz wynik 20. Jeśli natomiast najpierw pomnożysz 3 przez 4, otrzymasz 12, a następnie dodasz 2, otrzymasz wynik 14. Widzisz różnicę? Dwie różne odpowiedzi dla tego samego zadania!

Właśnie dlatego potrzebujemy jasnych zasad. Kolejność wykonywania działań to zbiór reguł, które mówią nam, w jakiej kolejności należy wykonywać operacje matematyczne, aby zawsze otrzymać prawidłowy wynik. Bez tego matematyka byłaby chaosem!

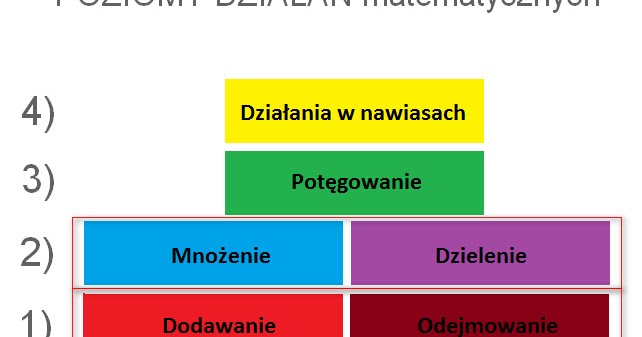
Zasady Kolejności Wykonywania Działań – Akronim PEMDAS/BODMAS

Najczęściej używanym akronimem, który pomaga zapamiętać kolejność działań, jest PEMDAS (w krajach anglojęzycznych) lub BODMAS (głównie w Wielkiej Brytanii). My skupimy się na uniwersalnych zasadach i dodamy kilka wskazówek.

1. Nawiasy (Parentheses/Brackets)

Wszystko, co jest w nawiasach, robimy jako pierwsze! Nawiasy to jak VIP w matematycznym świecie – mają pierwszeństwo. Mogą to być nawiasy okrągłe ( ), kwadratowe [ ] lub klamrowe { }. Rozwiązujemy je od wewnątrz na zewnątrz, zaczynając od nawiasów okrągłych, potem kwadratowych, a na końcu klamrowych.

Przykład: 5 * (2 + 3) = 5 * 5 = 25
Najpierw rozwiązujemy działanie w nawiasie (2+3), a dopiero potem mnożymy wynik przez 5.

2. Potęgowanie i Pierwiastkowanie (Exponents/Orders)

Potęgi i pierwiastki mają drugieństwo! Pamiętaj, że potęga to skrócony zapis mnożenia liczby przez samą siebie (np. 2³ = 2 * 2 * 2 = 8), a pierwiastek to działanie odwrotne do potęgowania (np. √9 = 3, bo 3 * 3 = 9).

Przykład: 2 + 3² = 2 + 9 = 11
Najpierw obliczamy potęgę (3² = 9), a dopiero potem dodajemy 2.

3. Mnożenie i Dzielenie (Multiplication and Division)

Mnożenie i dzielenie są równorzędne i wykonujemy je w kolejności, w jakiej występują od lewej do prawej! To ważna zasada – jeśli masz w zadaniu zarówno mnożenie, jak i dzielenie, nie rozwiązuj ich w jakiejś ulubionej kolejności, ale po kolei, czytając zadanie od lewej do prawej.

Przykład: 10 / 2 * 3 = 5 * 3 = 15
Najpierw dzielimy 10 przez 2, a dopiero potem mnożymy wynik przez 3. Gdybyśmy zrobili to odwrotnie (2*3=6, a potem 10/6), otrzymalibyśmy błędny wynik.

4. Dodawanie i Odejmowanie (Addition and Subtraction)

Dodawanie i odejmowanie są również równorzędne i wykonujemy je w kolejności, w jakiej występują od lewej do prawej! Podobnie jak w przypadku mnożenia i dzielenia, istotna jest kolejność od lewej do prawej.

Przykład: 8 - 3 + 2 = 5 + 2 = 7
Najpierw odejmujemy 3 od 8, a dopiero potem dodajemy 2.

Przykłady i Ćwiczenia

Spróbujmy rozwiązać kilka zadań, stosując poznane zasady:

Zadanie 1: 12 + 8 / 2 – 3 * 2

Rozwiązanie:
1. Dzielenie: 8 / 2 = 4
2. Mnożenie: 3 * 2 = 6
3. Dodawanie: 12 + 4 = 16
4. Odejmowanie: 16 - 6 = 10
Wynik: 10

Zadanie 2: (5 + 2) * 3 – 10 / 5

Rozwiązanie:
1. Nawias: (5 + 2) = 7
2. Mnożenie: 7 * 3 = 21
3. Dzielenie: 10 / 5 = 2
4. Odejmowanie: 21 - 2 = 19
Wynik: 19

Zadanie 3: 4² – (1 + 2 * 3)

Rozwiązanie:
1. Nawias (wewnętrzne mnożenie): 2 * 3 = 6
2. Nawias (dodawanie): 1 + 6 = 7
3. Potęgowanie: 4² = 16
4. Odejmowanie: 16 - 7 = 9
Wynik: 9

Spróbuj samodzielnie rozwiązać poniższe zadania:

20 - 5 * 2 + 8 / 4
(10 - 2) / 4 + 3²
15 + 3 * (6 - 4)

Wskazówki i Triki

Zapisuj kroki! Nie próbuj liczyć wszystkiego w pamięci. Zapisuj każdy krok działania, to pomoże Ci uniknąć błędów i łatwiej znajdziesz pomyłkę, jeśli się pojawi.
Podkreślaj działania. Podkreślaj działanie, które wykonujesz w danym kroku. To pomoże Ci utrzymać porządek.
Sprawdzaj wynik. Jeśli masz czas, sprawdź swój wynik, wykonując obliczenia od końca.
Praktyka czyni mistrza! Im więcej ćwiczysz, tym lepiej zapamiętasz kolejność wykonywania działań i tym szybciej będziesz rozwiązywać zadania.
Używaj kalkulatora z rozwagą. Kalkulator to świetne narzędzie, ale nie zastąpi on zrozumienia zasad. Używaj go do sprawdzania wyników, ale staraj się najpierw rozwiązywać zadania samodzielnie.

Kolejność Działań w Życiu Codziennym

Może Ci się wydawać, że kolejność wykonywania działań przydaje się tylko w szkole, ale tak naprawdę spotykasz się z nią na co dzień, choć często nie zdajesz sobie z tego sprawy. Na przykład:

Gotowanie: Jeśli przepis mówi "dodaj sól, a następnie wymieszaj", nie powinieneś najpierw wymieszać, a potem dodać soli. Kolejność jest ważna dla smaku i konsystencji potrawy.
Planowanie: Jeśli planujesz wycieczkę, musisz najpierw zarezerwować bilety, a potem hotel, inaczej możesz zostać bez noclegu.
Budżet: Jeśli chcesz obliczyć, ile pieniędzy zostanie Ci na koniec miesiąca, musisz najpierw obliczyć swoje dochody i wydatki, a potem je od siebie odjąć.

Podsumowanie

Kolejność wykonywania działań to fundament matematyki, który pomaga nam unikać błędów i rozwiązywać zadania w sposób logiczny i uporządkowany. Pamiętaj o akronimie PEMDAS/BODMAS i ćwicz regularnie, a szybko staniesz się mistrzem obliczeń! Nie bój się zadawać pytań nauczycielowi lub szukać dodatkowych materiałów w internecie. Zrozumienie kolejności działań to inwestycja w Twoją przyszłość, nie tylko szkolną!

Pamiętaj, matematyka jest jak układanka – każdy element musi być na swoim miejscu, aby całość miała sens. A kolejność wykonywania działań to instrukcja, która pomaga Ci ułożyć tę układankę poprawnie. Powodzenia!