Klasa 5 Własności Liczb Naturalnych

Hej! Zastanawiałeś/aś się kiedyś, jakie sekrety kryją liczby, których używamy na co dzień? W tym artykule, w prosty i przystępny sposób, odkryjemy własności liczb naturalnych – podstawę matematyki, którą poznajesz już w szkole podstawowej, a która jest kluczowa w bardziej zaawansowanych obliczeniach. Zaczynamy!

Czym są liczby naturalne?

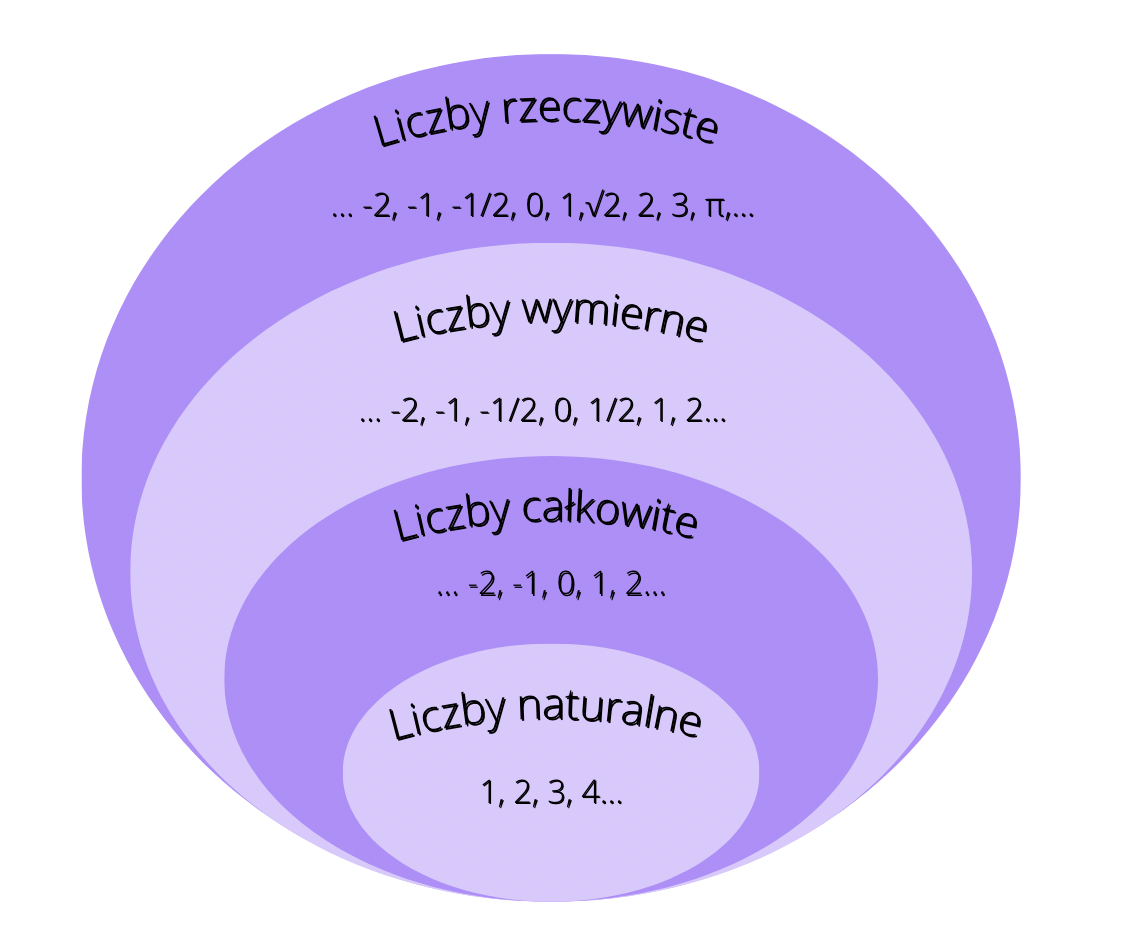
Zacznijmy od podstaw. Liczby naturalne to po prostu liczby, których używamy do liczenia. Wyobraź sobie, że liczysz jabłka w koszyku: jedno jabłko, dwa jabłka, trzy jabłka... To właśnie są liczby naturalne! Technicznie rzecz biorąc, są to liczby całkowite, nieujemne. Czyli:

1, 2, 3, 4, 5...

Czy zero jest liczbą naturalną? To zależy od definicji! W niektórych krajach (i w niektórych kontekstach matematycznych) zero jest włączane do zbioru liczb naturalnych, a w innych nie. Dla uproszczenia, w tym artykule będziemy traktować zero jako nie liczbę naturalną, chyba że zaznaczymy inaczej.

Ważne: Liczby naturalne to nie ułamki, liczby ujemne ani liczby zmiennoprzecinkowe (np. 3.14).

Działania na liczbach naturalnych

Na liczbach naturalnych możemy wykonywać podstawowe działania arytmetyczne: dodawanie, odejmowanie, mnożenie i dzielenie. Przyjrzyjmy się, które z tych działań zawsze dają w wyniku liczbę naturalną.

Dodawanie: Jeśli dodamy dwie liczby naturalne, zawsze otrzymamy liczbę naturalną. Na przykład: 2 + 3 = 5.
Mnożenie: Podobnie jak dodawanie, mnożenie dwóch liczb naturalnych zawsze daje liczbę naturalną. Na przykład: 4 * 6 = 24.
Odejmowanie: Tutaj robi się trochę trudniej. Jeśli odejmiemy od liczby naturalnej większą liczbę naturalną, otrzymamy liczbę ujemną, która nie jest liczbą naturalną. Na przykład: 3 - 5 = -2. Aby wynik odejmowania był liczbą naturalną, pierwsza liczba musi być większa lub równa drugiej. Na przykład: 7 - 2 = 5.
Dzielenie: Dzielenie liczb naturalnych rzadko daje w wyniku liczbę naturalną. Na przykład: 10 / 2 = 5 (liczba naturalna), ale 10 / 3 = 3.333... (nie jest liczbą naturalną).

Podzielność liczb naturalnych

Kluczową własnością liczb naturalnych jest ich podzielność. Mówimy, że liczba naturalna *a* jest podzielna przez liczbę naturalną *b*, jeśli wynik dzielenia *a* przez *b* jest liczbą naturalną (bez reszty). Inaczej mówiąc, *b* jest dzielnikiem *a*, a *a* jest wielokrotnością *b*.

Przykład:

Liczba 12 jest podzielna przez 2, 3, 4 i 6, ponieważ:

12 / 2 = 6
12 / 3 = 4
12 / 4 = 3
12 / 6 = 2

Wszystkie wyniki są liczbami naturalnymi. Zatem 2, 3, 4 i 6 są dzielnikami 12, a 12 jest wielokrotnością 2, 3, 4 i 6.

Cechy podzielności

Istnieją proste zasady, które pozwalają szybko sprawdzić, czy liczba jest podzielna przez inną liczbę, bez konieczności wykonywania dzielenia. Oto kilka najważniejszych:

Podzielność przez 2: Liczba jest podzielna przez 2, jeśli jej ostatnia cyfra jest parzysta (0, 2, 4, 6, 8). Na przykład: 124, 356, 1000 są podzielne przez 2.
Podzielność przez 3: Liczba jest podzielna przez 3, jeśli suma jej cyfr jest podzielna przez 3. Na przykład: 123 (1+2+3=6, a 6 jest podzielne przez 3), 456 (4+5+6=15, a 15 jest podzielne przez 3).
Podzielność przez 4: Liczba jest podzielna przez 4, jeśli liczba utworzona z jej dwóch ostatnich cyfr jest podzielna przez 4. Na przykład: 116 (16 jest podzielne przez 4), 2324 (24 jest podzielne przez 4).
Podzielność przez 5: Liczba jest podzielna przez 5, jeśli jej ostatnia cyfra to 0 lub 5. Na przykład: 25, 130, 1005.
Podzielność przez 9: Liczba jest podzielna przez 9, jeśli suma jej cyfr jest podzielna przez 9. Na przykład: 81 (8+1=9), 729 (7+2+9=18, a 18 jest podzielne przez 9).
Podzielność przez 10: Liczba jest podzielna przez 10, jeśli jej ostatnia cyfra to 0. Na przykład: 10, 120, 1000.

Znajomość tych cech podzielności bardzo ułatwia rozwiązywanie zadań matematycznych i pozwala szybko weryfikować wyniki.

Liczby pierwsze i liczby złożone

Wśród liczb naturalnych wyróżniamy dwie specjalne grupy: liczby pierwsze i liczby złożone.

Liczba pierwsza: To liczba naturalna większa od 1, która ma tylko dwa dzielniki: 1 i samą siebie. Przykładami liczb pierwszych są: 2, 3, 5, 7, 11, 13, 17, 19... Liczba 2 jest jedyną parzystą liczbą pierwszą.
Liczba złożona: To liczba naturalna większa od 1, która ma więcej niż dwa dzielniki. Przykładami liczb złożonych są: 4, 6, 8, 9, 10, 12, 14, 15... Każdą liczbę złożoną można przedstawić jako iloczyn liczb pierwszych (rozkład na czynniki pierwsze).

Liczba 1 nie jest ani liczbą pierwszą, ani liczbą złożoną. Traktowana jest jako jednostka.

Rozkład na czynniki pierwsze

Każdą liczbę złożoną można rozłożyć na iloczyn liczb pierwszych. Jest to bardzo przydatne w wielu zadaniach matematycznych, na przykład przy obliczaniu największego wspólnego dzielnika (NWD) i najmniejszej wspólnej wielokrotności (NWW).

Przykład: Rozkładamy liczbę 36 na czynniki pierwsze:

36 = 2 * 18 = 2 * 2 * 9 = 2 * 2 * 3 * 3 = 2² * 3²

Zatem czynniki pierwsze liczby 36 to 2 i 3.

Największy Wspólny Dzielnik (NWD) i Najmniejsza Wspólna Wielokrotność (NWW)

Dwa ważne pojęcia związane z podzielnością to największy wspólny dzielnik (NWD) i najmniejsza wspólna wielokrotność (NWW) dwóch lub więcej liczb.

NWD: Największy wspólny dzielnik dwóch (lub więcej) liczb naturalnych to największa liczba naturalna, która dzieli te liczby bez reszty.
NWW: Najmniejsza wspólna wielokrotność dwóch (lub więcej) liczb naturalnych to najmniejsza liczba naturalna, która jest wielokrotnością wszystkich tych liczb.

Przykład: Obliczmy NWD i NWW liczb 12 i 18.

Dzielniki liczby 12: 1, 2, 3, 4, 6, 12

Dzielniki liczby 18: 1, 2, 3, 6, 9, 18

Wspólne dzielniki: 1, 2, 3, 6

NWD(12, 18) = 6

Wielokrotności liczby 12: 12, 24, 36, 48, 60, 72...

Wielokrotności liczby 18: 18, 36, 54, 72, 90...

Wspólne wielokrotności: 36, 72...

NWW(12, 18) = 36

Sposób na obliczenie NWD i NWW z wykorzystaniem rozkładu na czynniki pierwsze:

1. Rozkładamy obie liczby na czynniki pierwsze:

12 = 2² * 3

18 = 2 * 3²

2. NWD: Bierzemy czynniki pierwsze występujące w obu rozkładach z najmniejszą potęgą:

NWD(12, 18) = 2¹ * 3¹ = 2 * 3 = 6

3. NWW: Bierzemy wszystkie czynniki pierwsze występujące w rozkładach z największą potęgą:

NWW(12, 18) = 2² * 3² = 4 * 9 = 36

Zastosowania w życiu codziennym

Własności liczb naturalnych mają zastosowanie w wielu sytuacjach w życiu codziennym. Na przykład:

Dzielenie się: Jeśli chcesz sprawiedliwie podzielić ciasto na kilka kawałków dla swoich przyjaciół, musisz użyć swojej wiedzy na temat podzielności.
Planowanie: Podczas planowania imprezy, obliczenie ile jedzenia potrzebujesz, wymaga użycia liczb naturalnych i podstawowych działań arytmetycznych.
Gotowanie: Receptury często wymagają pomiaru składników w określonych proporcjach, co wiąże się z wykorzystaniem liczb naturalnych i ich własności.
Finanse: Zarządzanie budżetem domowym, obliczanie wydatków i oszczędności, wszystko to opiera się na liczbach naturalnych i ich własnościach.

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć własności liczb naturalnych. To tylko wstęp do fascynującego świata matematyki. Pamiętaj, że regularne ćwiczenia i rozwiązywanie zadań to najlepszy sposób na utrwalenie wiedzy. Powodzenia!