Katy Przylegle I Wierzcholkowe Zadania

Kąty przyległe i kąty wierzchołkowe to fundamentalne pojęcia w geometrii euklidesowej. Rozumienie ich właściwości jest kluczowe dla rozwiązywania bardziej złożonych problemów geometrycznych, a także dla zrozumienia zasad, na których opiera się wiele konstrukcji architektonicznych i inżynieryjnych. W tym artykule omówimy szczegółowo definicje, własności oraz zastosowania tych typów kątów.

Kąty Przyległe: Definicja i Własności

Czym są kąty przyległe?

Kąty przyległe to dwa kąty, które mają wspólne ramię i wspólny wierzchołek, a ich wnętrza nie przecinają się. Innymi słowy, kąty te "stykają się" ze sobą, tworząc jedną linię prostą. Najważniejszą cechą kątów przyległych jest to, że ich suma miar wynosi 180 stopni. Nazywamy je również kątami liniowymi, ponieważ tworzą linię prostą.

Własności kątów przyległych

Podstawową własnością kątów przyległych jest ich suma miar równa 180 stopni. Można to zapisać jako:

α + β = 180°

Gdzie α i β to miary dwóch kątów przyległych. Ta prosta zależność pozwala na obliczanie miar kątów, jeżeli znana jest miara jednego z nich. Na przykład, jeżeli jeden z kątów przyległych ma miarę 60 stopni, to drugi kąt musi mieć miarę 120 stopni (180° - 60° = 120°).

Przykłady kątów przyległych w życiu codziennym

Kąty przyległe można zaobserwować w wielu aspektach życia codziennego. Przykłady obejmują:

Zegar: Kąt między wskazówką godzinową a minutową, gdy wskazówki tworzą linię prostą.
Drzwi: Kąt między drzwiami a futryną, gdy drzwi są częściowo otwarte i tworzą linię prostą z futryną.
Linie drogowe: Kąt między dwiema przecinającymi się liniami na drodze, jeśli tworzą one linię prostą.

Kąty Wierzchołkowe: Definicja i Własności

Czym są kąty wierzchołkowe?

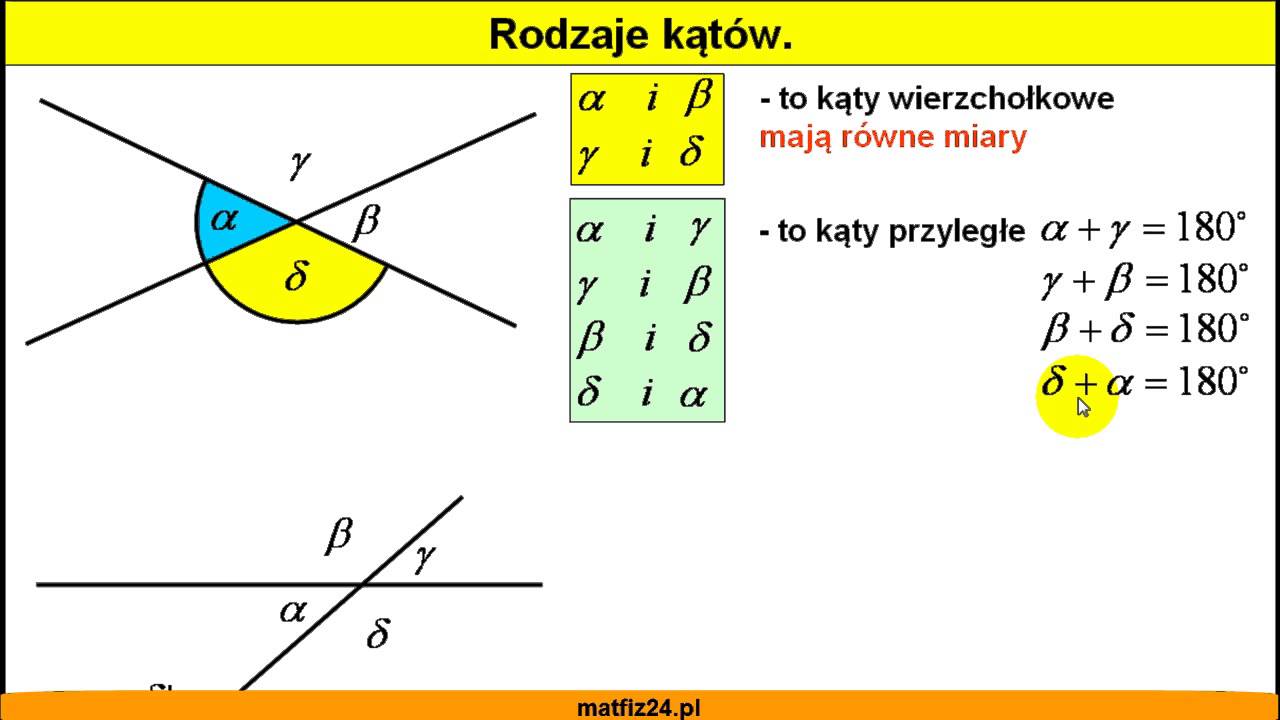
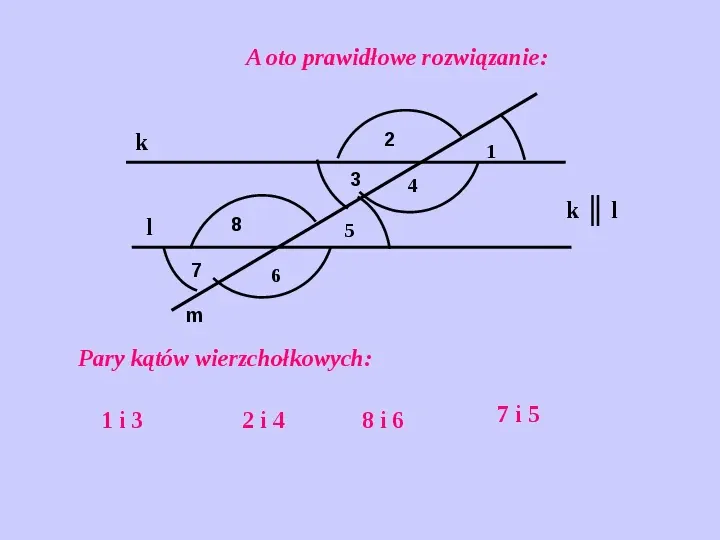
Kąty wierzchołkowe to para kątów, które powstają w wyniku przecięcia się dwóch prostych. Kąty te mają wspólny wierzchołek, ale nie mają wspólnych ramion. Charakteryzują się tym, że są równych miar. To jedna z najważniejszych własności kątów wierzchołkowych.

Własności kątów wierzchołkowych

Najważniejszą i definiującą własnością kątów wierzchołkowych jest ich równość miar. Można to zapisać jako:

α = γ oraz β = δ

Gdzie α i γ to jedna para kątów wierzchołkowych, a β i δ to druga para kątów wierzchołkowych utworzonych przez przecięcie dwóch prostych. Dzięki tej własności, znajomość miary jednego z kątów wierzchołkowych natychmiastowo implikuje znajomość miary jego pary.

Przykłady kątów wierzchołkowych w życiu codziennym

Podobnie jak w przypadku kątów przyległych, kąty wierzchołkowe są powszechnie spotykane w różnych sytuacjach. Przykłady obejmują:

Skrzyżowania drogowe: Kąty utworzone przez przecinające się ulice.
Nożyczki: Kąty między ostrzami nożyczek w punkcie ich połączenia.
Ramy okienne: Kąty utworzone przez krzyżujące się listwy ramy okiennej.

Zależności Między Kątami Przyległymi i Wierzchołkowymi

Ważne jest, aby zrozumieć, jak kąty przyległe i wierzchołkowe mogą współistnieć i wpływać na siebie. Rozważmy sytuację, w której dwie proste przecinają się, tworząc zarówno kąty wierzchołkowe, jak i przyległe.

Jeśli kąt α i kąt β są przyległe, to α + β = 180°. Jeśli kąt α i kąt γ są wierzchołkowe, to α = γ. Możemy wykorzystać te zależności do rozwiązywania problemów, w których mamy do czynienia z kombinacją tych typów kątów. Na przykład, jeśli wiemy, że kąt α ma miarę 50 stopni, to wiemy, że kąt γ (wierzchołkowy do α) również ma 50 stopni, a kąt β (przyległy do α) ma 130 stopni (180° - 50° = 130°).

Zastosowania w Geometrii i Architekturze

Zrozumienie własności kątów przyległych i wierzchołkowych ma praktyczne zastosowanie w wielu dziedzinach, w tym w geometrii, architekturze, inżynierii i projektowaniu graficznym. W geometrii, znajomość tych kątów pozwala na dowodzenie twierdzeń i rozwiązywanie problemów dotyczących trójkątów, czworokątów i innych figur geometrycznych.

W architekturze i inżynierii, te koncepcje są wykorzystywane do projektowania stabilnych i estetycznych struktur. Na przykład, architekci używają wiedzy o kątach do projektowania budynków, mostów i innych konstrukcji, które są zarówno funkcjonalne, jak i wizualnie atrakcyjne. Przykładem może być konstrukcja dachu, gdzie kąty nachylenia belek muszą być precyzyjnie obliczone, aby zapewnić wytrzymałość i stabilność całej struktury. W projektowaniu mostów, kąty między elementami konstrukcyjnymi są kluczowe dla rozkładu obciążeń i zapewnienia bezpieczeństwa użytkowników.

W projektowaniu graficznym, kąty i proporcje odgrywają ważną rolę w tworzeniu wizualnie atrakcyjnych i efektywnych projektów. Graficy używają wiedzy o kątach do tworzenia kompozycji, które są zarówno estetyczne, jak i funkcjonalne.

Przykładowe Zadania i Rozwiązania

Aby lepiej zrozumieć, jak stosować wiedzę o kątach przyległych i wierzchołkowych, rozważmy kilka przykładowych zadań:

Zadanie 1: Dwa kąty przyległe mają się do siebie jak 2:3. Oblicz miary tych kątów.
Rozwiązanie: Niech kąt α = 2x i kąt β = 3x. Ponieważ są przyległe, 2x + 3x = 180°. Zatem 5x = 180°, a x = 36°. Stąd α = 2 * 36° = 72°, a β = 3 * 36° = 108°.
Zadanie 2: Dwie proste przecinają się. Jeden z kątów wierzchołkowych ma miarę 45°. Oblicz miary pozostałych kątów.
Rozwiązanie: Kąt wierzchołkowy do danego kąta również ma miarę 45°. Kąt przyległy do kąta 45° ma miarę 180° - 45° = 135°. Kąt wierzchołkowy do kąta 135° również ma miarę 135°.
Zadanie 3: Kąt α ma miarę 60 stopni. Kąt β jest przyległy do kąta α, a kąt γ jest wierzchołkowy do kąta β. Oblicz miarę kąta γ.
Rozwiązanie: Kąt β (przyległy do α) ma miarę 180° - 60° = 120°. Kąt γ (wierzchołkowy do β) również ma miarę 120°.

Podsumowanie i Wnioski

Kąty przyległe i kąty wierzchołkowe to podstawowe, ale niezwykle istotne pojęcia w geometrii. Ich znajomość i umiejętność wykorzystywania ich własności jest kluczowa dla rozwiązywania problemów geometrycznych i zrozumienia zasad, na których opierają się liczne konstrukcje i projekty.

Zarówno w architekturze, inżynierii, jak i w życiu codziennym, te kąty odgrywają ważną rolę. Rozumienie ich właściwości pozwala na lepsze zrozumienie otaczającego nas świata i podejmowanie bardziej świadomych decyzji. Zachęcamy do dalszego zgłębiania wiedzy z zakresu geometrii i wykorzystywania zdobytych umiejętności w praktyce.

Pamiętaj: Ćwiczenie czyni mistrza! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zasady geometrii i tym łatwiej będzie Ci rozwiązywać bardziej złożone problemy.