Katy 30 60 90 W Trojkacie

Zastanawiałeś się kiedyś, dlaczego niektóre zadania z geometrii wydają się być prostsze od innych? Być może to zasługa magicznych trójkątów – a konkretnie, trójkąta o kątach 30, 60 i 90 stopni. Niejeden uczeń (i niejeden inżynier!) zmaga się z obliczeniami związanymi z długościami boków w trójkątach prostokątnych. Ale ten jeden, konkretny trójkąt kryje w sobie pewne ułatwienia, które znacznie upraszczają sprawę. Zatem, jak to działa i dlaczego warto o tym wiedzieć?

Wyobraź sobie, że próbujesz zaprojektować rampę dla wózków inwalidzkich. Kąt nachylenia jest kluczowy, prawda? Zbyt stromy – i rampa staje się bezużyteczna. Zbyt płaski – i zajmuje zbyt dużo miejsca. Wykorzystując właściwości trójkąta 30-60-90, możesz precyzyjnie obliczyć długość rampy i wysokość, jaką musi pokonać, znając tylko jeden z tych wymiarów. To nie tylko teoria z podręcznika – to realna pomoc w życiu codziennym. Podobnie, w budownictwie, podczas wznoszenia konstrukcji dachowych, ten trójkąt staje się niezastąpionym narzędziem.

Co sprawia, że trójkąt 30-60-90 jest wyjątkowy?

Sedno sprawy tkwi w specyficznych proporcjach pomiędzy długościami jego boków. To one umożliwiają nam szybkie i łatwe obliczenia. Ale zanim przejdziemy do wzorów, zrozummy, skąd się one biorą.

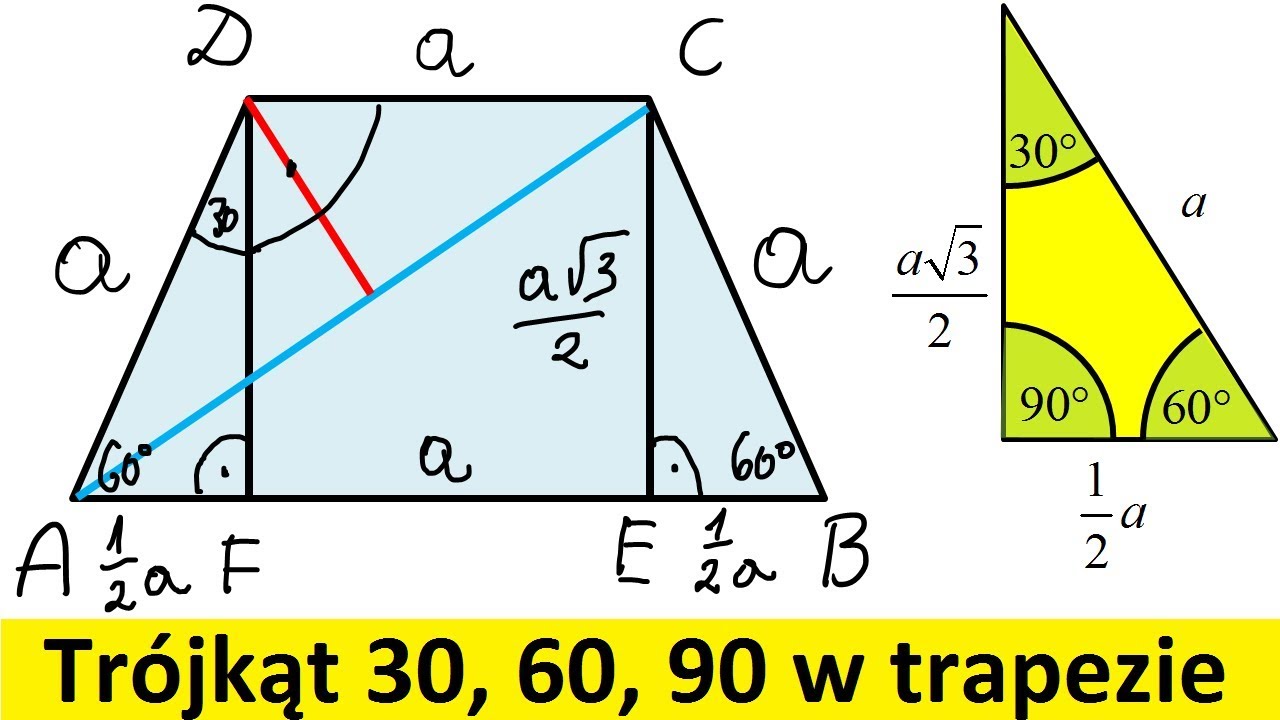
Krótsza przyprostokątna (naprzeciwko kąta 30 stopni): Nazwijmy ją "a".
Dłuższa przyprostokątna (naprzeciwko kąta 60 stopni): Jest równa a√3.
Przeciwprostokątna (naprzeciwko kąta 90 stopni): Jest równa 2a.

Zapamiętaj te relacje: a, a√3, 2a. Wiedząc, że krótsza przyprostokątna ma długość "a", możesz natychmiast wyznaczyć długość pozostałych boków. I odwrotnie: znając długość przeciwprostokątnej, możesz obliczyć długość krótszej przyprostokątnej (dzieląc długość przeciwprostokątnej przez 2) a następnie, długość dłuższej przyprostokątnej.

Przykłady praktyczne:

Przykład 1: Załóżmy, że krótsza przyprostokątna (a) ma długość 5 cm. Wtedy:

Dłuższa przyprostokątna = 5√3 cm
Przeciwprostokątna = 2 * 5 = 10 cm

Przykład 2: Załóżmy, że przeciwprostokątna ma długość 12 cm. Wtedy:

Krótsza przyprostokątna (a) = 12 / 2 = 6 cm
Dłuższa przyprostokątna = 6√3 cm

Skąd się to bierze? Dowód geometryczny

Możesz się zastanawiać, skąd właściwie wzięły się te proporcje. Otóż, trójkąt 30-60-90 to "połowa" trójkąta równobocznego. Wyobraź sobie trójkąt równoboczny o boku długości 2a. Jeśli przetniesz go na pół wzdłuż wysokości, otrzymasz dwa identyczne trójkąty 30-60-90. Wysokość trójkąta równobocznego stanowi dłuższą przyprostokątną trójkąta 30-60-90, a jej długość wynosi a√3 (co wynika z twierdzenia Pitagorasa).

Czy zawsze muszę pamiętać wzory? Kontrargumenty i alternatywy

Niektórzy twierdzą, że zapamiętywanie wzorów jest zbędne i zawsze można skorzystać z twierdzenia Pitagorasa lub funkcji trygonometrycznych (sinus, cosinus, tangens). To prawda. Jednak, w przypadku trójkąta 30-60-90 znajomość proporcji znacznie przyspiesza rozwiązywanie zadań. Zamiast mozolnie obliczać wartości sinusa i cosinusa dla kątów 30 i 60 stopni, możesz od razu zastosować odpowiednią proporcję. Poza tym, w niektórych sytuacjach (np. na egzaminach, gdzie czas jest ograniczony) szybsze rozwiązywanie zadań ma ogromne znaczenie. Znajomość tych proporcji to po prostu narzędzie, które możesz wykorzystać, gdy jest to najefektywniejsze.

Oczywiście, jeśli zapomnisz wzoru, twierdzenie Pitagorasa zawsze przyjdzie z pomocą! Pamiętaj, że a² + b² = c², gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej. Możesz również skorzystać z definicji funkcji trygonometrycznych: sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = √3/3, sin(60°) = √3/2, cos(60°) = 1/2, tan(60°) = √3.

Jak efektywnie zapamiętać i stosować proporcje?

Kluczem do sukcesu jest praktyka. Rozwiąż jak najwięcej zadań z wykorzystaniem trójkąta 30-60-90. Możesz:

Zacząć od prostych przykładów, gdzie znasz długość jednej strony i musisz obliczyć pozostałe.
Przechodzić do bardziej złożonych zadań, gdzie trójkąt 30-60-90 jest elementem większej figury geometrycznej.
Stosować wizualizacje: rysuj trójkąty 30-60-90 i oznaczaj długości boków.
Używać mnemotechnik: spróbuj wymyślić własne skojarzenia, które pomogą Ci zapamiętać proporcje.

Pamiętaj, że regularność jest ważniejsza niż intensywność. Krótkie, ale częste sesje ćwiczeń przyniosą lepsze efekty niż długie, sporadyczne zakuwanie.

Trójkąt 30-60-90 w życiu zawodowym

Jak już wspomniano, trójkąt 30-60-90 znajduje zastosowanie w wielu dziedzinach, takich jak:

Architektura i budownictwo: projektowanie dachów, ramp, schodów.
Inżynieria: obliczanie naprężeń w konstrukcjach, projektowanie maszyn.
Grafika komputerowa i gry: modelowanie trójwymiarowych obiektów, obliczanie perspektywy.
Nawigacja: wyznaczanie odległości i kątów.

Nawet jeśli nie planujesz kariery w tych dziedzinach, zrozumienie zasad geometrii, w tym właściwości trójkąta 30-60-90, rozwija Twoje umiejętności logicznego myślenia i rozwiązywania problemów, które są przydatne w każdej dziedzinie życia.

Podsumowanie i wnioski

Trójkąt 30-60-90 to nie tylko abstrakcyjna figura geometryczna, ale przede wszystkim praktyczne narzędzie, które ułatwia rozwiązywanie wielu problemów. Znajomość proporcji między długościami jego boków pozwala na szybkie i efektywne obliczenia, co jest szczególnie przydatne w architekturze, budownictwie, inżynierii i wielu innych dziedzinach. Choć można korzystać z twierdzenia Pitagorasa lub funkcji trygonometrycznych, znajomość proporcji w trójkącie 30-60-90 znacznie przyspiesza pracę.

Kluczem do opanowania tej wiedzy jest regularna praktyka i rozwiązywanie zadań. Nie bój się eksperymentować i szukać własnych sposobów na zapamiętanie proporcji. Pamiętaj, że geometria to nie tylko zbiór wzorów, ale przede wszystkim logiczne myślenie i kreatywność.

A teraz, zastanów się, w jakiej sytuacji w Twoim życiu mógłbyś wykorzystać wiedzę o trójkącie 30-60-90? Może przy projektowaniu własnego ogrodu, budowie domku dla ptaków, albo po prostu, rozwiązując zagadkę logiczną? Spróbuj! Zdziwisz się, jak wiele zastosowań może mieć ta prosta, ale potężna figura geometryczna. Czy podejmiesz wyzwanie?