Kąt Większy Od Kąta Półpełnego A Mniejszy Od Kąta Pełnego

Zacznijmy naszą podróż w fascynujący świat geometrii, skupiając się na kątach, które wykraczają poza standardowe definicje i dają nam nowe perspektywy na przestrzeń. Mówimy tu o kątach większych od kąta półpełnego, a mniejszych od kąta pełnego. Przygotujcie się na ekscytującą przygodę, podczas której odkryjemy ich cechy, zastosowania i sposoby mierzenia!

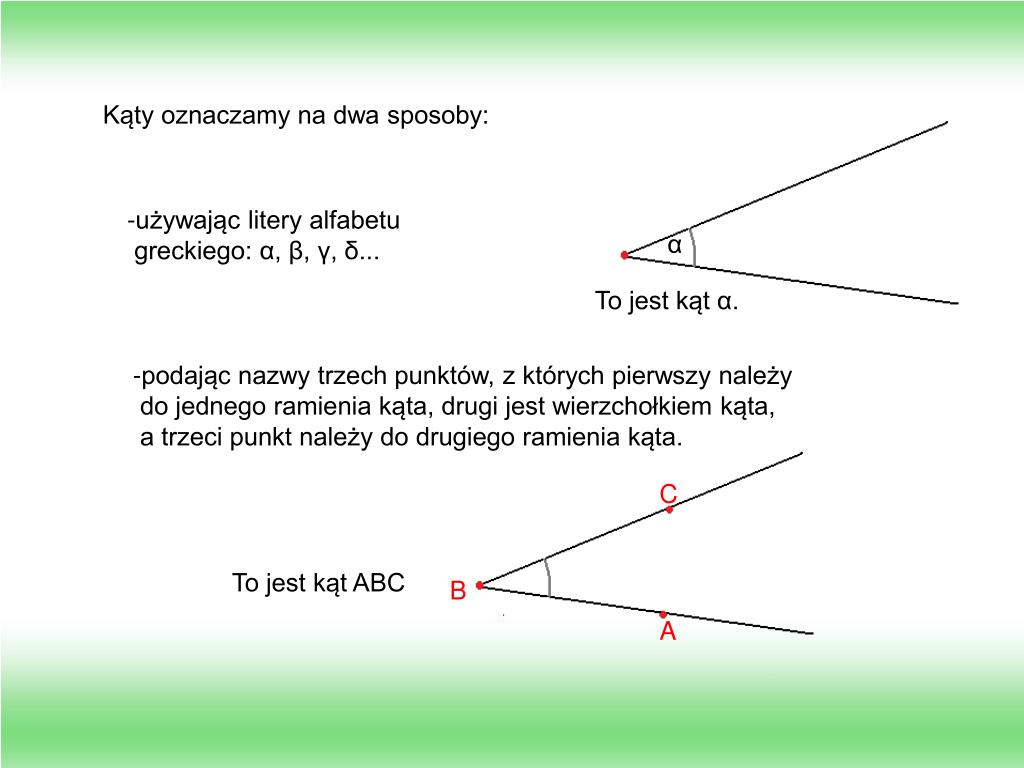
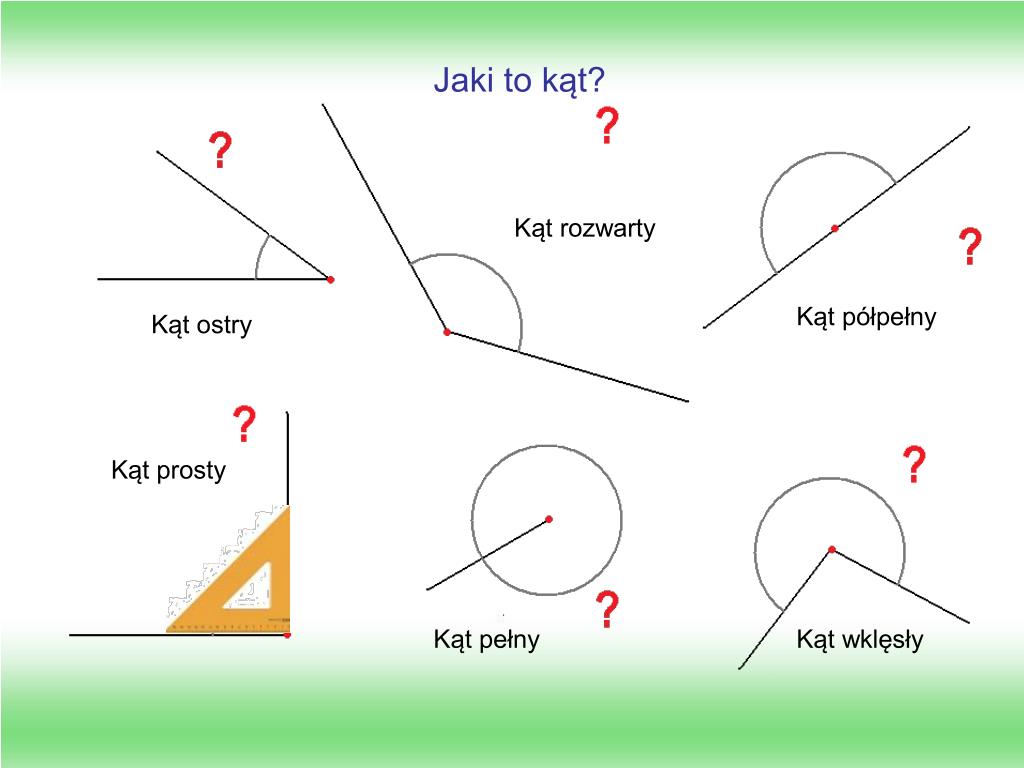
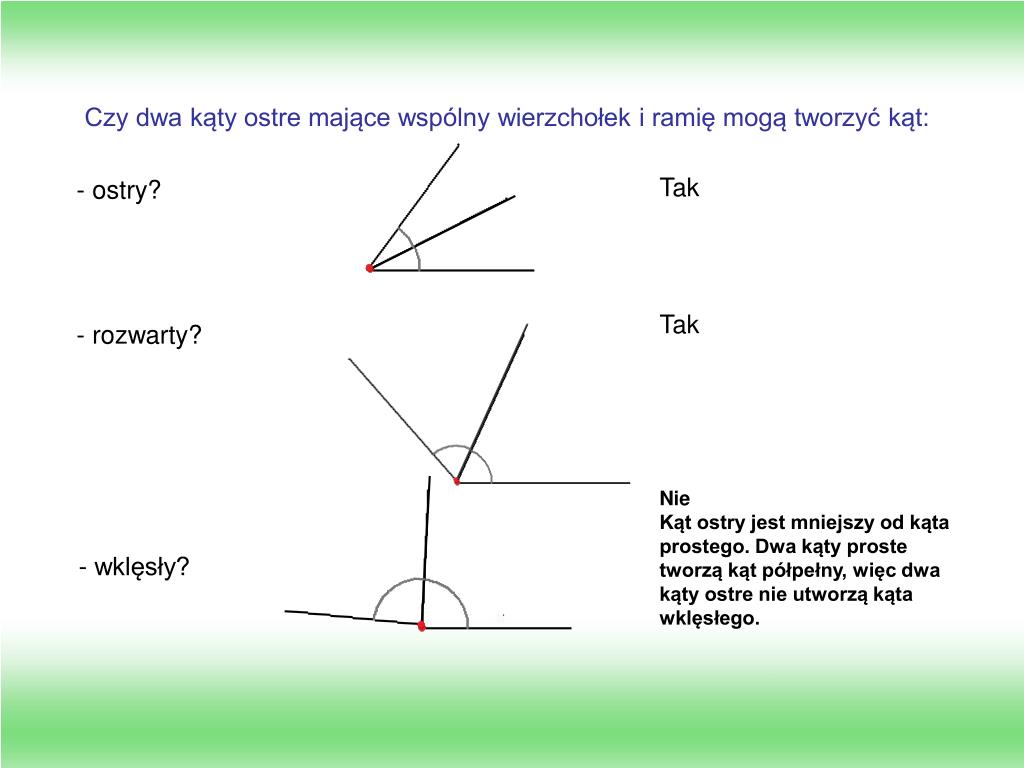
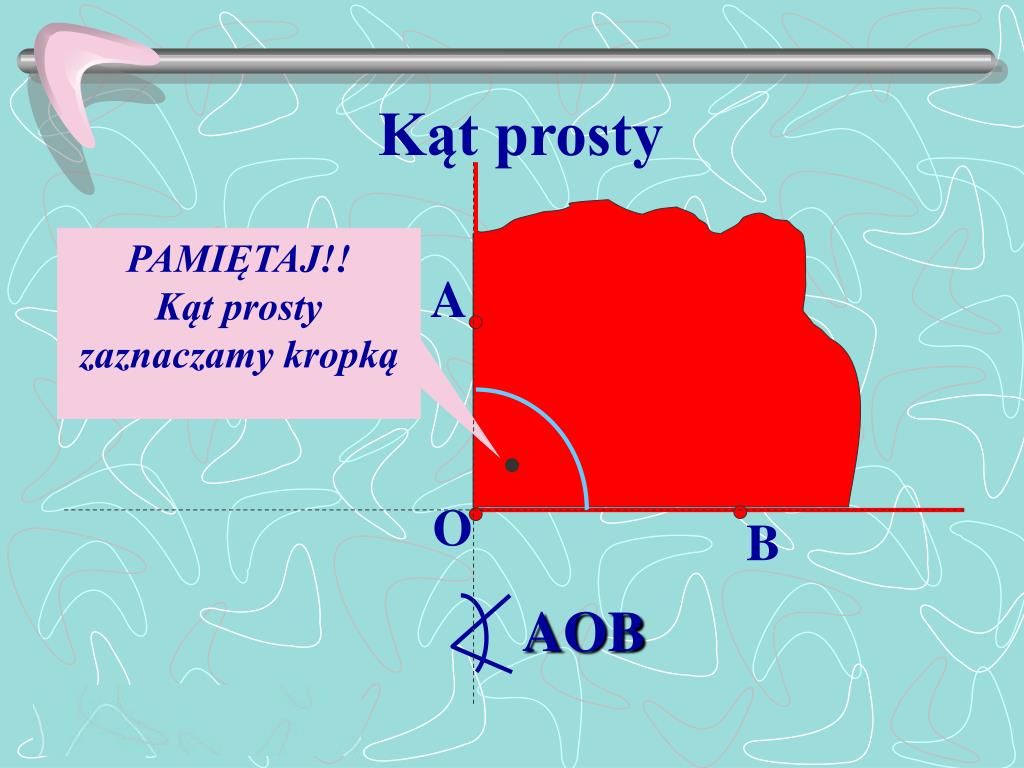
Zanim zagłębimy się w sedno sprawy, przypomnijmy sobie podstawowe definicje kątów, które pomogą nam zrozumieć, czym tak naprawdę są kąty większe od kąta półpełnego, a mniejsze od kąta pełnego. Kąt ostry to kąt mniejszy niż 90 stopni, kąt prosty ma dokładnie 90 stopni, a kąt rozwarty mieści się między 90 a 180 stopniami. Kąt półpełny, jak sama nazwa wskazuje, ma 180 stopni i tworzy linię prostą. Z kolei kąt pełny ma 360 stopni, co oznacza pełny obrót dookoła punktu.

Teraz wyobraźmy sobie kąt, który jest większy niż kąt półpełny (180 stopni). To znaczy, że wychodzi poza linię prostą, ale nie dochodzi jeszcze do pełnego okręgu (360 stopni). To właśnie ten specyficzny zakres definiuje kąt, którym się zajmujemy.

Nazwijmy go dla przejrzystości kątem "niestandardowym". Kąt niestandardowy, choć nie ma formalnej, powszechnie używanej nazwy, odgrywa istotną rolę w wielu dziedzinach, od matematyki po sztukę i architekturę. Zrozumienie jego właściwości pozwala nam lepiej interpretować otaczający nas świat.

Rozważmy na przykład wskazówki zegara. O godzinie siódmej wskazówka minutowa i godzinowa tworzą kąt niestandardowy. Podobnie, rozchylenie wachlarza, który jest otwarty bardziej niż do połowy, ale nie jest jeszcze całkowicie rozłożony, również tworzy kąt niestandardowy.

Pomiar Kątów Niestandardowych

Do mierzenia kątów niestandardowych używamy tych samych narzędzi, co do mierzenia innych kątów, czyli kątomierza. Ważne jest jednak, aby pamiętać o tym, że kątomierz zazwyczaj mierzy kąty do 180 stopni. W przypadku kątów niestandardowych mamy dwie możliwości.

Po pierwsze, możemy bezpośrednio zmierzyć mniejszy kąt, który "dopełnia" nasz kąt niestandardowy do pełnego okręgu. Następnie odejmujemy wartość tego kąta od 360 stopni, aby uzyskać miarę kąta niestandardowego. Przykładowo, jeśli zmierzyliśmy kąt "dopełniający" i okazało się, że ma on 60 stopni, to kąt niestandardowy ma miarę 360 - 60 = 300 stopni.

Po drugie, możemy skorzystać z kątomierza, dodając do 180 stopni (czyli kąta półpełnego) wartość, o którą nasz kąt niestandardowy "wychodzi" poza prostą linię. Przykładowo, jeśli nasz kąt wyraźnie przekracza linię prostą, a mierzymy to dodatkowe "wyjście" na 120 stopni, to nasz kąt niestandardowy ma miarę 180 + 120 = 300 stopni.

Obie metody prowadzą do tego samego wyniku, a wybór zależy od preferencji i konkretnych warunków pomiaru.

Warto również pamiętać, że w niektórych przypadkach, zwłaszcza w kontekście programowania grafiki komputerowej, kąty są często reprezentowane w radianach. Kąt pełny (360 stopni) odpowiada 2π radianów. Zatem, aby przeliczyć miarę kąta niestandardowego ze stopni na radiany, musimy pomnożyć jego wartość w stopniach przez π/180. Przykładowo, kąt 300 stopni w radianach to (300 * π) / 180 = (5/3)π radianów.

Zastosowania Kątów Niestandardowych

Kąty niestandardowe, choć na pierwszy rzut oka mogą wydawać się jedynie abstrakcyjnym konceptem matematycznym, znajdują szerokie zastosowanie w wielu dziedzinach życia.

W grafice komputerowej, kąty niestandardowe są niezbędne do opisywania obrotów obiektów w przestrzeni trójwymiarowej. Wyobraźmy sobie, że chcemy obrócić model 3D o 270 stopni wokół osi pionowej. Użycie kąta niestandardowego (270 stopni) pozwala nam precyzyjnie zdefiniować ten obrót i uzyskać pożądany efekt wizualny.

W robotyce, kąty niestandardowe są wykorzystywane do programowania ruchów robotów, zwłaszcza tych, które wykonują skomplikowane operacje, takie jak spawanie, malowanie czy montaż elementów. Precyzyjne określenie kątów obrotu stawów robota jest kluczowe dla zapewnienia prawidłowego i efektywnego działania urządzenia.

W nawigacji morskiej i lotniczej, kąty niestandardowe mogą być używane do opisywania kursów statków i samolotów. Choć zazwyczaj korzysta się z kompasu i azymutu (kąta mierzonego od północy), w niektórych sytuacjach, zwłaszcza przy analizie danych z radarów i sonarów, kąty niestandardowe mogą okazać się przydatne.

W astronomii, kąty niestandardowe mogą pojawiać się przy analizie trajektorii ciał niebieskich, takich jak komety czy asteroidy. Zrozumienie geometrii orbit i relacji kątowych między różnymi obiektami w przestrzeni kosmicznej jest kluczowe dla przewidywania przyszłych zdarzeń, takich jak zbliżenia planet czy przeloty komet w pobliżu Ziemi.

Ponadto, kąty niestandardowe znajdują zastosowanie w mechanice, fizyce i innych dziedzinach nauki i techniki. Przykładowo, w analizie naprężeń w konstrukcjach budowlanych, kąty między różnymi elementami konstrukcyjnymi mogą być mierzone i analizowane, aby zapewnić bezpieczeństwo i stabilność budowli.

Podsumowując, choć kąty niestandardowe nie są tak powszechnie omawiane jak kąty ostre, proste czy rozwarte, stanowią ważny element naszego zrozumienia geometrii i mają liczne praktyczne zastosowania w różnych dziedzinach. Zrozumienie ich właściwości i sposobów mierzenia pozwala nam lepiej interpretować i modelować otaczający nas świat.

Poznawanie świata kątów to fascynująca podróż, która pozwala nam dostrzec matematykę w najróżniejszych aspektach naszego życia. Kąty niestandardowe, choć na pierwszy rzut oka mogą wydawać się abstrakcją, w rzeczywistości odgrywają istotną rolę w wielu dziedzinach nauki i techniki.

Pamiętajmy, że matematyka to nie tylko zbiór wzorów i definicji, ale przede wszystkim sposób na zrozumienie i opisanie świata, który nas otacza. A im lepiej rozumiemy ten świat, tym lepiej możemy go kształtować i rozwijać.

Odkrywajmy więc dalej tajemnice geometrii i pozwólmy, aby fascynacja matematyką towarzyszyła nam przez całe życie!