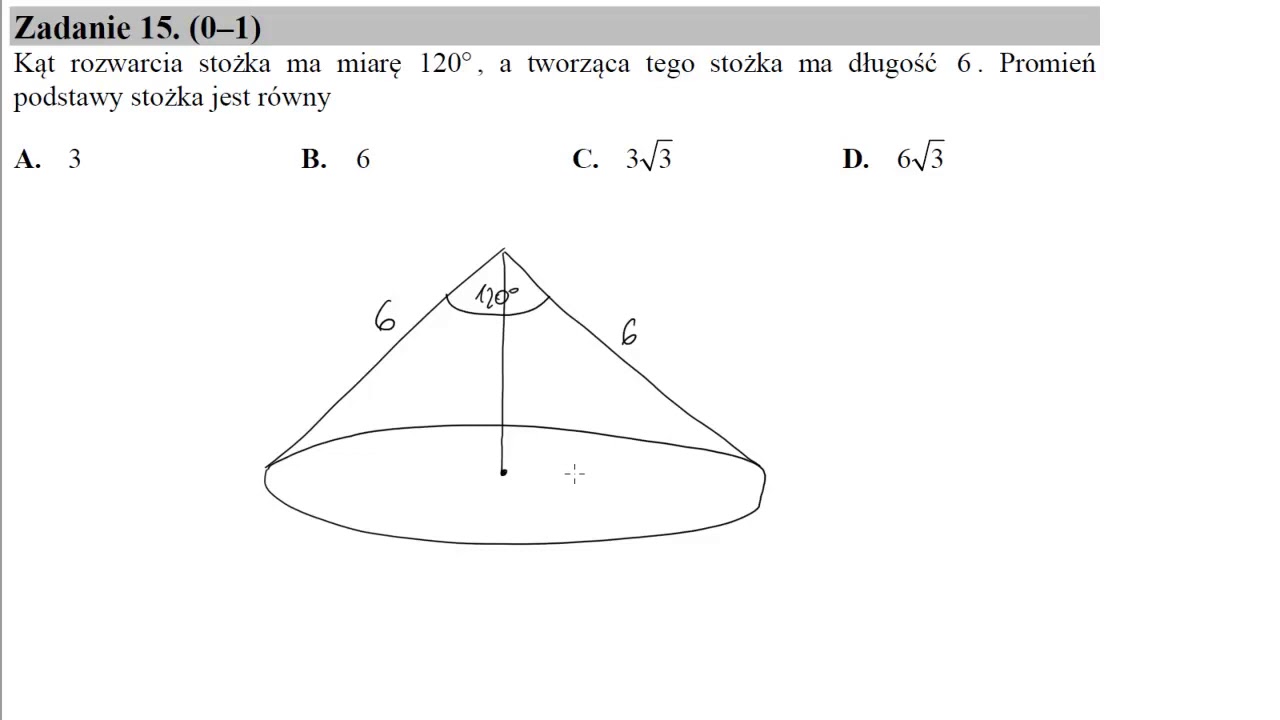
Kat Rozwarcia Stozka Ma Miare 120

Czy kiedykolwiek zastanawiałeś się, jak wyglądają stożki, których rozwarcie kąta u szczytu wynosi 120 stopni? Może wydawać się to abstrakcyjne, ale zrozumienie geometrii tych figur ma praktyczne zastosowanie w wielu dziedzinach, od architektury po inżynierię. W tym artykule przyjrzymy się bliżej stożkom o rozwartości 120 stopni, zrozumiemy ich właściwości i zobaczymy, gdzie możemy je spotkać w otaczającym nas świecie. Artykuł skierowany jest do osób zainteresowanych matematyką, inżynierią, architekturą, a także do uczniów i studentów, którzy chcą poszerzyć swoją wiedzę z zakresu geometrii.

Wprowadzenie do Stożków

Zacznijmy od podstaw. Stożek to bryła obrotowa powstająca przez obrót trójkąta prostokątnego wokół jednej z jego przyprostokątnych. Charakteryzuje się on podstawą w kształcie koła i powierzchnią boczną zbiegającą się w jednym punkcie – wierzchołku. Kąt rozwarcia stożka to kąt między dwiema prostymi przechodzącymi przez wierzchołek stożka i dotykającymi okręgu podstawy.

Rozważmy stożek prosty (czyli taki, w którym wierzchołek leży prosto nad środkiem podstawy). Jego właściwości zależą od kilku kluczowych parametrów:

• Promień podstawy (r): Odległość od środka podstawy do dowolnego punktu na okręgu podstawy.
• Wysokość stożka (h): Odległość od wierzchołka do środka podstawy.
• Tworząca stożka (l): Odległość od wierzchołka do dowolnego punktu na okręgu podstawy.
• Kąt rozwarcia (α): Kąt między dwiema tworzącymi leżącymi na przeciwległych krańcach podstawy i przechodzącymi przez wierzchołek. W naszym przypadku α = 120 stopni.

Związek między parametrami stożka

Parametry stożka są ze sobą powiązane za pomocą zależności trygonometrycznych. W przypadku stożka prostego o kącie rozwarcia α, promień podstawy *r*, wysokość *h* i tworząca *l* spełniają następujące równania:

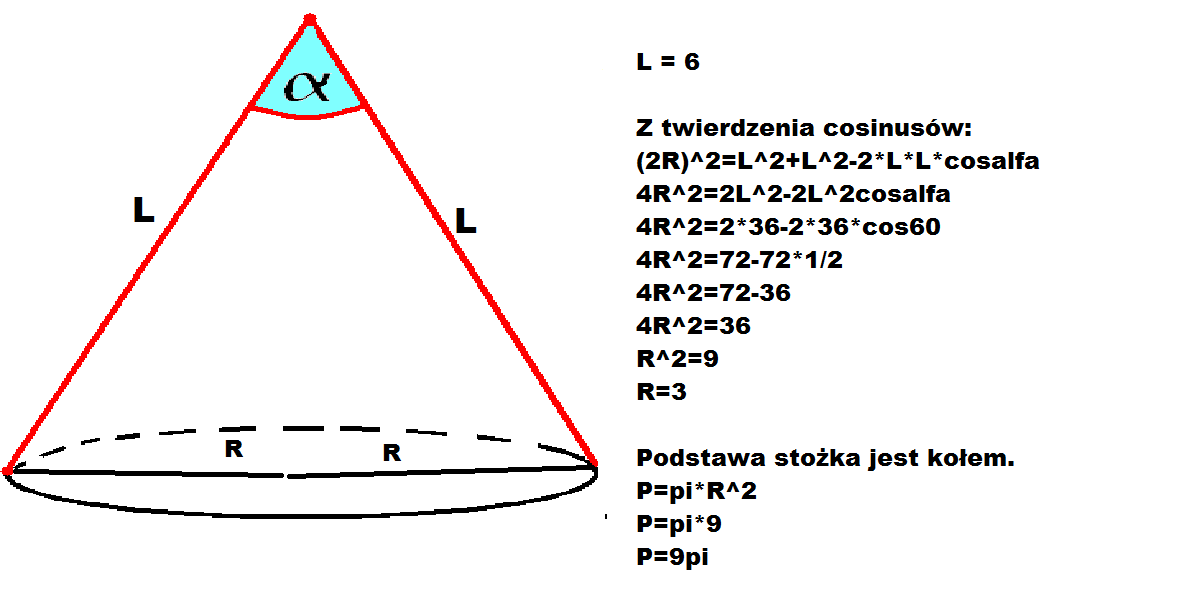
• tan(α/2) = r/h (W naszym przypadku tan(60°) = r/h)
• l² = r² + h² (Z twierdzenia Pitagorasa)

Wiedząc, że α = 120 stopni, możemy stwierdzić, że tan(α/2) = tan(60°) = √3. Zatem, dla stożka o rozwartości 120 stopni, r = h√3. Oznacza to, że promień podstawy jest √3 razy większy od wysokości stożka.

Stożek o Kącie Rozwarcia 120 Stopni – Szczegółowa Analiza

Skupmy się teraz na specyfice stożka o kącie rozwarcia 120 stopni. Jak już ustaliliśmy, relacja między promieniem podstawy a wysokością takiego stożka jest stała: r = h√3.

Powierzchnia i Objętość

Znając tę relację, możemy wyrazić powierzchnię i objętość stożka o kącie rozwarcia 120 stopni w zależności od jednej zmiennej (np. wysokości h).

• Powierzchnia podstawy (P_p): P_p = πr² = π(h√3)² = 3πh²
• Powierzchnia boczna (P_b): P_b = πrl. Z twierdzenia Pitagorasa, l = √(r² + h²) = √((h√3)² + h²) = √(3h² + h²) = √(4h²) = 2h. Zatem P_b = π(h√3)(2h) = 2√3πh²
• Powierzchnia całkowita (P_c): P_c = P_p + P_b = 3πh² + 2√3πh² = πh²(3 + 2√3)
• Objętość (V): V = (1/3)πr²h = (1/3)π(h√3)²h = (1/3)π(3h²)h = πh³

Zauważ, że objętość stożka o kącie rozwarcia 120 stopni zależy tylko od trzeciej potęgi jego wysokości. Dla porównania, powierzchnia całkowita zależy od kwadratu wysokości. To pokazuje, jak zmieniają się proporcje stożka wraz ze zmianą jego wymiarów.

Wyobraźnia przestrzenna

Wyobraź sobie stożek o kącie rozwarcia 120 stopni. Jest on stosunkowo "płaski", tzn. jego podstawa jest znacznie szersza niż jego wysokość. Kąt 60 stopni, który tworzy tworząca z wysokością, jest dość spory, co sprawia, że stożek wygląda na bardziej "rozłożysty" niż stożek o mniejszym kącie rozwarcia.

Gdzie Spotykamy Stożki o Kącie Rozwarcia Bliskim 120 Stopni?

Chociaż idealne stożki o kącie 120 stopni są rzadkością w naturalnym środowisku, możemy znaleźć zbliżone kształty w różnych dziedzinach:

• Architektura: Niektóre dachy i kopuły przybierają kształt zbliżony do stożka. Chociaż rzadko mają idealny kąt 120 stopni, ich kształt nawiązuje do idei stożka o szerokiej podstawie.
• Inżynieria: Elementy konstrukcyjne, takie jak dysze, lejki i niektóre rodzaje złączy, mogą wykorzystywać kształt stożka o kącie bliskim 120 stopni, aby optymalizować przepływ płynów lub gazów.
• Natura: Stożki lawy wulkanicznej, choć nieregularne, mogą w przybliżeniu przypominać stożek o szerokiej podstawie. Podobne kształty można zaobserwować w formacjach skalnych powstałych w wyniku erozji.
• Projektowanie: Abażury lamp, elementy dekoracyjne, a nawet niektóre naczynia kuchenne mogą mieć kształty oparte na stożku o kącie bliskim 120 stopni.

Ważne jest, aby pamiętać, że w praktyce rzadko spotykamy idealne kształty geometryczne. Częściej mamy do czynienia z przybliżeniami i wariacjami, które zachowują ogólną ideę stożka o danej rozwartości.

Praktyczne Zastosowania Wiedzy o Stożkach

Zrozumienie geometrii stożków, w tym tych o rozwartości 120 stopni, ma praktyczne zastosowanie w wielu dziedzinach:

• Obliczenia objętości i powierzchni: Inżynierowie i architekci wykorzystują wzory na objętość i powierzchnię stożków do projektowania konstrukcji, obliczania ilości materiałów i optymalizacji kształtów.
• Projektowanie optyczne: W optyce stożki są wykorzystywane do projektowania soczewek i reflektorów. Kąt rozwarcia stożka ma wpływ na sposób, w jaki światło jest skupiane lub rozpraszane.
• Modelowanie 3D: Stożki są podstawowym elementem w modelowaniu 3D. Umożliwiają tworzenie realistycznych kształtów i obiektów w wirtualnych środowiskach.
• Analiza numeryczna: W analizie numerycznej stożki mogą być wykorzystywane do aproksymacji bardziej złożonych kształtów, co ułatwia rozwiązywanie problemów inżynierskich i naukowych.

Na przykład, projektując lej, inżynier musi uwzględnić kąt rozwarcia, aby zapewnić efektywny przepływ cieczy. Zbyt mały kąt może powodować zatory, a zbyt duży może zmniejszyć wydajność. Wiedza o relacjach geometrycznych w stożku pozwala na optymalizację konstrukcji.

Podsumowanie i Wartość Dodana

W tym artykule przyjrzeliśmy się bliżej stożkowi o kącie rozwarcia 120 stopni. Zrozumieliśmy, jak relacja między promieniem podstawy a wysokością wpływa na jego proporcje. Nauczyliśmy się obliczać jego powierzchnię i objętość, a także zobaczyliśmy, gdzie możemy spotkać zbliżone kształty w otaczającym nas świecie.

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć geometrię stożków i docenić ich znaczenie w różnych dziedzinach. Wiedza o podstawowych kształtach geometrycznych, takich jak stożek, jest kluczowa dla rozwoju umiejętności analitycznych i rozwiązywania problemów inżynierskich i naukowych. Zachęcam do dalszego zgłębiania tajników geometrii i odkrywania, jak matematyka kształtuje nasz świat!

Pamiętaj, że matematyka nie jest abstrakcyjną nauką – to język, którym opisujemy i rozumiemy wszechświat. Im lepiej go znamy, tym lepiej rozumiemy świat wokół nas.