Kat Miedzy Przekatna Sciany Bocznej A Sasiednia Sciana Boczna

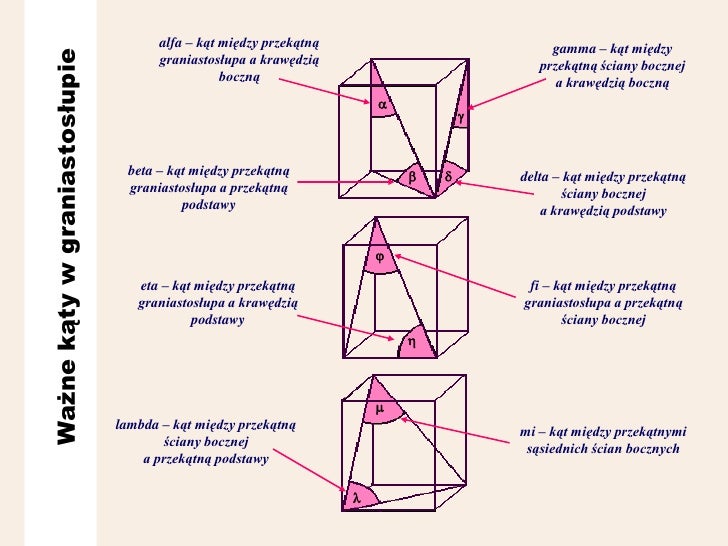
W geometrii przestrzennej, a konkretnie w zagadnieniach dotyczących graniastosłupów i ostrosłupów, często spotykamy się z problemami wymagającymi analizy relacji kątowych i odległości między różnymi elementami figury. Jednym z takich problemów jest określenie miary kąta pomiędzy przekątną ściany bocznej a sąsiednią ścianą boczną. Rozwiązanie tego typu zadania wymaga zrozumienia podstawowych zasad geometrii, w tym definicji kąta między prostą a płaszczyzną oraz umiejętności wykorzystywania twierdzenia Pitagorasa i funkcji trygonometrycznych.

Rozważmy graniastosłup prosty o podstawie będącej wielokątem. Wybierzmy jedną ze ścian bocznych i narysujmy jej przekątną. Następnie spójrzmy na ścianę boczną, która jest sąsiednia do wybranej. Naszym celem jest znalezienie kąta, jaki tworzy przekątna pierwszej ściany bocznej z drugą ścianą boczną.

Aby to zrobić, musimy znaleźć rzut tej przekątnej na płaszczyznę sąsiedniej ściany bocznej. Rzut ten będzie odcinkiem leżącym na tej płaszczyźnie, a kąt między przekątną a jej rzutem będzie szukanym kątem.

Kluczowym krokiem jest zrozumienie, jak skonstruować ten rzut. Wyobraźmy sobie, że z końca przekątnej ściany bocznej (punkt, który nie leży na sąsiedniej ścianie bocznej) prowadzimy prostą prostopadłą do płaszczyzny sąsiedniej ściany bocznej. Punkt przecięcia tej prostej z płaszczyzną ściany bocznej będzie końcem rzutu. Drugi koniec rzutu będzie punktem wspólnym przekątnej i sąsiedniej ściany bocznej.

Po skonstruowaniu rzutu, możemy utworzyć trójkąt prostokątny, którego wierzchołkami są: koniec przekątnej, koniec rzutu (czyli punkt przecięcia prostej prostopadłej z płaszczyzną ściany bocznej) oraz punkt wspólny przekątnej i sąsiedniej ściany bocznej. W tym trójkącie, przeciwprostokątną jest przekątna ściany bocznej, a jedną z przyprostokątnych jest rzut przekątnej na sąsiednią ścianę boczną. Szukany kąt jest kątem między przeciwprostokątną a przyprostokątną, czyli kątem między przekątną a jej rzutem.

Do obliczenia miary tego kąta możemy użyć funkcji trygonometrycznych, takich jak sinus, cosinus lub tangens. Wybór funkcji zależy od tego, jakie dane są nam znane. Jeśli znamy długość przekątnej i długość jej rzutu, możemy użyć cosinusa: cos(α) = (długość rzutu) / (długość przekątnej). Następnie, używając funkcji arcus cosinus (arccos), możemy obliczyć miarę kąta α.

Jeśli znamy długość odcinka łączącego koniec przekątnej z jej rzutem (czyli długość prostej prostopadłej do płaszczyzny ściany bocznej) oraz długość przekątnej, możemy użyć sinusa: sin(α) = (długość odcinka prostopadłego) / (długość przekątnej). Następnie, używając funkcji arcus sinus (arcsin), możemy obliczyć miarę kąta α.

Jeśli znamy długość odcinka łączącego koniec przekątnej z jej rzutem oraz długość rzutu, możemy użyć tangensa: tan(α) = (długość odcinka prostopadłego) / (długość rzutu). Następnie, używając funkcji arcus tangens (arctan), możemy obliczyć miarę kąta α.

W praktyce, często konieczne jest wykorzystanie twierdzenia Pitagorasa do obliczenia długości potrzebnych odcinków. Przykładowo, jeśli znamy wymiary graniastosłupa (długość krawędzi podstawy i wysokość), możemy obliczyć długość przekątnej ściany bocznej oraz długość odcinka łączącego koniec przekątnej z jej rzutem, a następnie użyć odpowiedniej funkcji trygonometrycznej do obliczenia miary kąta.

Analiza konkretnego przykładu – sześcian

Rozważmy sześcian o krawędzi długości a. Wybierzmy jedną ze ścian i jej przekątną. Długość tej przekątnej, zgodnie z twierdzeniem Pitagorasa, wynosi a√2. Teraz spójrzmy na sąsiednią ścianę boczną. Musimy znaleźć rzut przekątnej pierwszej ściany na drugą ścianę.

W przypadku sześcianu, rzut przekątnej na sąsiednią ścianę będzie po prostu krawędzią sześcianu, czyli odcinkiem o długości a. Możemy to zobaczyć, wyobrażając sobie prostą prostopadłą poprowadzoną z końca przekątnej (punktu nieleżącego na sąsiedniej ścianie) do płaszczyzny sąsiedniej ściany. Punkt przecięcia tej prostej z płaszczyzną będzie wierzchołkiem sześcianu, a odcinek łączący ten wierzchołek z punktem wspólnym przekątnej i sąsiedniej ściany będzie krawędzią sześcianu.

Teraz mamy trójkąt prostokątny, którego przeciwprostokątną jest przekątna ściany bocznej (długości a√2), a jedną z przyprostokątnych jest krawędź sześcianu (długości a). Możemy użyć cosinusa do obliczenia kąta α:

cos(α) = (długość rzutu) / (długość przekątnej) = a / (a√2) = 1 / √2 = √2 / 2

Zatem α = arccos(√2 / 2) = 45 stopni.

W tym przypadku kąt między przekątną ściany bocznej sześcianu a sąsiednią ścianą boczną wynosi 45 stopni.

Uogólnienie dla graniastosłupów prostych

Powyższy przykład dotyczył sześcianu, ale możemy uogólnić to rozumowanie dla innych graniastosłupów prostych. Kluczowe jest zrozumienie, jak skonstruować rzut przekątnej na sąsiednią ścianę i jak obliczyć długość tego rzutu oraz długość odcinka łączącego koniec przekątnej z jej rzutem.

W przypadku bardziej złożonych figur, takich jak graniastosłupy o podstawie będącej wielokątem innym niż kwadrat, obliczenia mogą być bardziej skomplikowane i mogą wymagać wykorzystania dodatkowych twierdzeń i wzorów z geometrii. Ważne jest, aby dokładnie przeanalizować geometrię figury i zidentyfikować odpowiednie trójkąty prostokątne, które pozwolą na obliczenie szukanego kąta.

Należy również pamiętać o tym, że kąt między przekątną ściany bocznej a sąsiednią ścianą boczną zależy od wymiarów graniastosłupa i może się różnić w zależności od kształtu podstawy i wysokości. Dlatego też, nie ma uniwersalnego wzoru na obliczenie tego kąta, a każde zadanie wymaga indywidualnego podejścia i analizy.

Podsumowując, znalezienie kąta między przekątną ściany bocznej a sąsiednią ścianą boczną w graniastosłupie prostym wymaga zrozumienia zasad geometrii przestrzennej, umiejętności konstruowania rzutów, wykorzystywania twierdzenia Pitagorasa i funkcji trygonometrycznych. Poprzez dokładną analizę geometrii figury i identyfikację odpowiednich trójkątów prostokątnych, możemy skutecznie rozwiązywać tego typu zadania.