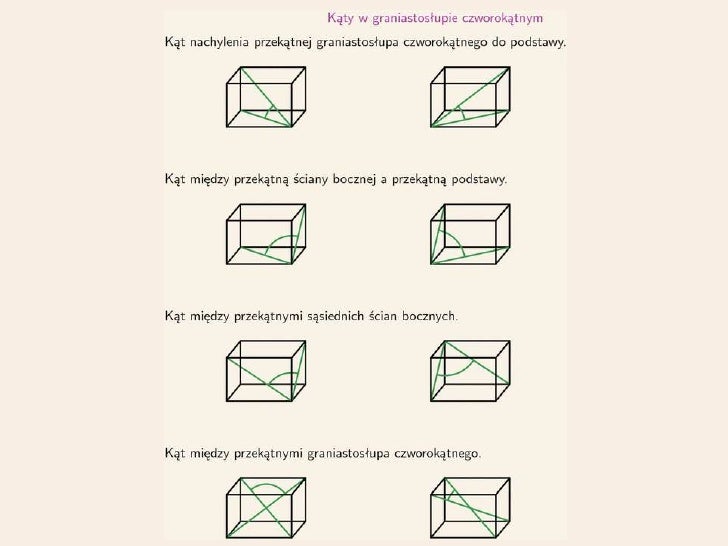
Kąt Między Przekątną Graniastosłupa A ścianą Boczną

Okej, spróbujmy rozgryźć kąt między przekątną graniastosłupa a jego ścianą boczną! Brzmi trochę strasznie, ale obiecuję, że krok po kroku zrozumiemy, o co chodzi. Potrzebujesz tylko trochę wyobraźni i podstawowej wiedzy z geometrii.

Na początek, zdefiniujmy sobie, o czym mówimy. Podzielmy problem na kilka mniejszych kawałków:

• Graniastosłup: Wyobraź sobie pudełko, ale niekoniecznie prostokątne. Graniastosłup to bryła, która ma dwie identyczne podstawy (na przykład trójkąty, kwadraty, pięciokąty, cokolwiek!), połączone ścianami bocznymi, które są równoległobokami (najczęściej prostokątami). Możemy mieć graniastosłup trójkątny, czworokątny, pięciokątny, itd. - w zależności od tego, jaki kształt ma podstawa. Pomyśl o tablicy czekolady Toblerone (graniastosłup trójkątny) albo pudełku z butami (graniastosłup czworokątny).

• Ściana boczna: To te "boki" graniastosłupa, które łączą dwie podstawy. Najczęściej są to prostokąty, ale ogólnie mogą być równoległobokami.

• Przekątna graniastosłupa: To odcinek łączący dwa wierzchołki graniastosłupa, które nie leżą na tej samej ścianie (ani na tej samej podstawie). Czyli przechodzi "przez wnętrze" graniastosłupa. Pomyśl o długiej, wykałaczce włożonej w pudełko z butami - musi przeciąć wnętrze pudełka, a nie tylko leżeć na jego dnie lub ścianie.

• Kąt: No dobrze, to już chyba wszyscy wiemy, co to kąt! To miara "rozwarcia" między dwiema prostymi, które przecinają się w jednym punkcie. Mierzymy go w stopniach (np. 30°, 90°, 180°).

Jak znaleźć ten kąt?

Okay, teraz kiedy mamy już zdefiniowane wszystkie elementy, możemy przejść do meritum sprawy. Jak znaleźć kąt między przekątną graniastosłupa a ścianą boczną?

1. Wyobraź sobie graniastosłup: Wybierzmy sobie prosty przykład - graniastosłup prosty czworokątny, czyli po prostu prostopadłościan (np. nasze pudełko z butami). Ułatwi to wizualizację.

2. Wybierz przekątną: Narysuj (lub wyobraź sobie) przekątną graniastosłupa. Pamiętaj, że musi ona łączyć wierzchołki leżące na różnych podstawach i różnych ścianach bocznych.

3. Wybierz ścianę boczną: Wybierz jedną ze ścian bocznych, która jest "blisko" wybranej przekątnej.

4. Znajdź rzut przekątnej na ścianę boczną: To kluczowy krok! Musimy znaleźć linię, która jest "cieniem" przekątnej na ścianie bocznej. Technicznie nazywamy to rzutem prostokątnym przekątnej na ścianę boczną. Wyobraź sobie, że świecisz latarką prostopadle na ścianę boczną, a przekątna rzuca cień. Ten cień to właśnie rzut. W przypadku prostopadłościanu, rzut przekątnej graniastosłupa na ścianę boczną, będzie przekątną tej ściany.

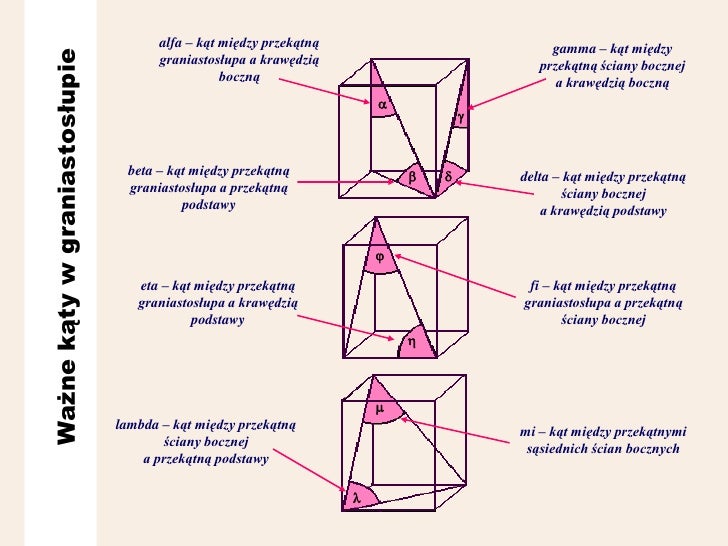
5. Zdefiniuj kąt: Kąt, którego szukamy, to kąt między przekątną graniastosłupa (tą wyjściową) a jej rzutem na ścianę boczną.

6. Użyj trygonometrii: Teraz, mając te trzy linie (przekątną graniastosłupa, jej rzut na ścianę boczną i odcinek łączący koniec przekątnej z końcem jej rzutu) tworzymy trójkąt prostokątny! Możemy teraz użyć funkcji trygonometrycznych (sinus, cosinus, tangens) aby obliczyć kąt.

H2: Przykładowe obliczenia

Załóżmy, że mamy prostopadłościan o wymiarach a = 3 cm, b = 4 cm, c = 5 cm. Chcemy obliczyć kąt między przekątną graniastosłupa a ścianą o wymiarach b x c.

1. Długość przekątnej graniastosłupa (d): Możemy obliczyć ją ze wzoru: d = √(a² + b² + c²) = √(3² + 4² + 5²) = √(9 + 16 + 25) = √50 = 5√2 cm.

2. Długość przekątnej ściany bocznej (d_ściany): d_ściany = √(b² + c²) = √(4² + 5²) = √(16 + 25) = √41 cm.

3. Używamy cosinusa: Cosinus kąta (α) między przekątną graniastosłupa a jej rzutem (czyli przekątną ściany) jest równy ilorazowi długości rzutu (d_ściany) przez długość przekątnej graniastosłupa (d):

   cos(α) = d_ściany / d = √41 / (5√2)

4. Obliczamy kąt: Aby znaleźć kąt α, musimy użyć funkcji arcus cosinus (arccos) lub cos^-1 na kalkulatorze:

   α = arccos(√41 / (5√2)) ≈ arccos(0.9055) ≈ 25.15°

Więc kąt między przekątną graniastosłupa a ścianą boczną w tym przypadku wynosi około 25.15 stopni.

Kilka ważnych uwag:

• Wybór ściany bocznej: Kąt będzie inny, w zależności od tego, którą ścianę boczną wybierzemy. Przekątna graniastosłupa tworzy różne kąty z różnymi ścianami bocznymi.
• Graniastosłup prosty vs. pochyły: W przypadku graniastosłupa prostego (gdzie ściany boczne są prostopadłe do podstaw), obliczenia są prostsze, ponieważ rzut przekątnej na ścianę boczną jest łatwiejszy do wyobrażenia. W graniastosłupie pochyłym jest trochę trudniej, ale zasada jest ta sama - trzeba znaleźć rzut przekątnej na ścianę boczną.
• Trygonometria to podstawa: Musisz dobrze znać funkcje trygonometryczne (sinus, cosinus, tangens) i umieć je stosować w trójkątach prostokątnych. Jeśli masz z tym problemy, warto sobie to powtórzyć.

H2: Dlaczego to jest ważne?

Może się zastanawiasz, po co w ogóle zawracać sobie głowę obliczaniem kąta między przekątną graniastosłupa a ścianą boczną. Otóż, znajomość geometrii przestrzennej jest bardzo przydatna w wielu dziedzinach, takich jak:

• Architektura i budownictwo: Projektowanie budynków, mostów, dachów wymaga znajomości geometrii przestrzennej, aby zapewnić stabilność i wytrzymałość konstrukcji. Obliczanie kątów, odległości i powierzchni jest kluczowe.
• Inżynieria: Projektowanie maszyn, urządzeń, robotów wymaga precyzyjnych obliczeń geometrycznych.
• Grafika komputerowa i animacja: Tworzenie trójwymiarowych modeli, renderowanie obrazów, animowanie postaci wymaga znajomości geometrii przestrzennej i transformacji geometrycznych.
• Fizyka: Opisywanie ruchu ciał w przestrzeni, obliczanie sił i momentów wymaga znajomości wektorów i geometrii przestrzennej.

Więc, choć na pierwszy rzut oka może się wydawać, że obliczanie kąta między przekątną graniastosłupa a ścianą boczną to czysta teoria, to tak naprawdę jest to umiejętność, która może się przydać w wielu praktycznych zastosowaniach.

H2: Podsumowanie

Podsumowując, aby znaleźć kąt między przekątną graniastosłupa a ścianą boczną:

1. Zdefiniuj graniastosłup, ścianę boczną i przekątną.
2. Znajdź rzut przekątnej na ścianę boczną.
3. Zidentyfikuj trójkąt prostokątny utworzony przez przekątną, jej rzut i odcinek łączący ich końce.
4. Użyj funkcji trygonometrycznych (sinus, cosinus, tangens) aby obliczyć kąt.

Pamiętaj, że kluczem do sukcesu jest dobra wizualizacja i znajomość podstawowych pojęć z geometrii i trygonometrii. Powodzenia!