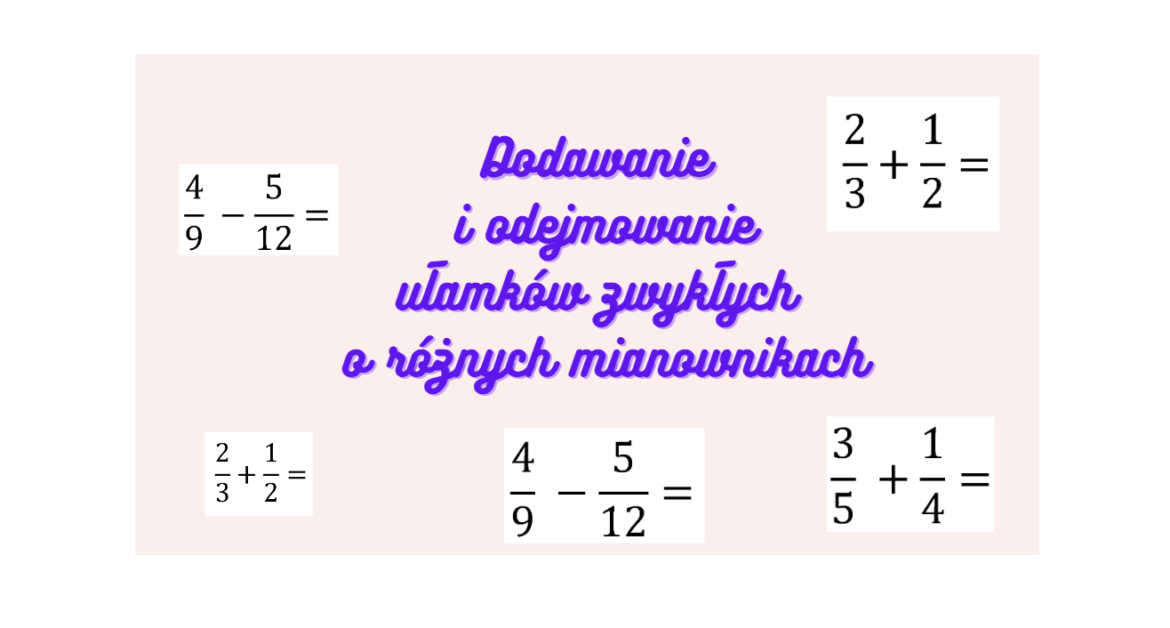
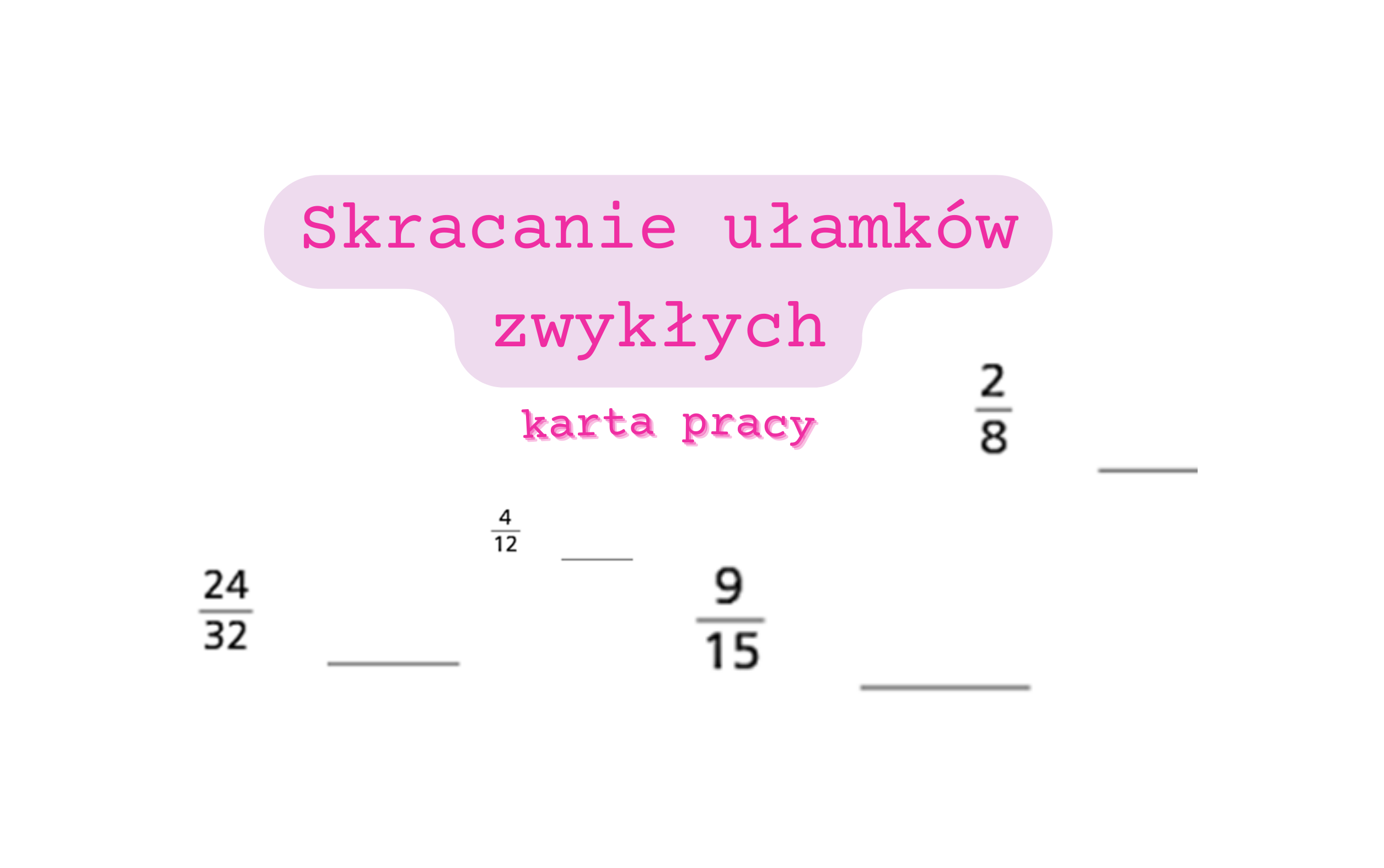
Karta Pracy Ułamki Zwykłe Klasa 5

W klasie 5 szkoły podstawowej uczniowie po raz pierwszy spotykają się z ułamkami zwykłymi na poważnie. Jest to moment przełomowy w ich edukacji matematycznej, ponieważ operacje na ułamkach są fundamentem do dalszej nauki, w tym algebry i geometrii. Zrozumienie ułamków zwykłych i umiejętność wykonywania na nich operacji jest kluczowe dla sukcesu w przyszłych przedmiotach ścisłych. Jednym z najskuteczniejszych narzędzi wspomagających naukę są karty pracy. Niniejszy artykuł przybliża, dlaczego karty pracy dotyczące ułamków zwykłych są tak ważne dla uczniów klasy 5 i jak efektywnie je wykorzystywać.

Dlaczego Ułamki Zwykłe Są Ważne?

Ułamki zwykłe to sposób reprezentowania części całości. To fundamentalne pojęcie matematyczne, które wykorzystywane jest w życiu codziennym o wiele częściej, niż zdajemy sobie sprawę. Od dzielenia pizzy po mierzenie składników w przepisie kulinarnym – ułamki są wszędzie.

Ułamki w Życiu Codziennym

Wyobraźmy sobie sytuację, gdy chcemy podzielić pizzę na 8 kawałków i zjeść 3 z nich. Możemy powiedzieć, że zjedliśmy 3/8 pizzy. Podobnie, jeśli potrzebujemy 1/2 szklanki mąki do ciasta, korzystamy z ułamka. Nawet podczas planowania czasu, gdy mówimy o kwadransie (1/4 godziny) lub pół godziny (1/2 godziny), używamy ułamków. Świadomość tych zastosowań pomaga uczniom zrozumieć, że ułamki nie są tylko abstrakcyjnym pojęciem matematycznym, ale realnym narzędziem.

Fundament Dalszej Edukacji

Ułamki zwykłe są podstawą do nauki ułamków dziesiętnych, procentów, proporcji i wielu innych zagadnień matematycznych. Bez solidnego zrozumienia ułamków zwykłych, uczniowie mogą mieć problemy z późniejszymi, bardziej zaawansowanymi tematami. Na przykład, algebra często opiera się na manipulacji wyrażeniami, które zawierają ułamki. Jeśli uczeń nie radzi sobie z dodawaniem czy odejmowaniem ułamków, zrozumienie równań algebraicznych będzie znacznie trudniejsze.

Zalety Kart Pracy z Ułamków Zwykłych

Karty pracy są cennym narzędziem dla nauczycieli i uczniów. Umożliwiają systematyczne ćwiczenie różnych umiejętności związanych z ułamkami zwykłymi i pozwalają na identyfikację obszarów, które wymagają dodatkowej pracy.

Ustrukturyzowana Praktyka

Karty pracy zwykle oferują uporządkowany zestaw zadań, który stopniowo wprowadza nowe koncepcje i utrwala już poznane. Zaczynają się od prostych ćwiczeń, takich jak rozpoznawanie ułamków na rysunkach, a następnie przechodzą do bardziej skomplikowanych operacji, takich jak dodawanie, odejmowanie, mnożenie i dzielenie ułamków. Dzięki temu uczniowie mogą systematycznie rozwijać swoje umiejętności.

Indywidualizacja Nauki

Karty pracy pozwalają na dostosowanie poziomu trudności do indywidualnych potrzeb ucznia. Nauczyciel może wybrać karty pracy, które odpowiadają poziomowi zaawansowania ucznia, co pozwala na efektywną naukę i unikanie frustracji. Uczniowie, którzy mają trudności z ułamkami, mogą pracować na prostszych kartach, podczas gdy ci bardziej zaawansowani mogą zmierzyć się z bardziej wymagającymi zadaniami. Możliwość indywidualizacji jest kluczowa dla zapewnienia, że każdy uczeń ma szansę na sukces.

Szybka Ocena Postępów

Nauczyciel może łatwo ocenić postępy uczniów, sprawdzając wykonane karty pracy. Pozwala to na szybkie zidentyfikowanie obszarów, w których uczniowie potrzebują dodatkowej pomocy. Jeśli wielu uczniów popełnia błędy w dodawaniu ułamków o różnych mianownikach, nauczyciel może poświęcić więcej czasu na omówienie tego tematu na lekcji. Informacje zwrotne uzyskane z kart pracy są niezwykle cenne dla planowania dalszych działań dydaktycznych.

Rodzaje Zadań na Kartach Pracy z Ułamków Zwykłych

Karty pracy powinny obejmować różnorodne typy zadań, aby kompleksowo rozwijać umiejętności uczniów.

Rozpoznawanie i Zapis Ułamków

Zadania te polegają na rozpoznawaniu i zapisywaniu ułamków przedstawionych na rysunkach (np. podzielonych figur geometrycznych) lub w formie opisowej. Uczniowie muszą zrozumieć, co reprezentuje licznik i mianownik ułamka. Przykładowo, zadaniem może być pokolorowanie 3/4 koła lub zapisanie, jaką część prostokąta zacieniono.

Porównywanie Ułamków

Uczniowie uczą się porównywać ułamki o tych samych mianownikach, różnych mianownikach oraz porównywać ułamki do 1/2 i 1. Wykorzystuje się znaki większości, mniejszości i równości. Przykładowo, zadaniem może być wstawienie odpowiedniego znaku pomiędzy 2/5 i 3/5 lub 1/3 i 1/2.

Rozszerzanie i Skracanie Ułamków

Te zadania koncentrują się na rozszerzaniu (mnożeniu licznika i mianownika przez tę samą liczbę) i skracaniu (dzieleniu licznika i mianownika przez tę samą liczbę) ułamków. Uczniowie uczą się, że rozszerzanie i skracanie nie zmienia wartości ułamka. Przykładowo, zadaniem może być rozszerzenie ułamka 1/2 do ułamka o mianowniku 6 lub skrócenie ułamka 4/8 do postaci nieskracalnej.

Dodawanie i Odejmowanie Ułamków

Uczniowie ćwiczą dodawanie i odejmowanie ułamków o tych samych mianownikach oraz o różnych mianownikach (wymagające sprowadzenia do wspólnego mianownika). Pamiętać trzeba o zapisywaniu wyniku w postaci nieskracalnej. Przykładowo, zadaniem może być obliczenie sumy 1/4 + 2/4 lub różnicy 3/5 - 1/10.

Mnożenie i Dzielenie Ułamków

Te zadania wprowadzają mnożenie i dzielenie ułamków zwykłych. Uczniowie uczą się mnożyć ułamek przez ułamek oraz dzielić ułamek przez ułamek (mnożenie przez odwrotność). Przykładowo, zadaniem może być obliczenie iloczynu 1/2 * 2/3 lub ilorazu 3/4 : 1/2.

Zadania Tekstowe

Zadania tekstowe pozwalają uczniom na zastosowanie wiedzy o ułamkach w praktycznych sytuacjach. Wymagają analizy treści zadania, identyfikacji kluczowych informacji i wykonania odpowiednich operacji na ułamkach. Przykładowo: „Ania zjadła 1/3 ciasta, a Kasia 1/4 ciasta. Jaką część ciasta zjadły razem?”.

Przykłady Danych i Zastosowań

Z badań wynika, że uczniowie, którzy regularnie ćwiczą operacje na ułamkach zwykłych, osiągają lepsze wyniki w dalszej edukacji matematycznej. Na przykład, analiza wyników testów z matematyki na koniec szkoły podstawowej często wykazuje silną korelację między umiejętnością operowania ułamkami a ogólnym wynikiem. Ponadto, umiejętność pracy z ułamkami jest niezbędna w wielu zawodach, takich jak inżynier, architekt, kucharz czy finansista.

Według danych zebranych przez Centralną Komisję Egzaminacyjną, zadania z ułamków zwykłych regularnie pojawiają się na egzaminach zewnętrznych. Oznacza to, że solidne opanowanie tego tematu jest kluczowe dla osiągnięcia sukcesu na egzaminach i kontynuacji edukacji.

Wskazówki dla Nauczycieli

Nauczyciele powinni aktywnie wykorzystywać karty pracy w procesie nauczania ułamków zwykłych.

Wybierać karty pracy o różnym stopniu trudności, aby zaspokoić potrzeby wszystkich uczniów.
Dostarczać uczniom jasne instrukcje i wyjaśnienia.
Zachęcać uczniów do samodzielnego rozwiązywania zadań, ale oferować pomoc w razie potrzeby.
Wykorzystywać karty pracy do diagnozowania trudności uczniów i planowania dalszych działań.
Stosować różnorodne formy pracy z kartami – indywidualną, w parach, w grupach.

Wskazówki dla Uczniów

Uczniowie powinni wykorzystywać karty pracy jako narzędzie do samodzielnej nauki i utrwalania wiedzy.

Uważnie czytać polecenia i starać się zrozumieć, o co są pytani.
Samodzielnie rozwiązywać zadania, a w razie trudności prosić o pomoc nauczyciela lub kolegę.
Sprawdzać swoje odpowiedzi i analizować popełnione błędy.
Regularnie ćwiczyć operacje na ułamkach, aby utrwalać wiedzę.
Traktować karty pracy jako okazję do samodzielnego odkrywania matematyki.

Podsumowanie i Wezwanie do Działania

Karty pracy z ułamków zwykłych to nieocenione narzędzie w edukacji matematycznej uczniów klasy 5. Pozwalają na systematyczne ćwiczenie, indywidualizację nauki i szybką ocenę postępów. Zarówno nauczyciele, jak i uczniowie powinni aktywnie korzystać z kart pracy, aby skutecznie opanować wiedzę o ułamkach zwykłych i przygotować się do dalszej nauki matematyki. Zacznij już dziś! Poszukaj darmowych kart pracy online, zapytaj nauczyciela o dodatkowe materiały lub stwórz własne karty pracy z przykładami, które sprawiają Ci najwięcej trudności. Pamiętaj, praktyka czyni mistrza!