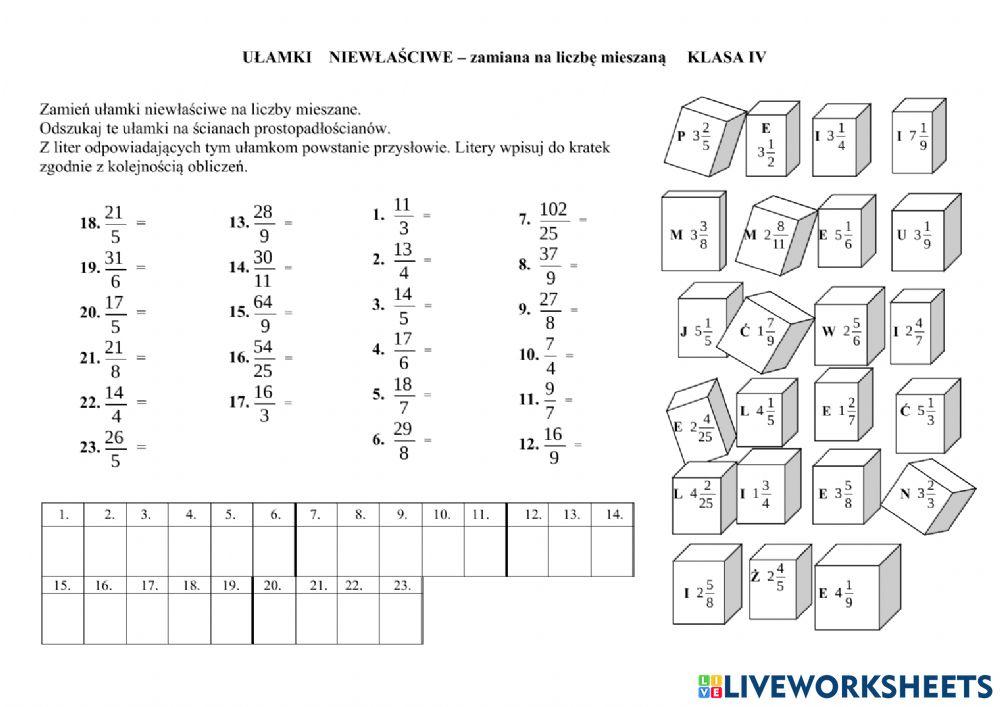
Karta Pracy Ułamki Zwykłe Klasa 4

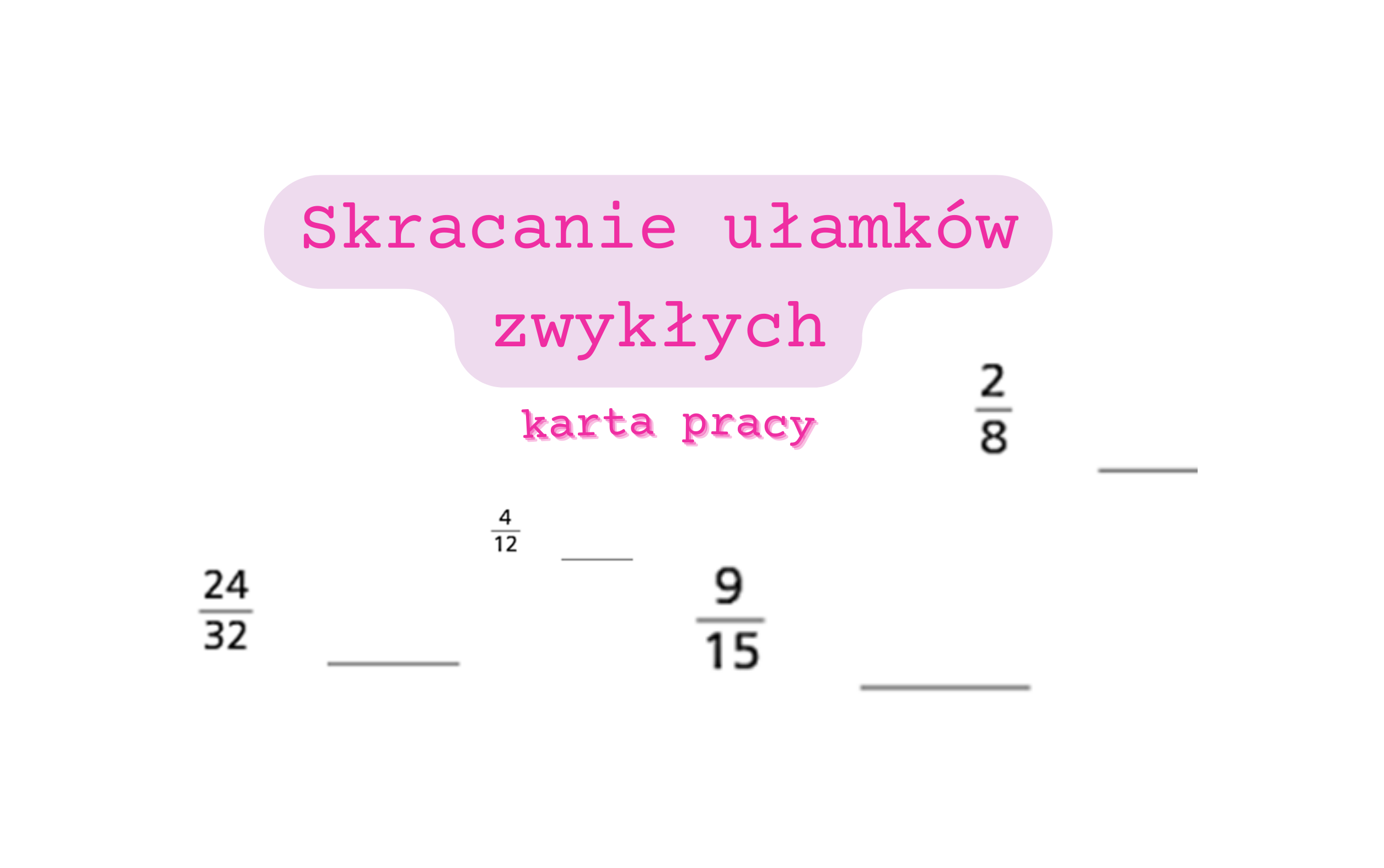
Ułamki zwykłe to podstawa matematyki, a zrozumienie ich już w 4 klasie szkoły podstawowej ma ogromny wpływ na dalszą edukację. Karta pracy z ułamkami zwykłymi dla klasy 4 powinna być skonstruowana tak, aby wprowadzić dzieci w świat ułamków w sposób przystępny, angażujący i skuteczny. Celem jest, aby uczniowie nie tylko zapamiętali definicje, ale przede wszystkim zrozumieli, co ułamek tak naprawdę oznacza i jak można go używać w życiu codziennym.

Czym są ułamki zwykłe? Wprowadzenie do tematu.

Ułamek zwykły to sposób na przedstawienie części całości. Składa się z dwóch liczb, zapisanych jedna nad drugą, oddzielonych poziomą kreską. Liczba na górze to licznik, a liczba na dole to mianownik. Mianownik informuje nas, na ile równych części podzieliliśmy całość, a licznik mówi, ile tych części bierzemy pod uwagę.

Na przykład, ułamek 1/2 (czytamy "jedna druga") oznacza, że całość została podzielona na dwie równe części i bierzemy jedną z nich. Ułamek 3/4 (czytamy "trzy czwarte") oznacza, że całość została podzielona na cztery równe części i bierzemy trzy z nich.

Zastosowanie w praktyce

Ważne jest, aby od razu pokazywać dzieciom, gdzie mogą spotkać ułamki zwykłe w życiu codziennym. Oto kilka przykładów:

Krojenie pizzy: Jeśli pizza jest pokrojona na 8 kawałków, a zjesz 3 kawałki, to zjadłeś 3/8 pizzy.
Dzielenie czekolady: Jeśli czekolada ma 10 kostek, a dasz koledze 2 kostki, to dałeś mu 2/10 czekolady.
Odmierzanie składników w przepisie: Często przepisy wymagają użycia np. 1/2 szklanki mąki.

Karta Pracy – Co powinna zawierać?

Dobra karta pracy z ułamkami zwykłymi dla klasy 4 powinna zawierać różnorodne zadania, które stopniowo wprowadzają i utrwalają wiedzę. Powinna angażować różne style uczenia się (wizualny, słuchowy, kinestetyczny) i dostosowywać się do indywidualnego tempa pracy każdego ucznia.

Identyfikacja ułamków

Pierwszym krokiem jest nauczenie dzieci rozpoznawania ułamków. Zadania mogą polegać na:

Rysowaniu: Uczniowie rysują koło, kwadrat lub prostokąt i dzielą go na odpowiednią liczbę części, a następnie kolorują określoną liczbę części, aby przedstawić dany ułamek.
Wybieraniu prawidłowego ułamka: Nauczyciel pokazuje obrazek (np. pokrojoną pizzę) i uczniowie wybierają spośród kilku opcji prawidłowy ułamek, który opisuje, jaka część pizzy została zjedzona.
Wpisywaniu licznika i mianownika: Na obrazku jest pokazana np. podzielona tabliczka czekolady, a uczniowie muszą wpisać odpowiedni licznik i mianownik.

Porównywanie ułamków

Kolejny ważny krok to nauczenie dzieci porównywania ułamków, czyli stwierdzania, który ułamek jest większy, a który mniejszy. Na początku warto skupić się na ułamkach o tych samych mianownikach.

Ułamki o tym samym mianowniku: Tutaj sprawa jest prosta – im większy licznik, tym większy ułamek. Na przykład, 3/5 jest większe niż 1/5. Zadania mogą polegać na porównywaniu par ułamków i wstawianiu znaków >, < lub =.
Ułamki o tym samym liczniku: Tutaj sytuacja jest odwrotna – im większy mianownik, tym mniejszy ułamek. Na przykład, 1/4 jest większe niż 1/8. Podobnie jak wcześniej, uczniowie porównują pary ułamków i wstawiają odpowiednie znaki.
Ułamki o różnych licznikach i mianownikach: To jest bardziej zaawansowany etap, który można wprowadzić później. Wymaga sprowadzania ułamków do wspólnego mianownika lub korzystania z innych metod porównywania.

Dodawanie i odejmowanie ułamków o tych samych mianownikach

Następnym etapem jest wprowadzenie dodawania i odejmowania ułamków, ale na początku tylko tych o tych samych mianownikach. Jest to stosunkowo proste – dodajemy lub odejmujemy tylko liczniki, a mianownik pozostaje bez zmian.

Dodawanie: Na przykład, 2/7 + 3/7 = 5/7. Zadania mogą polegać na rozwiązywaniu prostych przykładów dodawania ułamków.
Odejmowanie: Na przykład, 5/8 - 2/8 = 3/8. Podobnie jak wcześniej, uczniowie rozwiązują proste przykłady odejmowania ułamków.
Zadania tekstowe: Ważne jest, aby pokazywać dzieciom, jak dodawanie i odejmowanie ułamków może być użyteczne w życiu codziennym. Na przykład: "Ania zjadła 1/4 ciasta, a Kasia zjadła 2/4 ciasta. Ile ciasta zjadły razem?".

Ułamki jako części zbioru

Ułamki można również rozumieć jako części zbioru, a nie tylko części całości. Na przykład, jeśli mamy 10 cukierków, a 3 z nich są czerwone, to czerwone cukierki stanowią 3/10 wszystkich cukierków.

Zadania z cukierkami, klockami, piłkami: Nauczyciel pokazuje zbiór przedmiotów (np. 12 klocków) i pyta, jaka część klocków jest niebieska. Uczniowie muszą policzyć niebieskie klocki i zapisać odpowiedni ułamek.
Obrazki: Na kartach pracy mogą być obrazki przedstawiające zbiory przedmiotów, a uczniowie muszą określić, jaka część zbioru spełnia określony warunek (np. jaka część jabłek jest czerwona).

Metody nauczania ułamków zwykłych

Skuteczna nauka ułamków zwykłych wymaga stosowania różnorodnych metod i technik. Oto kilka sprawdzonych sposobów:

Wykorzystanie materiałów manipulacyjnych

Materiały manipulacyjne, takie jak klocki, patyczki, koła podzielone na części, są niezastąpione w nauce ułamków. Dzieci mogą fizycznie dzielić, łączyć i porównywać ułamki, co pomaga im zrozumieć abstrakcyjne pojęcia.

Gry i zabawy

Gry i zabawy to świetny sposób na utrwalenie wiedzy w sposób atrakcyjny i angażujący. Można wykorzystać np. karty z ułamkami do gry w memo, domino lub loteryjkę. Można również tworzyć proste gry planszowe, w których uczniowie przesuwają się po planszy, rozwiązując zadania z ułamkami.

Praca w grupach

Praca w grupach sprzyja współpracy, wymianie wiedzy i uczeniu się od siebie nawzajem. Uczniowie mogą wspólnie rozwiązywać zadania, tłumaczyć sobie nawzajem trudne zagadnienia i dzielić się swoimi pomysłami.

Wykorzystanie technologii

Warto wykorzystać dostępne narzędzia online, takie jak interaktywne ćwiczenia, gry edukacyjne i filmy animowane. Technologia może uatrakcyjnić naukę i dostosować ją do indywidualnych potrzeb każdego ucznia.

Przykładowe zadania na karcie pracy

Oto kilka przykładowych zadań, które mogą znaleźć się na karcie pracy z ułamkami zwykłymi dla klasy 4:

Pokoloruj 1/3 koła na niebiesko.
Wpisz licznik i mianownik ułamka, który przedstawia zamalowaną część figury.
Porównaj ułamki: 2/5 i 4/5 (wstaw znak >, < lub =).
Oblicz: 1/4 + 2/4 =
W klasie jest 20 uczniów. 1/2 uczniów lubi matematykę. Ile uczniów lubi matematykę?

Błędy, których należy unikać

Podczas nauki ułamków zwykłych, ważne jest, aby unikać pewnych błędów, które mogą utrudnić dzieciom zrozumienie tematu:

Przedwczesne wprowadzanie skomplikowanych zagadnień: Nie należy zaczynać od dodawania ułamków o różnych mianownikach, zanim uczniowie dobrze opanują podstawowe pojęcia i umiejętności.
Brak powiązania z życiem codziennym: Ważne jest, aby pokazywać dzieciom, gdzie mogą spotkać ułamki w rzeczywistości, aby miały motywację do nauki.
Stosowanie tylko jednego stylu nauczania: Należy uwzględniać różne style uczenia się i stosować różnorodne metody i techniki.
Brak indywidualnego podejścia: Należy dostosowywać tempo nauki i poziom trudności zadań do indywidualnych potrzeb każdego ucznia.

Podsumowanie

Nauka ułamków zwykłych w 4 klasie szkoły podstawowej jest kluczowa dla dalszego rozwoju matematycznego ucznia. Dzięki odpowiednio skonstruowanej karcie pracy, wykorzystaniu różnorodnych metod nauczania i uwzględnieniu indywidualnych potrzeb każdego dziecka, możemy sprawić, że ułamki staną się dla nich zrozumiałe i ciekawe. Pamiętajmy o praktycznych przykładach, angażujących zadaniach i wspierającej atmosferze, która zachęci uczniów do odkrywania świata ułamków!

Zachęcamy do eksperymentowania z różnymi formami kart pracy i metodami nauczania, aby znaleźć te, które najlepiej sprawdzają się w przypadku konkretnej grupy uczniów. Pamiętajmy, że cierpliwość i pozytywne nastawienie są kluczem do sukcesu w nauce matematyki!