Jakie Pole Ma Trójkąt Abc A 54

Zastanawiasz się, jak obliczyć pole trójkąta ABC, wiedząc że A wynosi 54? To pytanie, które spędza sen z powiek wielu uczniom, a czasami nawet i dorosłym, którzy nagle muszą odświeżyć wiedzę z geometrii. Nie martw się! Nie jesteś sam. Geometria może wydawać się zawiła, ale obiecuję, że postaram się wytłumaczyć to w sposób jak najbardziej przystępny. Problem często tkwi w niepełnej informacji. Wiedząc tylko, że 'A' (co rozumiem jako pole trójkąta) wynosi 54, nie jesteśmy w stanie jednoznacznie określić wymiarów trójkąta, ani jego kształtu. Spróbujmy jednak to rozłożyć na czynniki pierwsze.

Co tak naprawdę wiemy?

W tym momencie wiemy jedno: Pole trójkąta ABC wynosi 54 jednostki kwadratowe. Oznacza to, że przestrzeń wewnątrz tego trójkąta zajmuje obszar o wielkości 54. Ale to wszystko! Nie wiemy, czy to trójkąt równoboczny, równoramienny, prostokątny, czy też zupełnie "dziki" trójkąt różnoboczny. To tak jakbyśmy mieli tylko informację o kubaturze pudełka, ale nie wiedzieli, jakie są jego wymiary.

Wzory na pole trójkąta

Żeby zacząć jakiekolwiek obliczenia, musimy przypomnieć sobie wzory na pole trójkąta. Najczęściej używane to:

Podstawa razy wysokość podzielone przez 2: P = (a * h) / 2 (gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę)
Wzór Herona: P = √(s(s-a)(s-b)(s-c)) (gdzie 'a', 'b', 'c' to długości boków trójkąta, a 's' to połowa obwodu: s = (a+b+c)/2)
Używając sinusa kąta: P = (1/2) * a * b * sin(γ) (gdzie 'a' i 'b' to długości dwóch boków, a γ to kąt między nimi)

Każdy z tych wzorów wymaga od nas posiadania dodatkowych informacji. Bez nich, bazując tylko na wartości pola, nie jesteśmy w stanie obliczyć konkretnych wymiarów trójkąta.

Potrzebne dodatkowe informacje

Skoro mamy tylko pole, musimy założyć, że mamy szansę na obliczenie wymiarów trójkąta, jeśli otrzymamy dodatkowe dane. Może to być:

Długość jednego boku i odpowiadająca mu wysokość.
Długości dwóch boków i miara kąta między nimi.
Długości wszystkich trzech boków.
Informacja, że trójkąt jest specyficznego typu (np. równoboczny, prostokątny równoramienny).

Bez jednej z tych informacji, zadanie jest nierozwiązywalne w sposób jednoznaczny.

Przykładowe scenariusze

Rozważmy kilka hipotetycznych sytuacji:

Scenariusz 1: Wiemy, że podstawa trójkąta ma długość 12. Wtedy możemy obliczyć wysokość: 54 = (12 * h) / 2 => h = (54 * 2) / 12 = 9. Czyli wysokość trójkąta wynosi 9.
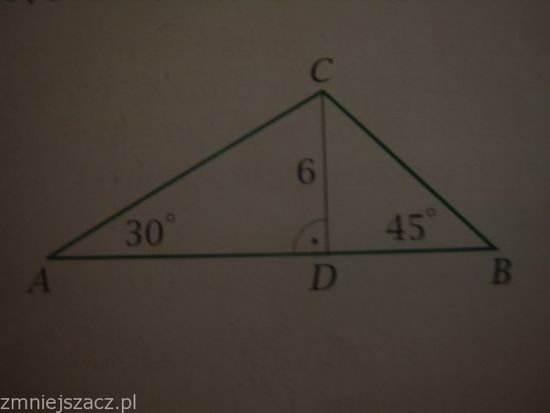
Scenariusz 2: Wiemy, że trójkąt jest prostokątny, a jedna z przyprostokątnych ma długość 6. W takim przypadku pole trójkąta prostokątnego liczymy jako połowę iloczynu przyprostokątnych. Zatem 54 = (6 * b) / 2 => b = (54 * 2) / 6 = 18. Druga przyprostokątna ma długość 18.
Scenariusz 3: Załóżmy, że mamy trójkąt równoboczny. Wtedy pole trójkąta równobocznego możemy obliczyć ze wzoru: P = (a²√3) / 4. Wtedy 54 = (a²√3) / 4 => a² = (54*4)/√3 => a = √(216/√3) ≈ 11.17. Długość boku trójkąta równobocznego wynosi około 11.17.

Widzisz? Za każdym razem, kiedy dodajemy informację, jesteśmy w stanie coś obliczyć!

A co jeśli ktoś powie, że to zadanie ma za mało danych?

Możesz spotkać się z opinią, że bez dodatkowych danych zadanie jest niemożliwe do rozwiązania. I to jest prawda, jeśli szukamy konkretnych, jednoznacznych wymiarów trójkąta. Matematyka jest precyzyjna. Ale...

... możemy też potraktować to jako zadanie otwarte. Możemy powiedzieć, że istnieje nieskończenie wiele trójkątów o polu 54. Możemy tworzyć pary (podstawa, wysokość) spełniające równanie (a * h) / 2 = 54. Na przykład:

a = 1, h = 108
a = 2, h = 54
a = 3, h = 36
a = 4, h = 27
a = 6, h = 18
a = 9, h = 12
a = 12, h = 9
a = 18, h = 6
a = 27, h = 4
a = 36, h = 3
a = 54, h = 2
a = 108, h = 1

To tylko kilka przykładów! Możemy tworzyć takie pary w nieskończoność, co pokazuje, że istnieje nieskończenie wiele trójkątów o polu 54.

Przeciwności i ograniczenia

Krytycy mogliby argumentować, że takie "rozwiązanie" jest bezużyteczne, bo nie prowadzi do konkretnego trójkąta. I to jest częściowo prawda. Nie otrzymujemy konkretnych wymiarów. Ale...

... zrozumienie, że istnieje wiele możliwości, jest bardzo ważne. Uczy nas to myślenia abstrakcyjnego i elastycznego podejścia do problemów. Pokazuje, że jedno pytanie może mieć wiele odpowiedzi, w zależności od tego, jak je zinterpretujemy.

Podsumowanie i rozwiązanie (w pewnym sensie)

Podsumowując, nie możemy jednoznacznie określić wymiarów trójkąta ABC, wiedząc tylko, że jego pole wynosi 54. Potrzebujemy dodatkowych danych, takich jak długość boku i wysokość, długości dwóch boków i kąt między nimi, długości wszystkich trzech boków, lub informacja o rodzaju trójkąta.

Jednakże, możemy potraktować to jako zadanie otwarte i stwierdzić, że istnieje nieskończenie wiele trójkątów o polu 54. Możemy tworzyć pary (podstawa, wysokość) spełniające równanie (a * h) / 2 = 54.

Co dalej?

Mam nadzieję, że to wyjaśnienie pomogło Ci zrozumieć problem obliczania pola trójkąta i potrzebę posiadania odpowiednich danych. Jeśli masz dodatkowe informacje o trójkącie ABC (np. długość boku, rodzaj trójkąta), spróbuj użyć odpowiedniego wzoru, aby obliczyć jego wymiary.

A jeśli nie masz dodatkowych danych, możesz potraktować to jako wyzwanie kreatywne: spróbuj narysować kilka różnych trójkątów, które Twoim zdaniem mogłyby mieć pole równe 54! To świetny sposób na utrwalenie wiedzy i rozwijanie wyobraźni geometrycznej.

Czy to zadanie sprawiło, że spojrzałeś na geometrię z nowej perspektywy? A może masz jeszcze jakieś pytania dotyczące obliczania pola trójkątów?