Jakie Liczby X Spełniają Równanie

Zastanawiałeś się kiedyś, które liczby "pasują" do danego równania? To pytanie, które łączy matematykę z codziennym życiem, choć na pierwszy rzut oka może się to nie wydawać. Rozwiązanie równania to nic innego jak znalezienie wartości, które, po podstawieniu w miejsce niewiadomej (najczęściej oznaczanej jako "x"), sprawią, że lewa strona równania będzie równa prawej. Brzmi prosto, prawda? Ale diabeł tkwi w szczegółach, a te bywają zaskakująco złożone.

Dlaczego Znajdowanie Rozwiązań Równań Jest Ważne?

Może wydawać się, że rozwiązywanie równań to domena matematyków i naukowców w laboratoriach. Nic bardziej mylnego! Równania są wszędzie, kształtują nasz świat bardziej, niż sobie wyobrażamy.

• Inżynieria: Projektując mosty, budynki czy nawet smartfony, inżynierowie muszą rozwiązywać równania opisujące wytrzymałość materiałów, obciążenia i przepływ prądu.
• Finanse: Obliczanie rat kredytów, stóp procentowych, zysków z inwestycji – wszystko to opiera się na równaniach.
• Medycyna: Dawkowanie leków, modelowanie rozprzestrzeniania się chorób, analiza wyników badań – równania są niezbędne w diagnostyce i leczeniu.
• Prognozowanie Pogody: Modele meteorologiczne wykorzystują skomplikowane równania, aby przewidywać zmiany temperatur, opady i inne zjawiska atmosferyczne.

Brak umiejętności rozwiązywania równań ogranicza naszą zdolność do rozumienia świata i podejmowania świadomych decyzji. Wyobraź sobie, że chcesz wziąć kredyt – bez znajomości podstaw matematyki łatwo możesz zostać oszukany przez nieuczciwego pożyczkodawcę.

Jakie Liczby "Pasują"? Różne Typy Równań i Ich Rozwiązania

W zależności od rodzaju równania, zbiór liczb, które spełniają to równanie, może być różny. Przyjrzyjmy się kilku przykładom:

Równania Liniowe

To najprostszy rodzaj równań. Mają postać ax + b = 0, gdzie a i b to stałe, a x to niewiadoma. Rozwiązanie to po prostu x = -b/a.

Przykład: 2x + 4 = 0. Rozwiązaniem jest x = -2. Tylko jedna liczba spełnia to równanie.

Równania Kwadratowe

Mają postać ax² + bx + c = 0, gdzie a, b i c to stałe, a a ≠ 0. Rozwiązaniem są pierwiastki równania, które można znaleźć za pomocą wzoru na deltę (Δ = b² - 4ac) i pierwiastków: x₁ = (-b - √Δ) / 2a i x₂ = (-b + √Δ) / 2a.

• Δ > 0: Dwa różne rozwiązania rzeczywiste.
• Δ = 0: Jedno rozwiązanie rzeczywiste (pierwiastek podwójny).
• Δ < 0: Brak rozwiązań rzeczywistych (są dwa rozwiązania zespolone).

Przykład: x² - 5x + 6 = 0. Δ = 1, x₁ = 2, x₂ = 3. Dwie liczby spełniają to równanie.

Równania Wielomianowe Wyższego Stopnia

Równania postaci aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀ = 0. Znalezienie rozwiązań takich równań może być bardzo trudne, a czasami niemożliwe analitycznie (tzn. za pomocą wzorów). Często stosuje się metody numeryczne, aby znaleźć przybliżone rozwiązania.

Przykład: x³ - 6x² + 11x - 6 = 0. Można zauważyć, że x=1 jest rozwiązaniem. Dzieląc wielomian przez (x-1), otrzymujemy równanie kwadratowe, które możemy rozwiązać. Rozwiązania to x=1, x=2, x=3.

Równania Trygonometryczne

Równania zawierające funkcje trygonometryczne (sinus, cosinus, tangens, cotangens). Rozwiązania takich równań zazwyczaj powtarzają się co pewien okres.

Przykład: sin(x) = 0. Rozwiązania to x = kπ, gdzie k jest liczbą całkowitą (..., -2π, -π, 0, π, 2π, ...). Nieskończenie wiele liczb spełnia to równanie.

Równania Wykładnicze i Logarytmiczne

Równania, w których niewiadoma występuje w wykładniku potęgi lub w argumencie logarytmu. Rozwiązanie wymaga zastosowania właściwości potęg i logarytmów.

Przykład: 2ˣ = 8. Rozwiązaniem jest x = 3. Tylko jedna liczba spełnia to równanie.

"X" Może Być Czymkolwiek! Zbiory Liczbowe i Dziedziny Równań

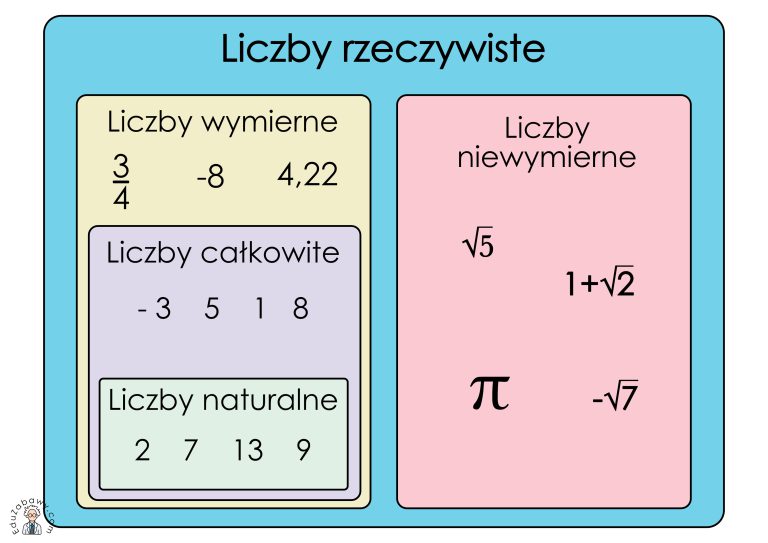
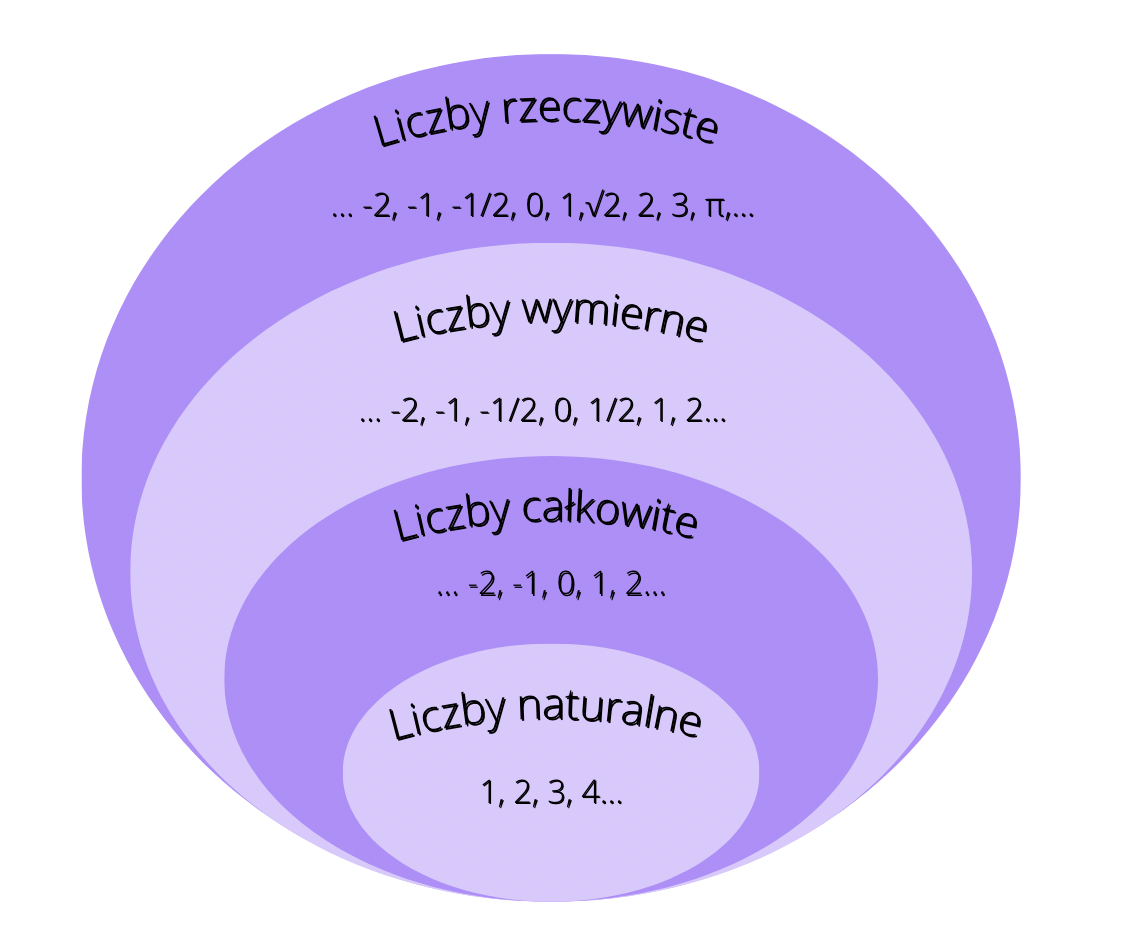
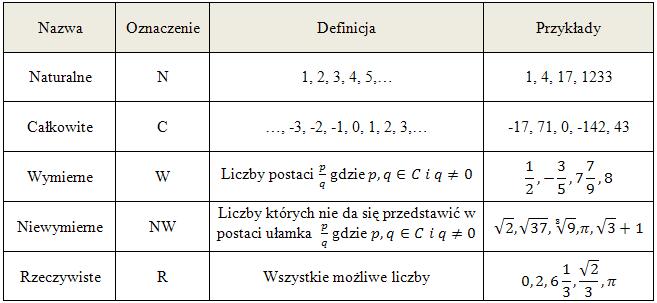
Bardzo ważne jest zrozumienie, w jakim zbiorze szukamy rozwiązań. Często domyślnie rozważamy liczby rzeczywiste (oznaczane symbolem ℝ), ale rozwiązania mogą istnieć tylko w zbiorze liczb naturalnych (ℕ), całkowitych (ℤ) lub zespolonych (ℂ). Na przykład:

• Równanie x + 5 = 2 ma rozwiązanie x = -3, które należy do zbioru liczb całkowitych (ℤ), ale nie do zbioru liczb naturalnych (ℕ).
• Równanie x² = -1 nie ma rozwiązań w zbiorze liczb rzeczywistych (ℝ), ale ma rozwiązania w zbiorze liczb zespolonych (ℂ): x = i oraz x = -i (gdzie i to jednostka urojona, √-1).

Dodatkowo, niektóre równania mają ograniczenia dotyczące dziedziny. Na przykład, w równaniach logarytmicznych argument logarytmu musi być liczbą dodatnią. W równaniach z ułamkami, mianownik nie może być równy zero. Musimy pamiętać o tych ograniczeniach, aby uniknąć błędnych rozwiązań.

Przeciwnicy Znajomości Rozwiązywania Równań?

Można spotkać się z opinią, że w dobie komputerów i kalkulatorów, umiejętność ręcznego rozwiązywania równań jest zbędna. Przecież programy potrafią to zrobić szybciej i dokładniej! Jest w tym trochę prawdy, ale umiejętność rozwiązywania równań rozwija logiczne myślenie, uczy analizy problemów i pozwala zrozumieć zasady, na których działają algorytmy. Rozumienie procesu jest ważniejsze niż samo uzyskanie wyniku. Bez tej wiedzy jesteśmy tylko "użytkownikami" narzędzi, a nie twórcami i innowatorami.

Kolejnym argumentem jest to, że "matematyka jest zbyt abstrakcyjna i nieprzydatna w życiu codziennym". Jak już wspomnieliśmy na początku, równania są obecne w wielu dziedzinach i pomagają nam podejmować lepsze decyzje. Nawet proste równanie pozwalające obliczyć, ile kosztuje zakupy z uwzględnieniem rabatu, jest przykładem praktycznego zastosowania matematyki.

Klucz do Sukcesu: Metody Rozwiązywania Równań

Nie ma jednej uniwersalnej metody na rozwiązywanie wszystkich równań. Wiele zależy od rodzaju równania i naszych umiejętności. Oto kilka przydatnych strategii:

• Uproszczenie: Dąż do uproszczenia równania poprzez redukcję wyrazów podobnych, rozwijanie nawiasów, stosowanie tożsamości algebraicznych i trygonometrycznych.
• Izolacja niewiadomej: Przekształcaj równanie tak, aby niewiadoma "x" znalazła się po jednej stronie równania, a wszystkie pozostałe wyrazy po drugiej stronie.
• Podstawienie: W bardziej skomplikowanych równaniach warto wprowadzić nową zmienną, aby uprościć problem.
• Metody numeryczne: Jeśli nie można znaleźć rozwiązania analitycznego, skorzystaj z metod numerycznych, takich jak metoda bisekcji, metoda Newtona-Raphsona lub solverów dostępnych w programach komputerowych.
• Sprawdzenie rozwiązania: Zawsze sprawdź, czy znalezione rozwiązanie spełnia równanie. Podstaw wyliczoną wartość "x" do równania i upewnij się, że lewa strona jest równa prawej.

Pamiętaj, że praktyka czyni mistrza. Im więcej równań rozwiążesz, tym lepiej zrozumiesz różne techniki i będziesz w stanie szybciej i skuteczniej radzić sobie z nowymi problemami.

Podsumowanie: Szukaj Dalej, Eksperymentuj i Nie Bój Się Błędów!

Znalezienie liczb, które spełniają dane równanie, to fascynująca podróż po świecie matematyki. To nie tylko mechaniczne stosowanie wzorów, ale przede wszystkim proces logicznego myślenia, analizy i kreatywnego rozwiązywania problemów. Równania otaczają nas wszędzie, więc umiejętność ich rozwiązywania jest niezwykle przydatna w życiu codziennym i zawodowym. Nie zrażaj się trudnościami, eksperymentuj, ucz się na błędach i ciesz się satysfakcją z każdego rozwiązanego równania!

Zatem, jakie równanie spróbujesz rozwiązać jako następne?