Jaki Jest Wzór Na Pole Trójkąta

Czy kiedykolwiek zastanawiałeś się, jak łatwo obliczyć powierzchnię trójkąta? Niezależnie od tego, czy jesteś uczniem przygotowującym się do egzaminu z matematyki, majsterkowiczem planującym remont dachu, czy po prostu ciekawą osobą, zrozumienie wzoru na pole trójkąta może być zaskakująco przydatne. Wielu z nas pamięta z lekcji matematyki tajemnicze formuły, ale często zapominamy, jak je praktycznie zastosować. Ten artykuł ma na celu uproszczenie tego procesu, wyjaśniając wzór na pole trójkąta w sposób jasny, zrozumiały i co najważniejsze - użyteczny.

Podstawowy Wzór na Pole Trójkąta

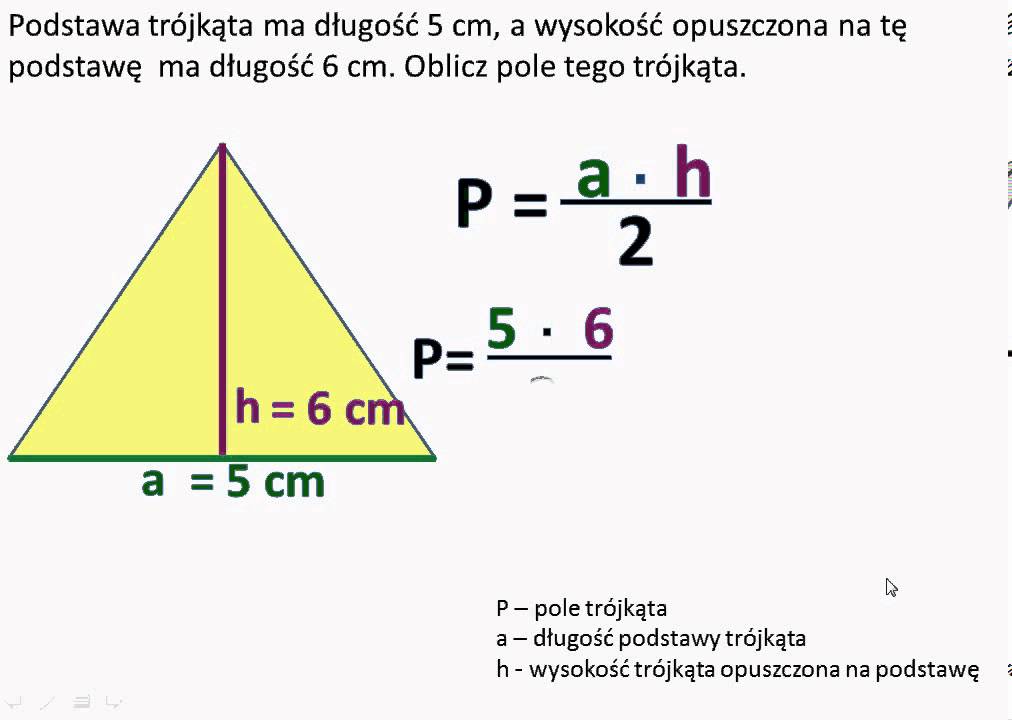
Najbardziej znanym i najczęściej stosowanym wzorem na pole trójkąta jest ten, który wykorzystuje długość jego podstawy (a) i wysokość (h) opuszczoną na tę podstawę. Wzór ten prezentuje się następująco:

Pole = ¹/₂ * a * h

Czyli: Pole trójkąta równa się połowie iloczynu długości jego podstawy i wysokości.

Wyjaśnienie: Podstawa (a) to dowolny bok trójkąta, a wysokość (h) to odcinek prostopadły do podstawy, łączący ją z przeciwległym wierzchołkiem. Wyobraź sobie, że masz trójkąt narysowany na kartce. Wybierz jeden z boków jako podstawę. Następnie, narysuj linię prostą, wychodzącą z wierzchołka naprzeciwko wybranej podstawy i padającą prostopadle (pod kątem 90 stopni) na tę podstawę. Długość tej prostej to właśnie wysokość.

Przykład: Załóżmy, że podstawa trójkąta ma długość 10 cm, a wysokość opuszczona na tę podstawę wynosi 6 cm. Wtedy pole trójkąta wynosi: Pole = ¹/₂ * 10 cm * 6 cm = 30 cm².

Wzór Herona: Kiedy Znamy Długości Wszystkich Boków

Co jednak zrobić, gdy nie znamy wysokości trójkąta, ale za to znamy długości wszystkich jego boków? W takiej sytuacji możemy skorzystać ze wzoru Herona. Ten wzór jest nieco bardziej skomplikowany, ale niezwykle przydatny. Wzór Herona wygląda następująco:

Pole = √[s(s-a)(s-b)(s-c)]

Gdzie:

• a, b, c to długości boków trójkąta,
• s to połowa obwodu trójkąta, czyli s = ^(a+b+c)/₂

Wyjaśnienie: Wzór Herona pozwala obliczyć pole trójkąta, znając jedynie długości jego boków. Najpierw obliczamy połowę obwodu (s), a następnie podstawiamy wartości do wzoru. Pamiętaj, żeby najpierw wykonać działania w nawiasach, a na końcu wyciągnąć pierwiastek kwadratowy.

Przykład: Załóżmy, że boki trójkąta mają długości: a = 5 cm, b = 7 cm, c = 8 cm. Wtedy:

1. Obliczamy połowę obwodu: s = ^(5+7+8)/₂ = 10 cm
2. Podstawiamy wartości do wzoru Herona: Pole = √[10(10-5)(10-7)(10-8)] = √[10 * 5 * 3 * 2] = √300 ≈ 17.32 cm²

Wzór z Wykorzystaniem Sinusa Kąta

Istnieje jeszcze jeden wzór na pole trójkąta, który wykorzystuje długości dwóch boków i sinus kąta między nimi. Ten wzór jest szczególnie przydatny, gdy znamy długości dwóch boków i miarę kąta zawartego między nimi.

Pole = ¹/₂ * a * b * sin(γ)

Gdzie:

• a i b to długości dwóch boków trójkąta,
• γ to kąt zawarty między bokami a i b,
• sin(γ) to sinus kąta γ.

Wyjaśnienie: Sinus kąta to funkcja trygonometryczna, której wartość można odczytać z tabeli wartości funkcji trygonometrycznych lub obliczyć za pomocą kalkulatora naukowego. Ważne jest, aby upewnić się, że kalkulator jest ustawiony na stopnie (degrees) lub radiany (radians) w zależności od tego, w jakiej jednostce podana jest miara kąta.

Przykład: Załóżmy, że boki trójkąta mają długości: a = 8 cm, b = 6 cm, a kąt między nimi wynosi 30 stopni. Wtedy:

1. Obliczamy sinus kąta: sin(30°) = 0.5
2. Podstawiamy wartości do wzoru: Pole = ¹/₂ * 8 cm * 6 cm * 0.5 = 12 cm²

Kiedy Który Wzór Wybrać?

Wybór odpowiedniego wzoru na pole trójkąta zależy od dostępnych danych.

• Jeśli znamy długość podstawy i wysokość opuszczoną na tę podstawę, używamy podstawowego wzoru: Pole = ¹/₂ * a * h.
• Jeśli znamy długości wszystkich trzech boków trójkąta, używamy wzoru Herona: Pole = √[s(s-a)(s-b)(s-c)].
• Jeśli znamy długości dwóch boków i miarę kąta między nimi, używamy wzoru z wykorzystaniem sinusa kąta: Pole = ¹/₂ * a * b * sin(γ).

Pamiętaj, że każdy trójkąt ma trzy podstawy i trzy wysokości, więc możesz wybrać dowolną parę podstawa-wysokość, aby obliczyć jego pole, jeśli używasz podstawowego wzoru. Analogicznie, w przypadku wzoru z sinusem, możesz wybrać dowolne dwa boki i kąt między nimi.

Praktyczne Zastosowania Wzoru na Pole Trójkąta

Wzór na pole trójkąta znajduje szerokie zastosowanie w różnych dziedzinach życia, od matematyki i fizyki po inżynierię i architekturę.

• Geodezja i kartografia: Obliczanie powierzchni działek i map.
• Architektura i budownictwo: Projektowanie konstrukcji dachów, ścian i innych elementów budynków.
• Inżynieria: Obliczanie sił działających na konstrukcje trójkątne, takie jak mosty.
• Gry komputerowe i grafika 3D: Tworzenie realistycznych modeli i animacji.
• Żeglarstwo: Obliczanie powierzchni żagli.

Przykład: Wyobraź sobie, że chcesz pomalować ścianę w kształcie trójkąta. Aby obliczyć, ile farby potrzebujesz, musisz najpierw obliczyć powierzchnię ściany, czyli pole trójkąta. Wystarczy zmierzyć długość podstawy i wysokość ściany, a następnie zastosować podstawowy wzór na pole trójkąta.

Podsumowanie

Obliczanie pola trójkąta nie musi być trudne. Znając odpowiedni wzór i umiejętnie go stosując, możemy z łatwością rozwiązywać problemy związane z powierzchnią trójkątów. Pamiętaj o trzech głównych wzorach: podstawowym wzorze, wzorze Herona i wzorze z wykorzystaniem sinusa kąta. Wybierz ten, który najlepiej pasuje do dostępnych danych. Mam nadzieję, że ten artykuł pomógł Ci zrozumieć wzór na pole trójkąta i pokazał, jak go praktycznie zastosować. Teraz możesz śmiało przystąpić do rozwiązywania zadań i wykorzystywać tę wiedzę w życiu codziennym!