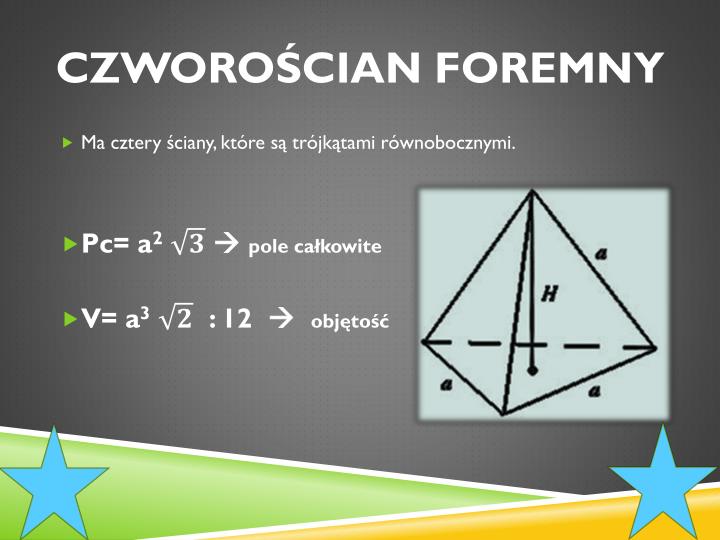
Jaką Wysokość Będzie Miał Szkielet Czworościanu Foremnego

Dzień dobry wszystkim! Dziś odpowiem na bardzo ciekawe pytanie: jaką wysokość będzie miał szkielet czworościanu foremnego? To zagadnienie z geometrii przestrzennej, które na pierwszy rzut oka może wydawać się skomplikowane, ale postaram się wszystko wytłumaczyć krok po kroku, w sposób prosty i zrozumiały.

Czworościan foremny, nazywany też tetraedrem, to bryła, której wszystkie ściany są trójkątami równobocznymi. To taka piramida o podstawie trójkątnej, gdzie każda ściana wygląda identycznie. Aby obliczyć wysokość szkieletu czworościanu, musimy sobie wyobrazić, co to właściwie znaczy. Szkielet, to tak jakbyśmy mieli czworościan zbudowany z samych krawędzi, bez wypełnienia ścianami. Więc, wysokość szkieletu to odległość od wierzchołka (najwyższego punktu) do płaszczyzny podstawy.

Obliczanie Wysokości Czworościanu Foremnego

Załóżmy, że długość krawędzi naszego czworościanu foremnego wynosi "a". To jest nasza bazowa informacja. Potrzebujemy wzoru, który powiąże długość krawędzi z wysokością. Ten wzór to:

h = (a√6) / 3

Gdzie:

• h - to wysokość czworościanu foremnego
• a - to długość krawędzi czworościanu foremnego
• √6 - to pierwiastek kwadratowy z 6

Czyli, żeby obliczyć wysokość, musimy pomnożyć długość krawędzi przez pierwiastek z 6, a następnie podzielić przez 3.

Przykład:

Powiedzmy, że mamy czworościan foremny o krawędzi długości 5 cm. Chcemy obliczyć jego wysokość.

1. Podstawiamy wartość "a" do wzoru: h = (5 * √6) / 3
2. Obliczamy pierwiastek z 6 (w przybliżeniu): √6 ≈ 2.449
3. Mnożymy: 5 * 2.449 ≈ 12.245
4. Dzielimy: 12.245 / 3 ≈ 4.082

Więc, wysokość tego czworościanu foremnego wynosi około 4.082 cm.

Kolejny przykład:

Załóżmy, że krawędź czworościanu ma długość 10 cm.

1. Podstawiamy do wzoru: h = (10 * √6) / 3
2. Obliczamy pierwiastek z 6: √6 ≈ 2.449
3. Mnożymy: 10 * 2.449 ≈ 24.49
4. Dzielimy: 24.49 / 3 ≈ 8.163

Wysokość takiego czworościanu to około 8.163 cm.

Jeszcze jeden przykład:

Krawędź czworościanu ma długość 2 cm.

1. Podstawiamy: h = (2 * √6) / 3
2. Obliczamy pierwiastek z 6: √6 ≈ 2.449
3. Mnożymy: 2 * 2.449 ≈ 4.898
4. Dzielimy: 4.898 / 3 ≈ 1.633

Wysokość wynosi około 1.633 cm.

Jak widzicie, wystarczy znać długość krawędzi i zastosować prosty wzór, aby obliczyć wysokość czworościanu foremnego. Można to zrobić ręcznie, używając kalkulatora, albo nawet arkusza kalkulacyjnego.

Warto pamiętać, że wynik, który otrzymujemy, jest przybliżony, ponieważ pierwiastek z 6 jest liczbą niewymierną, co oznacza, że ma nieskończone rozwinięcie dziesiętne. Im więcej miejsc po przecinku weźmiemy pod uwagę, tym dokładniejszy będzie wynik.

Praktyczne zastosowanie:

Obliczanie wysokości czworościanu foremnego może się przydać w różnych sytuacjach. Na przykład, jeśli projektujemy konstrukcję, która ma kształt czworościanu, musimy znać jego wymiary, aby upewnić się, że zmieści się w danym miejscu. Albo, jeśli chcemy obliczyć objętość czworościanu, potrzebujemy znać jego wysokość.

Podsumowanie:

Obliczanie wysokości szkieletu czworościanu foremnego jest proste, jeśli znamy długość jego krawędzi. Używamy do tego wzoru h = (a√6) / 3. Pamiętajcie, że √6 to w przybliżeniu 2.449. Podstawiamy wartość krawędzi, wykonujemy obliczenia i otrzymujemy wynik. Mam nadzieję, że teraz już wiecie, jak to zrobić! A jeśli macie jakieś pytania, śmiało pytajcie! Zawsze chętnie pomogę.

Pamiętajcie, że geometria przestrzenna to bardzo ciekawa dziedzina matematyki. Warto poświęcić jej trochę czasu, bo pozwala nam lepiej rozumieć świat wokół nas. Powodzenia w dalszej nauce!