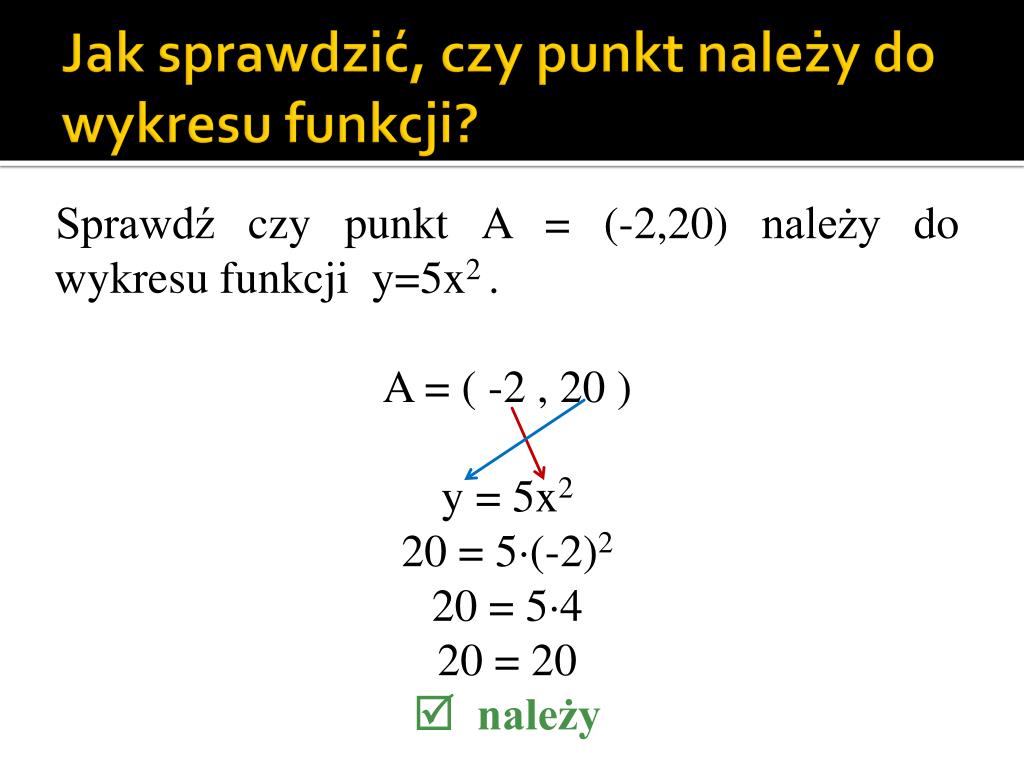Jak Sprawdzić Czy Dany Punkt Należy Do Wykresu Funkcji

Funkcja to jedno z podstawowych pojęć w matematyce. Często reprezentowana jest graficznie, tworząc wykres na układzie współrzędnych. Zadaniem, które często spotykamy, jest sprawdzenie, czy konkretny punkt należy do tego wykresu. Wbrew pozorom, jest to zadanie proste i bazuje na fundamentalnej definicji funkcji. Poniżej przedstawiam szczegółowy przewodnik, jak to zrobić krok po kroku.

Mając daną funkcję, zazwyczaj przedstawioną wzorem, na przykład f(x) = x² + 2x - 1, oraz punkt o współrzędnych (a, b), chcemy ustalić, czy ten punkt leży na wykresie tej funkcji.

Pierwszym krokiem jest podstawienie wartości x z naszego punktu, czyli a, do wzoru funkcji. W ten sposób obliczamy wartość funkcji dla tego konkretnego x.

Następnie, porównujemy wynik obliczeń, czyli f(a), z wartością y naszego punktu, czyli b. Jeśli f(a) = b, oznacza to, że punkt (a, b) leży na wykresie funkcji. W przeciwnym przypadku, punkt nie należy do wykresu.

Przykłady ilustrujące proces:

Weźmy funkcję f(x) = 3x - 5 i punkt (2, 1). Podstawiamy x = 2 do wzoru funkcji:

f(2) = 3 * 2 - 5 = 6 - 5 = 1

Otrzymaliśmy f(2) = 1. Ponieważ wartość y punktu to również 1, czyli b = 1, stwierdzamy, że f(2) = b. Zatem punkt (2, 1) należy do wykresu funkcji f(x) = 3x - 5.

Kolejny przykład: funkcja g(x) = x² + 1 i punkt (-1, 0). Podstawiamy x = -1 do wzoru funkcji:

g(-1) = (-1)² + 1 = 1 + 1 = 2

Otrzymaliśmy g(-1) = 2. Wartość y punktu wynosi 0, czyli b = 0. Widzimy, że g(-1) ≠ b. W związku z tym, punkt (-1, 0) nie należy do wykresu funkcji g(x) = x² + 1.

Rozważmy teraz funkcję h(x) = √x i punkt (4, 2). Pamiętajmy, że dziedziną tej funkcji są liczby nieujemne. Podstawiamy x = 4 do wzoru funkcji:

h(4) = √4 = 2

Otrzymaliśmy h(4) = 2. Wartość y punktu to również 2, czyli b = 2. Zatem h(4) = b. Punkt (4, 2) należy do wykresu funkcji h(x) = √x.

Jeszcze jeden przykład, funkcja k(x) = |x - 3| i punkt (1, 2). Podstawiamy x = 1 do wzoru funkcji:

k(1) = |1 - 3| = |-2| = 2

Otrzymaliśmy k(1) = 2. Wartość y punktu wynosi 2, czyli b = 2. Zatem k(1) = b. Punkt (1, 2) należy do wykresu funkcji k(x) = |x - 3|.

Funkcje Zdefiniowane Przedziałami

Sprawa komplikuje się nieco, gdy mamy do czynienia z funkcją zdefiniowaną przedziałami. W takim przypadku, zanim podstawimy wartość x do odpowiedniego wzoru, musimy najpierw ustalić, do którego przedziału należy nasz x.

Załóżmy, że mamy funkcję:

*f(x) = { x + 1, dla x < 0 { x² , dla x ≥ 0

i punkt (-2, -1). Wartość x naszego punktu to -2, która jest mniejsza od 0. Zatem, korzystamy z pierwszego wzoru:

f(-2) = -2 + 1 = -1

Otrzymaliśmy f(-2) = -1. Wartość y punktu to -1, czyli b = -1. Zatem f(-2) = b. Punkt (-2, -1) należy do wykresu funkcji.

Kolejny przykład: funkcja zdefiniowana przedziałami jak wyżej i punkt (1, 1). Wartość x naszego punktu to 1, która jest większa lub równa 0. Zatem, korzystamy z drugiego wzoru:

f(1) = 1² = 1

Otrzymaliśmy f(1) = 1. Wartość y punktu to 1, czyli b = 1. Zatem f(1) = b. Punkt (1, 1) należy do wykresu funkcji.

Ostatni przykład: funkcja zdefiniowana przedziałami jak wyżej i punkt (0, 2). Wartość x naszego punktu to 0, która jest większa lub równa 0. Zatem, korzystamy z drugiego wzoru:

f(0) = 0² = 0

Otrzymaliśmy f(0) = 0. Wartość y punktu to 2, czyli b = 2. Zatem f(0) ≠ b. Punkt (0, 2) nie należy do wykresu funkcji.

Funkcje Uwikłane

Czasami funkcja nie jest dana w postaci jawnej y = f(x), ale w postaci uwikłanej, np. x² + y² = 25. W takim przypadku, aby sprawdzić, czy punkt należy do wykresu, musimy podstawić zarówno x, jak i y do równania i sprawdzić, czy równość jest spełniona.

Rozważmy równanie x² + y² = 25 (jest to równanie okręgu o środku w punkcie (0,0) i promieniu 5) i punkt (3, 4). Podstawiamy x = 3 i y = 4 do równania:

3² + 4² = 9 + 16 = 25

Równość jest spełniona, zatem punkt (3, 4) należy do wykresu.

Rozważmy to samo równanie x² + y² = 25 i punkt (1, 2). Podstawiamy x = 1 i y = 2 do równania:

1² + 2² = 1 + 4 = 5

5 ≠ 25, więc równość nie jest spełniona. Punkt (1, 2) nie należy do wykresu.

Podsumowanie

Sprawdzanie, czy dany punkt należy do wykresu funkcji, jest zadaniem polegającym na podstawieniu wartości x punktu do wzoru funkcji i porównaniu wyniku z wartością y punktu. W przypadku funkcji zdefiniowanych przedziałami, należy najpierw ustalić, do którego przedziału należy x. W przypadku funkcji uwikłanych, podstawiamy zarówno x, jak i y do równania i sprawdzamy, czy równość jest spełniona. Pamiętając o tych prostych krokach, można z łatwością rozwiązać to zadanie. Ważne jest, aby precyzyjnie wykonywać obliczenia i zwracać uwagę na dziedzinę funkcji, szczególnie w przypadku funkcji takich jak pierwiastek kwadratowy czy logarytm. W przypadku funkcji z wartością bezwzględną, należy pamiętać o jej definicji. Zrozumienie tych podstawowych koncepcji pozwala na pewne poruszanie się po świecie funkcji i ich wykresów.

Wykorzystanie programów komputerowych

Obecnie, istnieje wiele programów komputerowych oraz kalkulatorów graficznych, które mogą pomóc w sprawdzeniu, czy punkt należy do wykresu funkcji. Wystarczy wprowadzić wzór funkcji oraz współrzędne punktu, a program sam obliczy wartość funkcji w danym punkcie i porówna ją z wartością y. Przykładem może być program GeoGebra, który jest darmowy i dostępny online. Korzystanie z takich narzędzi może znacznie przyspieszyć i ułatwić proces sprawdzania, szczególnie w przypadku bardziej skomplikowanych funkcji. Jednak, należy pamiętać, że programy te są tylko narzędziem pomocniczym, a zrozumienie podstawowych zasad jest kluczowe do prawidłowej interpretacji wyników. Znajomość tego procesu pomaga w głębszym zrozumieniu pojęcia funkcji i jej reprezentacji graficznej.