Jak Sie Oblicza Pole Prostokąta
Zastanawiałeś się kiedyś, jak obliczyć, ile farby potrzebujesz do pomalowania ściany w pokoju? A może planujesz ogródek i chcesz wiedzieć, ile miejsca zajmą Twoje grządki? W obu tych sytuacjach (i wielu innych!) przyda się umiejętność obliczania pola prostokąta. Ten artykuł jest skierowany do każdego, kto chce w prosty i zrozumiały sposób nauczyć się tej podstawowej umiejętności matematycznej. Niezależnie od tego, czy jesteś uczniem, studentem, majsterkowiczem, czy po prostu osobą ciekawą świata – zapraszam do lektury!
Czym właściwie jest prostokąt?
Zanim przejdziemy do obliczeń, upewnijmy się, że wszyscy wiemy, czym jest prostokąt. Prostokąt to czworokąt, który ma cztery kąty proste (każdy kąt ma 90 stopni). Charakteryzuje się tym, że przeciwległe boki są równe i równoległe.
Spójrzmy na cechy definiujące prostokąt:
- Cztery kąty proste (90 stopni każdy).
- Dwie pary boków równoległych i równej długości.
- Przeciwległe boki są równe.
Przykłady prostokątów w naszym otoczeniu to:
- Ekran telefonu
- Strona książki
- Drzwi
- Blat stołu (w wielu przypadkach)
Czym jest pole powierzchni?
Pole powierzchni to miara, która określa, ile dwuwymiarowej przestrzeni zajmuje dana figura. Możemy sobie wyobrazić, że wypełniamy wnętrze figury małymi kwadratami o boku jednostkowym (np. 1 cm, 1 m). Pole powierzchni to liczba tych kwadratów potrzebnych do całkowitego pokrycia figury. Jednostką pola powierzchni jest najczęściej centymetr kwadratowy (cm²), metr kwadratowy (m²) lub kilometr kwadratowy (km²).
Wzór na pole prostokąta – prostota w czystej postaci!
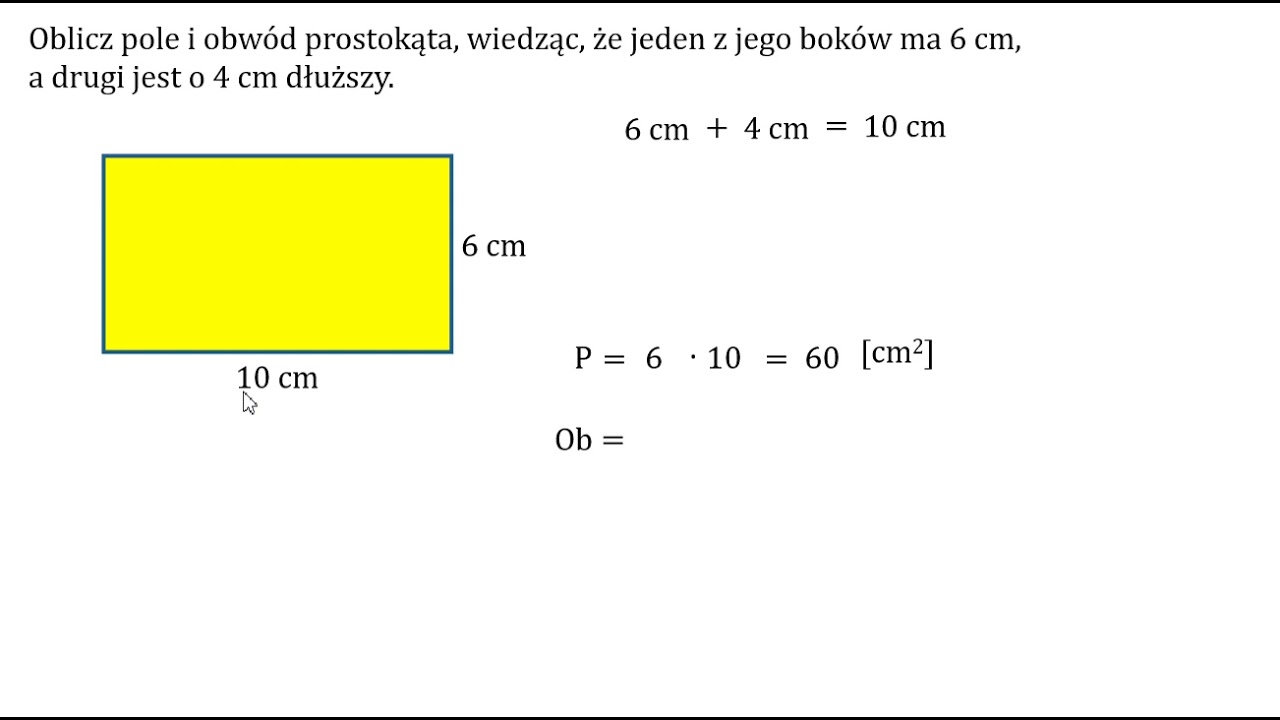
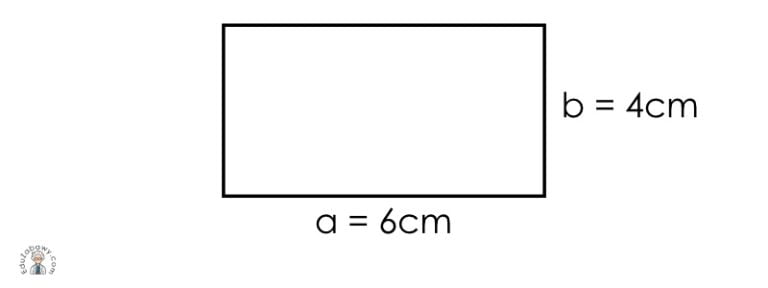
Obliczenie pola prostokąta jest niezwykle proste! Potrzebujemy tylko znać długość dwóch jego boków – zazwyczaj oznaczanych jako a i b.
Wzór na pole prostokąta to:
Pole = a * b
Gdzie:
- a to długość jednego boku prostokąta.
- b to długość drugiego boku prostokąta.
Innymi słowy, aby obliczyć pole prostokąta, wystarczy pomnożyć długość jednego boku przez długość drugiego boku!
Przykłady w praktyce – liczymy razem!
Przykład 1: Obliczanie pola dywanu
Wyobraźmy sobie, że chcemy kupić dywan do salonu. Dywan ma kształt prostokąta o wymiarach 3 metry na 4 metry. Jakie jest pole tego dywanu?
Krok 1: Określamy długości boków:
- a = 3 metry
- b = 4 metry
Krok 2: Stosujemy wzór na pole prostokąta:
Pole = a * b = 3 metry * 4 metry = 12 metrów kwadratowych
Odpowiedź: Pole dywanu wynosi 12 m².
Przykład 2: Obliczanie pola działki
Pan Kowalski kupił działkę pod budowę domu. Działka ma kształt prostokąta o wymiarach 20 metrów na 30 metrów. Jakie jest pole tej działki?
Krok 1: Określamy długości boków:
- a = 20 metrów
- b = 30 metrów
Krok 2: Stosujemy wzór na pole prostokąta:
Pole = a * b = 20 metrów * 30 metrów = 600 metrów kwadratowych
Odpowiedź: Pole działki wynosi 600 m².
Przykład 3: Obliczanie pola ekranu telefonu
Ekran Twojego smartfona ma wymiary 6 cm na 13 cm. Oblicz jego powierzchnię.
Krok 1: Określamy długości boków:
- a = 6 cm
- b = 13 cm
Krok 2: Stosujemy wzór na pole prostokąta:
Pole = a * b = 6 cm * 13 cm = 78 cm²
Odpowiedź: Powierzchnia ekranu Twojego telefonu wynosi 78 cm².
Praktyczne zastosowania obliczania pola prostokąta
Umiejętność obliczania pola prostokąta przydaje się w wielu sytuacjach w życiu codziennym. Oto kilka przykładów:
- Budownictwo i remonty: Obliczanie powierzchni ścian do pomalowania, podłóg do wyłożenia, dachów do pokrycia.
- Ogrodnictwo: Obliczanie powierzchni rabat kwiatowych, trawników, grządek warzywnych.
- Krawiectwo: Obliczanie ilości materiału potrzebnego do uszycia ubrania, obrusu, zasłon.
- Projektowanie wnętrz: Obliczanie powierzchni pomieszczeń, dobieranie odpowiednich mebli, dywanów.
- Geometria: Rozwiązywanie zadań matematycznych związanych z figurami geometrycznymi.
Porady i wskazówki
- Uważaj na jednostki! Zawsze upewnij się, że długości boków są podane w tej samej jednostce (np. metrach, centymetrach). Jeśli są podane w różnych jednostkach, musisz je najpierw przeliczyć.
- Sprawdź wynik! Po obliczeniu pola, zastanów się, czy wynik wydaje się sensowny. Czy pole dywanu o wymiarach 1 metr na 2 metry może wynosić 20 m²? Raczej nie!
- Użyj kalkulatora! Jeśli masz do czynienia z dużymi liczbami lub skomplikowanymi wymiarami, nie krępuj się użyć kalkulatora.
- Ćwicz! Im więcej będziesz ćwiczył obliczanie pola prostokąta, tym łatwiej i szybciej będziesz to robił. Możesz zacząć od prostych przykładów, a następnie stopniowo przechodzić do bardziej skomplikowanych zadań.
- Pamiętaj, że kwadrat jest szczególnym przypadkiem prostokąta, gdzie wszystkie boki są równe. Więc pole kwadratu o boku *a* wynosi *a* * *a* czyli a².
Podsumowanie – już wiesz wszystko!
Gratulacje! Właśnie nauczyłeś się, jak obliczać pole prostokąta. Pamiętaj, że wystarczy pomnożyć długość jednego boku przez długość drugiego boku. Teraz możesz bez problemu obliczyć powierzchnię dywanu, działki, ściany, a nawet ekranu swojego telefonu. Mam nadzieję, że ten artykuł okazał się pomocny i że wiedza zdobyta tutaj przyda Ci się w życiu codziennym. Powodzenia w dalszych matematycznych (i nie tylko!) przygodach!
Pamiętaj: Matematyka jest wszędzie wokół nas! Ucząc się podstawowych zagadnień, takich jak obliczanie pola prostokąta, otwieramy sobie drzwi do lepszego zrozumienia świata.