Jak Się Liczy Pole Trójkąta

Zapewne nieraz zadawałeś sobie pytanie: "Jak obliczyć pole trójkąta?" Być może potrzebujesz tego do projektu szkolnego, a może do planowania ogrodu, w którym chcesz postawić szklarnię o nietypowym kształcie. Niezależnie od powodu, zrozumienie, jak to zrobić, jest naprawdę przydatne. Matematyka potrafi budzić strach, ale obiecuję, że obliczanie pola trójkąta wcale nie musi być trudne! Razem przejdziemy przez kilka prostych metod, które pomogą Ci opanować tę umiejętność.

Często, gdy słyszymy słowo "matematyka", od razu myślimy o nudnych wzorach i skomplikowanych obliczeniach. Ale pomyśl o tym inaczej: wiedza o tym, jak obliczyć pole trójkąta, to narzędzie, które możesz wykorzystać w wielu sytuacjach. Od obliczania ilości materiału potrzebnego do uszycia żagla, po planowanie układu mebli w pokoju o nietypowym kształcie. To praktyczna wiedza, która może Ci się przydać na co dzień!

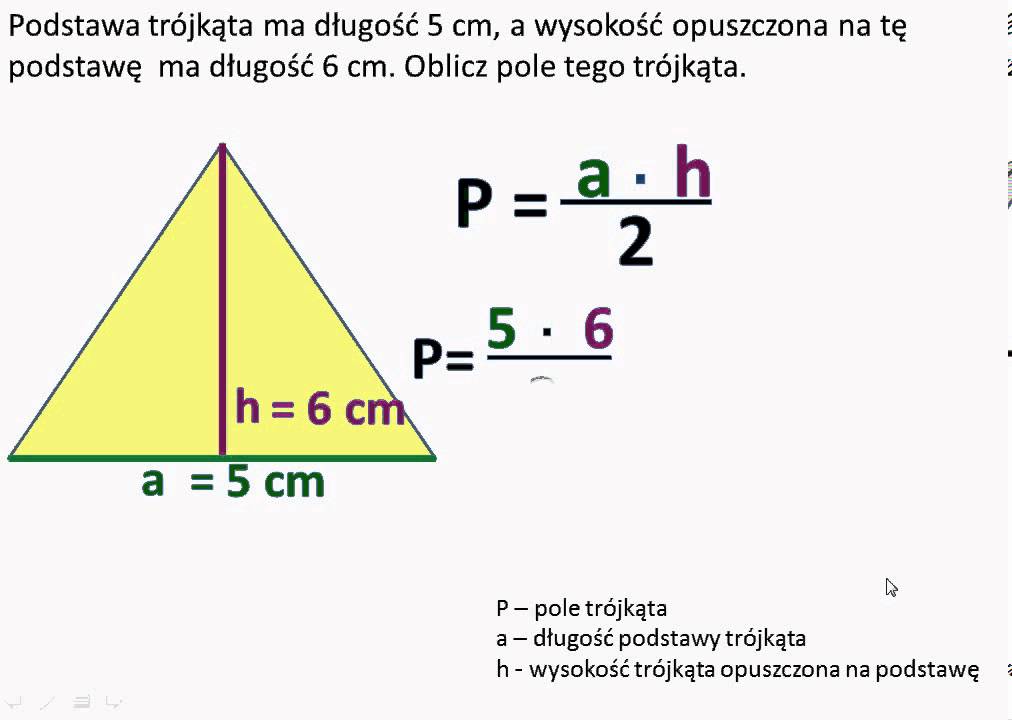
Podstawowy Wzór: Podstawa Razy Wysokość Podzielone Przez Dwa

Najbardziej znanym i najczęściej używanym wzorem na pole trójkąta jest:

Pole = (podstawa * wysokość) / 2

Ale co to właściwie znaczy? Wyobraź sobie trójkąt. Podstawa to jeden z jego boków (zazwyczaj ten, który leży "na dole"). Wysokość to odległość od wierzchołka naprzeciwko podstawy do samej podstawy, mierzona pod kątem prostym (90 stopni). Innymi słowy, to linia prosta, która idzie od wierzchołka do podstawy, tworząc kąt prosty.

Przykład: Załóżmy, że masz trójkąt, którego podstawa ma 10 cm długości, a wysokość wynosi 5 cm. W takim przypadku:

Pole = (10 cm * 5 cm) / 2 = 25 cm²

Czyli pole tego trójkąta wynosi 25 centymetrów kwadratowych.

Kiedy Używać Tego Wzoru?

• Kiedy znamy długość podstawy i wysokość trójkąta. To najważniejszy warunek. Jeśli znasz te dwie wartości, ten wzór jest najprostszy i najszybszy do użycia.
• W przypadku trójkątów prostokątnych. W trójkącie prostokątnym, jedna z przyprostokątnych jest podstawą, a druga jest wysokością.
• Przy rozwiązywaniu prostych zadań szkolnych. To klasyczny wzór, który jest uczony na lekcjach matematyki.

Wzór Herona: Kiedy Znamy Długości Wszystkich Boków

Co zrobić, gdy nie znamy wysokości, ale za to znamy długości wszystkich trzech boków trójkąta? Wtedy z pomocą przychodzi wzór Herona. Brzmi strasznie, ale tak naprawdę nie jest taki zły!

Wzór Herona wygląda tak:

Pole = √[p(p-a)(p-b)(p-c)]

Gdzie:

• a, b, c to długości boków trójkąta
• p to połowa obwodu trójkąta, czyli p = (a + b + c) / 2

Zacznijmy od obliczenia połowy obwodu (p). Po prostu dodaj do siebie długości wszystkich boków i podziel wynik przez 2. Następnie, podstaw wartości a, b, c i p do wzoru Herona i oblicz pole. Pamiętaj, że symbol √ oznacza pierwiastek kwadratowy.

Przykład: Załóżmy, że masz trójkąt o bokach długości a = 3 cm, b = 4 cm, c = 5 cm.

1. Oblicz p: p = (3 + 4 + 5) / 2 = 6
2. Podstaw do wzoru Herona: Pole = √[6(6-3)(6-4)(6-5)] = √[6 * 3 * 2 * 1] = √36 = 6

Czyli pole tego trójkąta wynosi 6 centymetrów kwadratowych.

Kiedy Używać Wzoru Herona?

• Kiedy znamy długości wszystkich trzech boków trójkąta. To jedyny warunek.
• Kiedy nie możemy łatwo obliczyć wysokości trójkąta. W niektórych przypadkach, wyznaczenie wysokości może być skomplikowane.

Trygonometria w Służbie Pola Trójkąta

Jeśli znasz trochę trygonometrii, możesz użyć kolejnego wzoru na pole trójkąta:

Pole = (1/2) * a * b * sin(γ)

Gdzie:

• a i b to długości dwóch boków trójkąta
• γ (gamma) to kąt między tymi dwoma bokami
• sin(γ) to sinus kąta γ

Ten wzór jest szczególnie przydatny, gdy znasz długości dwóch boków i kąt między nimi. Musisz jedynie znaleźć sinus kąta (możesz użyć kalkulatora naukowego) i podstawić wartości do wzoru.

Przykład: Załóżmy, że masz trójkąt, w którym bok a ma 8 cm, bok b ma 6 cm, a kąt między nimi (γ) wynosi 30 stopni. Sinus kąta 30 stopni wynosi 0.5.

Pole = (1/2) * 8 cm * 6 cm * 0.5 = 12 cm²

Czyli pole tego trójkąta wynosi 12 centymetrów kwadratowych.

Kiedy Używać Wzoru Trygonometrycznego?

• Kiedy znamy długości dwóch boków i kąt między nimi. To kluczowy warunek.
• Kiedy mamy dostęp do funkcji sinus na kalkulatorze. Bez tego, obliczenie sinusa kąta może być trudne.
• W zadaniach, w których podane są kąty i boki trójkąta. Często w tego typu zadaniach, wzór trygonometryczny jest najprostszy w użyciu.

Przykłady Zastosowań w Życiu Codziennym

Pomyśl o żaglu na łodzi. Ma kształt trójkąta! Aby obliczyć, ile materiału potrzebujesz, musisz znać jego pole. Architekci używają geometrii, w tym obliczania pól trójkątów, do projektowania budynków o nietypowych kształtach. Rzemieślnicy, którzy wykonują mozaiki, również często wykorzystują tę wiedzę. Ogrodnicy mogą użyć tej wiedzy do zaprojektowania grządek w kształcie trójkątów.

• Budownictwo: Obliczanie ilości materiałów potrzebnych do pokrycia dachu w kształcie trójkąta.
• Projektowanie wnętrz: Planowanie rozmieszczenia mebli w pomieszczeniu o nietypowym kształcie.
• Szycie: Obliczanie ilości materiału potrzebnego do uszycia elementu ubrania w kształcie trójkąta.
• Grafika komputerowa: Trójkąty są podstawą modelowania 3D. Obliczanie ich pól jest ważne dla renderingu.

Potencjalne Trudności i Jak Je Pokonać

Czasami możesz mieć problem z określeniem, który bok jest podstawą, a który wysokością. Pamiętaj, że wysokość zawsze musi być prostopadła do podstawy. Jeśli masz trójkąt rozwartokątny, wysokość może wypadać poza jego obręb. Wzór Herona może wydawać się skomplikowany, ale tak naprawdę to tylko kwestia podstawienia wartości do wzoru i wykonania obliczeń. Używaj kalkulatora, aby uniknąć błędów!

Ważne jest również, aby pamiętać o jednostkach. Jeśli podstawa i wysokość są podane w centymetrach, pole będzie w centymetrach kwadratowych. Jeśli są podane w metrach, pole będzie w metrach kwadratowych. Zawsze upewnij się, że używasz odpowiednich jednostek!

Co z Innymi Wzorami i Metodami?

Istnieją inne, bardziej zaawansowane metody obliczania pola trójkąta, na przykład przy użyciu wektorów. Jednak te metody są zwykle używane w bardziej zaawansowanej matematyce i fizyce. Dla większości zastosowań, wzory omówione powyżej są w zupełności wystarczające.

Przeciwnicy prostych metod argumentują, że są one niedokładne w niektórych przypadkach (np. trójkąty bardzo "płaskie"). Jednak w praktycznych zastosowaniach, różnice są zwykle niewielkie i nie mają znaczącego wpływu na wynik. Ponadto, można zwiększyć dokładność, używając kalkulatora z większą liczbą miejsc po przecinku.

Podsumowanie i Co Dalej?

Gratulacje! Przeszliśmy razem przez kilka sposobów na obliczenie pola trójkąta. Pamiętaj, że najważniejsza jest praktyka. Spróbuj rozwiązać kilka zadań, aby utrwalić swoją wiedzę. Poszukaj zadań online lub w podręczniku. Z czasem, obliczanie pola trójkąta stanie się dla Ciebie łatwe i intuicyjne.

Teraz, gdy znasz różne metody obliczania pola trójkąta, możesz wykorzystać tę wiedzę w wielu sytuacjach. Od planowania ogrodu, po rozwiązywanie zadań szkolnych. Matematyka wcale nie musi być nudna! Możesz również spróbować dowiedzieć się więcej o geometrii i innych figurach geometrycznych. Świat matematyki jest fascynujący i pełen niespodzianek!

Czy masz teraz pomysł, gdzie wykorzystasz zdobytą wiedzę? Spróbuj rozwiązać kilka zadań praktycznych i zobacz, jak wiele możesz zdziałać! Powodzenia!