Jak Sie Liczy Pole Prostokąta

Często spotykamy się z sytuacjami, gdzie obliczenie powierzchni wydaje się abstrakcyjną matematyką, oderwaną od rzeczywistości. Czy zastanawiałeś się kiedyś, po co właściwie uczyć się obliczania pola prostokąta? Czy to tylko kolejne zadanie domowe, czy coś więcej?

Zrozumienie obliczania pola prostokąta jest fundamentem dla wielu aspektów naszego życia, choć na pierwszy rzut oka może się to nie wydawać oczywiste. Wyobraź sobie remont mieszkania, układanie płytek w łazience, czy nawet zakup odpowiedniej ilości tapety. Bez znajomości obliczania pola, możemy łatwo przepłacić, kupując za dużo materiału, albo co gorsza – zabraknąć go w trakcie prac.

Po co właściwie liczyć pole prostokąta?

Obliczanie pola prostokąta nie jest tylko abstrakcyjną regułą. To praktyczna umiejętność, która przydaje się w wielu codziennych sytuacjach:

Remont i wystrój wnętrz: Obliczanie powierzchni podłogi, ścian, sufitów, aby kupić odpowiednią ilość farby, tapet, paneli, płytek.
Ogrodnictwo: Planowanie rabat kwiatowych, trawników, ścieżek – obliczanie potrzebnej ilości ziemi, nasion, kostki brukowej.
Budownictwo: Projektowanie domów, budynków – obliczanie powierzchni dachów, ścian, podłóg, aby oszacować koszty materiałów.
Rzemiosło: Tworzenie modeli, projektów, obrazów – obliczanie powierzchni potrzebnej do pokrycia materiałem.
Kupowanie dywanu: Dopasowanie dywanu do pokoju.
Zakup działki: Weryfikacja powierzchni działki.

Jak widzisz, zastosowań jest bardzo wiele. W każdym z tych przypadków, błąd w obliczeniach może prowadzić do strat finansowych, marnowania materiałów i frustracji. Dlatego warto poświęcić chwilę, aby dobrze zrozumieć, jak to się robi.

Jak obliczyć pole prostokąta – krok po kroku?

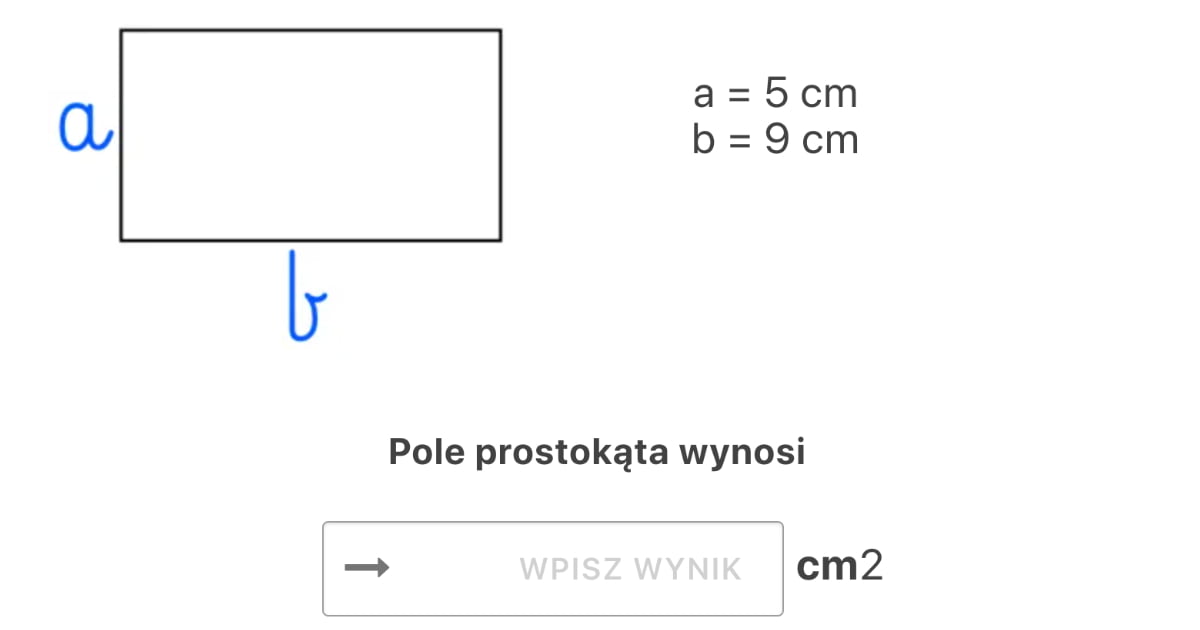
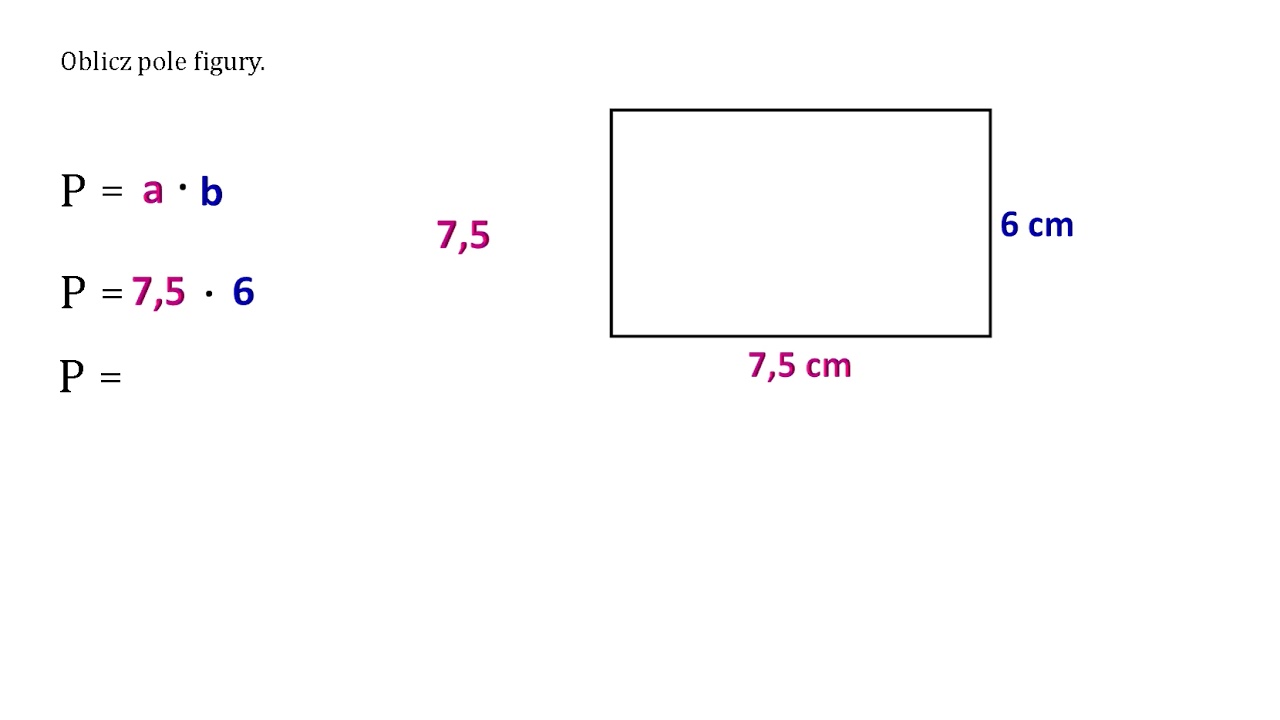
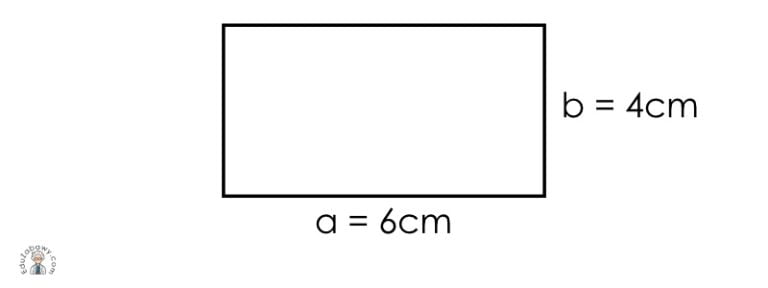
Obliczenie pola prostokąta jest bardzo proste. Potrzebujesz tylko znać długość jego dwóch sąsiednich boków – oznaczmy je jako a i b.

Wzór na pole prostokąta:

P = a * b

Gdzie:

P – pole prostokąta
a – długość jednego boku
b – długość drugiego boku

Przykład:

Wyobraźmy sobie, że mamy prostokąt o wymiarach: a = 5 cm i b = 8 cm.

Aby obliczyć jego pole, po prostu podstawiamy te wartości do wzoru:

P = 5 cm * 8 cm = 40 cm²

Czyli pole tego prostokąta wynosi 40 centymetrów kwadratowych.

Kluczowe elementy:

Jednostki: Pamiętaj o używaniu jednakowych jednostek dla obu boków. Jeśli jeden bok jest podany w centymetrach, a drugi w metrach, musisz najpierw zamienić je na tę samą jednostkę.
Mnożenie: Najważniejsze jest prawidłowe pomnożenie długości boków. Możesz użyć kalkulatora, aby uniknąć błędów.

Częste błędy i jak ich unikać

Mimo prostoty wzoru, przy obliczaniu pola prostokąta mogą wystąpić pewne błędy. Oto kilka najczęstszych i wskazówki, jak ich unikać:

Zapominanie o jednostkach: Zawsze zapisuj jednostki! Brak jednostki przy wyniku sprawia, że jest on bezwartościowy. Pamiętaj, że pole zawsze wyrażamy w jednostkach kwadratowych (np. cm², m², km²).
Używanie różnych jednostek: Jak już wspomniano, upewnij się, że oba boki są podane w tej samej jednostce. Jeśli nie, zamień je!
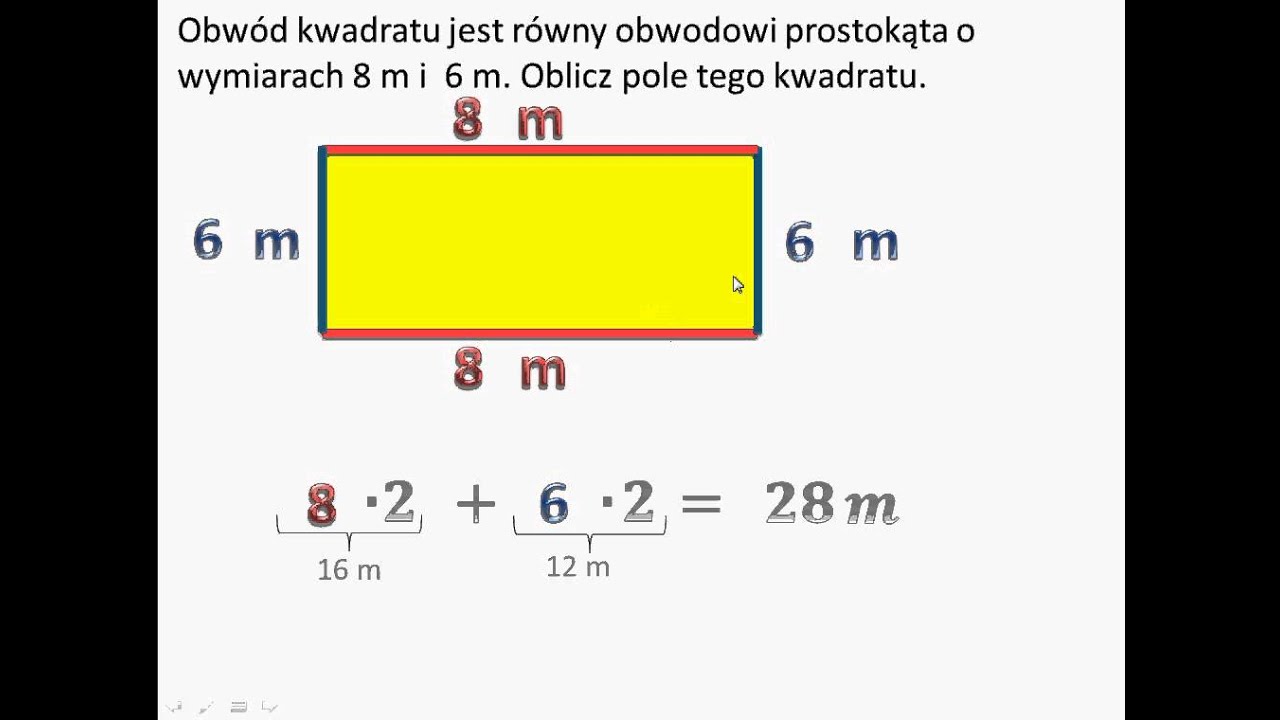
Mylenie obwodu z polem: Obwód to suma długości wszystkich boków, a pole to powierzchnia wewnątrz prostokąta. Nie myl tych pojęć!
Błędy w obliczeniach: Sprawdź obliczenia! Użyj kalkulatora lub poproś kogoś o sprawdzenie Twojego wyniku.

Counterpoints – co, jeśli mam nieregularny kształt?

To prawda, że nie wszystko w życiu ma idealny kształt prostokąta. Co zrobić, gdy mamy do czynienia z bardziej skomplikowanymi, nieregularnymi kształtami?

Istnieją różne metody radzenia sobie z takimi sytuacjami:

Podział na prostokąty: Spróbuj podzielić nieregularny kształt na mniejsze, prostsze figury, np. prostokąty i kwadraty. Oblicz pole każdej z nich osobno, a następnie zsumuj wyniki.
Metody przybliżone: W przypadku bardzo skomplikowanych kształtów, można użyć metod przybliżonych, np. metody trapezów lub metody Monte Carlo.
Użycie specjalistycznego oprogramowania: Istnieją programy komputerowe, które automatycznie obliczają pole nieregularnych kształtów na podstawie rysunku lub zdjęcia.

Jednak znajomość obliczania pola prostokąta jest nadal kluczowa, ponieważ stanowi podstawę do radzenia sobie z bardziej skomplikowanymi problemami.

Praktyczne przykłady zastosowania

Żeby jeszcze bardziej pokazać, jak przydatna jest ta umiejętność, przyjrzyjmy się kilku bardziej szczegółowym przykładom:

Remont pokoju

Chcesz pomalować ściany w swoim pokoju. Pokój ma wymiary 4 m x 3 m, a wysokość ścian wynosi 2,5 m. Ile farby musisz kupić?

Najpierw obliczamy powierzchnię ścian:

Dwie ściany mają wymiary 4 m x 2,5 m, więc ich łączna powierzchnia to 2 * (4 m * 2,5 m) = 20 m²
Dwie pozostałe ściany mają wymiary 3 m x 2,5 m, więc ich łączna powierzchnia to 2 * (3 m * 2,5 m) = 15 m²
Łączna powierzchnia wszystkich ścian to 20 m² + 15 m² = 35 m²

Teraz musisz sprawdzić na puszce z farbą, ile metrów kwadratowych pokrywa jeden litr farby. Załóżmy, że jeden litr farby wystarcza na 10 m².

Wtedy potrzebujesz 35 m² / 10 m²/litr = 3,5 litra farby.

W praktyce kupisz 4 litry, żeby mieć pewność, że starczy.

Układanie płytek w łazience

Chcesz ułożyć płytki na podłodze w łazience. Łazienka ma wymiary 2 m x 1,5 m. Ile płytek musisz kupić, jeśli każda płytka ma wymiary 20 cm x 20 cm?

Najpierw obliczamy powierzchnię podłogi:

P = 2 m * 1,5 m = 3 m²

Teraz obliczamy powierzchnię jednej płytki:

P = 20 cm * 20 cm = 400 cm² = 0,04 m²

Następnie dzielimy powierzchnię podłogi przez powierzchnię jednej płytki:

3 m² / 0,04 m²/płytkę = 75 płytek

W praktyce kupisz około 80 płytek, żeby mieć zapas na ewentualne docinanie i uszkodzenia.

Planowanie ogrodu

Chcesz założyć rabatę kwiatową w kształcie prostokąta. Masz do dyspozycji 5 metrów bieżących obrzeża. Jakie wymiary powinna mieć rabata, aby miała jak największe pole?

Tutaj wkraczamy w optymalizację, ale znajomość pola prostokąta jest nadal kluczowa.

Jeśli obwód rabaty to 5 metrów, to 2a + 2b = 5, gdzie a i b to długości boków. Możemy to uprościć do a + b = 2,5.

Pole rabaty to P = a * b.

Żeby zmaksymalizować pole, rabata powinna być jak najbardziej zbliżona do kwadratu. Czyli a = b = 1,25 m.

Wtedy pole rabaty wynosi P = 1,25 m * 1,25 m = 1,5625 m².

Jak widzisz, nawet planowanie ogrodu wymaga znajomości obliczania pola prostokąta!

Podsumowanie i co dalej?

Obliczanie pola prostokąta to fundamentalna umiejętność, która przydaje się w wielu aspektach życia – od remontu mieszkania, przez planowanie ogrodu, aż po projektowanie budynków. Mimo swojej prostoty, wymaga dokładności i zrozumienia jednostek.

Pamiętaj, że praktyka czyni mistrza. Im więcej będziesz ćwiczył obliczanie pola prostokąta, tym łatwiej i szybciej będziesz to robił.

Co możesz zrobić dalej?

Rozwiąż kilka zadań: Znajdź w Internecie zadania z obliczaniem pola prostokąta i spróbuj je rozwiązać.
Zastosuj wiedzę w praktyce: Spróbuj obliczyć pole pokoju, ogrodu, stołu – wszystkiego, co ma kształt prostokąta.
Pomóż komuś: Naucz kogoś obliczać pole prostokąta. Wyjaśnianie komuś zagadnień matematycznych to świetny sposób na utrwalenie wiedzy.

Czy potrafisz teraz wyobrazić sobie, jak znajomość obliczania pola prostokąta ułatwi Ci codzienne życie? Jakie projekty możesz zrealizować dzięki tej umiejętności?