Jak Sie Liczy Pole Graniastosłupa

Zastanawiałeś się kiedyś, ile materiału potrzeba na uszycie namiotu w kształcie graniastosłupa? A może jak dużo farby kupić, aby pomalować element architektoniczny o takiej formie? Znajomość obliczania pola powierzchni graniastosłupa jest kluczowa w wielu praktycznych sytuacjach. Ten artykuł jest dla Ciebie, jeśli chcesz zrozumieć, jak to zrobić – od podstawowych definicji, aż po bardziej złożone przykłady. Bez obaw, wszystko wyjaśnimy krok po kroku!

Czym jest graniastosłup? Podstawowe definicje

Zanim przejdziemy do obliczeń, upewnijmy się, że rozumiemy, czym właściwie jest graniastosłup. Graniastosłup to bryła geometryczna, która posiada dwie identyczne i równoległe podstawy (w kształcie wielokątów) połączone ścianami bocznymi, które są równoległobokami. Wyobraź sobie pudełko czekoladek – często ma formę graniastosłupa!

Kluczowe elementy graniastosłupa:

Podstawy: Dwa identyczne wielokąty, które definiują kształt graniastosłupa (np. trójkąty, kwadraty, pięciokąty).
Ściany boczne: Równoległoboki łączące odpowiadające sobie boki podstaw. W przypadku graniastosłupa prostego, ściany boczne są prostokątami.
Krawędzie: Linie, wzdłuż których stykają się ściany.
Wierzchołki: Punkty, w których zbiegają się krawędzie.

Rodzaje graniastosłupów:

Graniastosłup prosty: Ściany boczne są prostopadłe do podstaw.
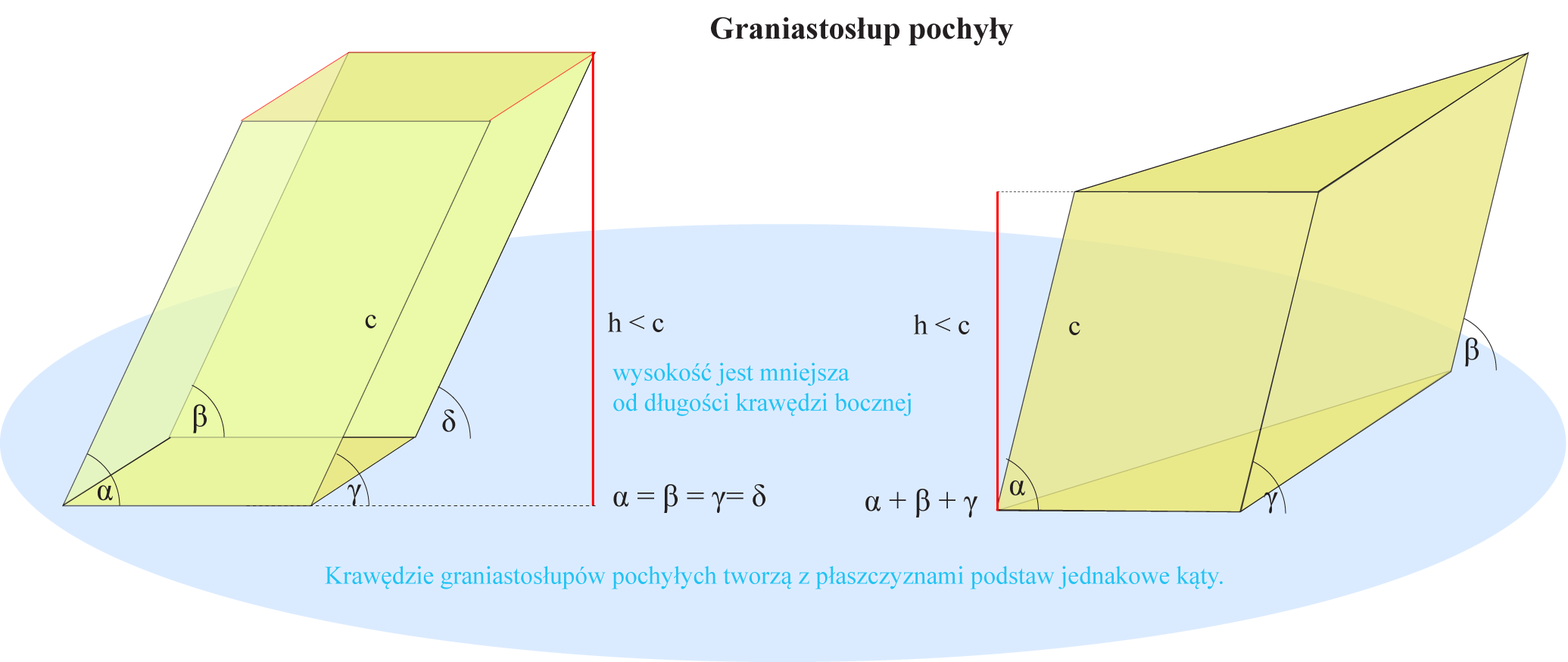
Graniastosłup pochyły: Ściany boczne nie są prostopadłe do podstaw.
Graniastosłup prawidłowy: Graniastosłup prosty, którego podstawą jest wielokąt foremny (np. trójkąt równoboczny, kwadrat, pięciokąt foremny).

Dlaczego warto znać wzory na pole powierzchni graniastosłupa?

Umiejętność obliczania pola powierzchni graniastosłupa przydaje się w wielu sytuacjach:

Architektura i budownictwo: Obliczanie ilości materiałów potrzebnych do budowy dachu, ścian lub innych elementów o kształcie graniastosłupa.
Projektowanie: Szacowanie kosztów produkcji opakowań, pudełek lub innych przedmiotów o kształcie graniastosłupa.
Inżynieria: Obliczanie powierzchni elementów konstrukcyjnych.
Życie codzienne: Określanie ilości farby potrzebnej do pomalowania przedmiotu o kształcie graniastosłupa, obliczanie ilości papieru potrzebnego do owinięcia prezentu.

Wzór na pole powierzchni całkowitej graniastosłupa

Aby obliczyć pole powierzchni całkowitej graniastosłupa, musimy zsumować pola wszystkich jego ścian – dwóch podstaw i ścian bocznych. Brzmi skomplikowanie? Spokojnie, wzór to ułatwi:

P_c = 2P_p + P_b

Gdzie:

P_c – Pole powierzchni całkowitej graniastosłupa.
P_p – Pole jednej podstawy graniastosłupa.
P_b – Pole powierzchni bocznej graniastosłupa (suma pól wszystkich ścian bocznych).

Teraz rozbijemy ten wzór na czynniki pierwsze i zobaczymy, jak obliczyć pole podstawy i pole powierzchni bocznej.

Obliczanie pola podstawy (P_p)

Kształt podstawy graniastosłupa może być różny – trójkąt, kwadrat, prostokąt, pięciokąt, sześciokąt, itd. Dlatego, aby obliczyć pole podstawy, musimy znać wzór na pole danego wielokąta.

Przykłady:

Podstawa w kształcie trójkąta: P_p = (a * h) / 2, gdzie 'a' to długość podstawy trójkąta, a 'h' to jego wysokość.
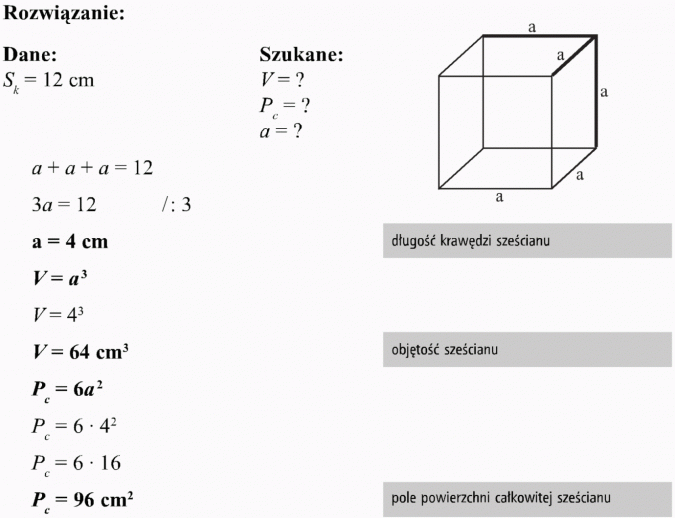
Podstawa w kształcie kwadratu: P_p = a², gdzie 'a' to długość boku kwadratu.
Podstawa w kształcie prostokąta: P_p = a * b, gdzie 'a' i 'b' to długości boków prostokąta.
Podstawa w kształcie sześciokąta foremnego: P_p = (3√3 * a²) / 2, gdzie 'a' to długość boku sześciokąta.

Pamiętaj! Wybierz odpowiedni wzór w zależności od kształtu podstawy graniastosłupa.

Obliczanie pola powierzchni bocznej (P_b)

Pole powierzchni bocznej to suma pól wszystkich ścian bocznych. W przypadku graniastosłupa prostego, ściany boczne są prostokątami. Wtedy:

P_b = Obwód podstawy * Wysokość graniastosłupa

Gdzie:

Obwód podstawy to suma długości wszystkich boków wielokąta, który jest podstawą graniastosłupa.
Wysokość graniastosłupa to odległość między podstawami.

Jeśli mamy do czynienia z graniastosłupem pochyłym, sytuacja jest nieco bardziej skomplikowana. Musimy obliczyć pole każdego równoległoboku oddzielnie i je zsumować.

Przykłady obliczania pola powierzchni graniastosłupa

Zobaczmy teraz, jak zastosować te wzory w praktyce. Przejdźmy przez kilka przykładów.

Przykład 1: Graniastosłup prosty trójkątny

Mamy graniastosłup prosty trójkątny, w którym podstawa jest trójkątem równobocznym o boku a = 5 cm. Wysokość graniastosłupa wynosi H = 10 cm. Oblicz pole powierzchni całkowitej.

Krok 1: Obliczamy pole podstawy (P_p)

Wzór na pole trójkąta równobocznego: P_p = (a²√3) / 4

P_p = (5²√3) / 4 = (25√3) / 4 ≈ 10.83 cm²

Krok 2: Obliczamy obwód podstawy

Obwód trójkąta równobocznego: O = 3a = 3 * 5 = 15 cm

Krok 3: Obliczamy pole powierzchni bocznej (P_b)

P_b = Obwód podstawy * Wysokość = 15 * 10 = 150 cm²

Krok 4: Obliczamy pole powierzchni całkowitej (P_c)

P_c = 2P_p + P_b = 2 * 10.83 + 150 = 21.66 + 150 = 171.66 cm²

Odpowiedź: Pole powierzchni całkowitej graniastosłupa wynosi około 171.66 cm².

Przykład 2: Graniastosłup prosty czworokątny (prostopadłościan)

Mamy prostopadłościan o wymiarach: a = 3 cm, b = 4 cm, H = 6 cm. Oblicz pole powierzchni całkowitej.

Krok 1: Obliczamy pole podstawy (P_p)

P_p = a * b = 3 * 4 = 12 cm²

Krok 2: Obliczamy obwód podstawy

Obwód prostokąta: O = 2(a + b) = 2(3 + 4) = 14 cm

Krok 3: Obliczamy pole powierzchni bocznej (P_b)

P_b = Obwód podstawy * Wysokość = 14 * 6 = 84 cm²

Krok 4: Obliczamy pole powierzchni całkowitej (P_c)

P_c = 2P_p + P_b = 2 * 12 + 84 = 24 + 84 = 108 cm²

Odpowiedź: Pole powierzchni całkowitej prostopadłościanu wynosi 108 cm².

Przykład 3: Graniastosłup prawidłowy sześciokątny

Rozważmy graniastosłup prawidłowy sześciokątny o boku podstawy a = 2 cm i wysokości H = 5 cm. Oblicz pole powierzchni całkowitej.

Krok 1: Obliczamy pole podstawy (P_p)

Wzór na pole sześciokąta foremnego: P_p = (3√3 * a²) / 2

P_p = (3√3 * 2²) / 2 = (3√3 * 4) / 2 = 6√3 ≈ 10.39 cm²

Krok 2: Obliczamy obwód podstawy

Obwód sześciokąta foremnego: O = 6a = 6 * 2 = 12 cm

Krok 3: Obliczamy pole powierzchni bocznej (P_b)

P_b = Obwód podstawy * Wysokość = 12 * 5 = 60 cm²

Krok 4: Obliczamy pole powierzchni całkowitej (P_c)

P_c = 2P_p + P_b = 2 * 10.39 + 60 = 20.78 + 60 = 80.78 cm²

Odpowiedź: Pole powierzchni całkowitej graniastosłupa wynosi około 80.78 cm².

Praktyczne wskazówki

Zawsze zaczynaj od określenia, jaki rodzaj graniastosłupa masz przed sobą. To pomoże Ci wybrać odpowiednie wzory.
Upewnij się, że wszystkie wymiary są podane w tej samej jednostce. Jeśli nie, przelicz je.
Sprawdź swoje obliczenia. Łatwo o pomyłkę, zwłaszcza przy bardziej skomplikowanych wzorach.
Zapisuj jednostki. Pamiętaj, że pole powierzchni wyrażamy w jednostkach kwadratowych (np. cm², m²).

Podsumowanie

Obliczanie pola powierzchni graniastosłupa może wydawać się trudne na początku, ale dzięki systematycznemu podejściu i znajomości wzorów, staje się to proste i przyjemne. Pamiętaj o podziale zadania na mniejsze kroki: obliczenie pola podstawy, obliczenie obwodu podstawy (jeśli potrzebny), obliczenie pola powierzchni bocznej, a na końcu obliczenie pola powierzchni całkowitej. Teraz, gdy znasz już teorię i widziałeś praktyczne przykłady, możesz śmiało zmierzyć się z każdym graniastosłupem! Wykorzystaj tę wiedzę w życiu codziennym i w pracy, a zobaczysz, jak bardzo jest przydatna.

Mamy nadzieję, że ten artykuł okazał się pomocny. Powodzenia w obliczeniach!