Jak Sie Dzieli Ulamki Zwykle

Czy kiedykolwiek zdarzyło Ci się piec ciasto i nagle okazało się, że musisz podzielić przepis na pół? Albo podzielić pizzę na równe kawałki dla większej grupy przyjaciół? W takich sytuacjach dzielenie ułamków zwykłych staje się nieocenione. Ten artykuł jest dedykowany wszystkim, którzy chcą zrozumieć i opanować tę ważną umiejętność matematyczną, niezależnie od tego, czy jesteś uczniem, studentem, rodzicem pomagającym dziecku w nauce, czy po prostu osobą chcącą odświeżyć swoją wiedzę.
Dlaczego dzielenie ułamków jest ważne?
Dzielenie ułamków zwykłych jest fundamentem wielu operacji matematycznych i ma szerokie zastosowanie w życiu codziennym. Zrozumienie tej zasady pozwala na:
- Rozwiązywanie problemów praktycznych: Jak wspomniano wcześniej, od gotowania po obliczanie proporcji w projektach budowlanych.
- Lepsze zrozumienie matematyki: Dzielenie ułamków jest bazą dla bardziej zaawansowanych koncepcji, takich jak równania i algebra.
- Rozwijanie umiejętności logicznego myślenia: Zrozumienie zasad dzielenia ułamków ćwiczy logiczne myślenie i rozwiązywanie problemów.
Zrozumienie podstaw: Co to jest ułamek zwykły?
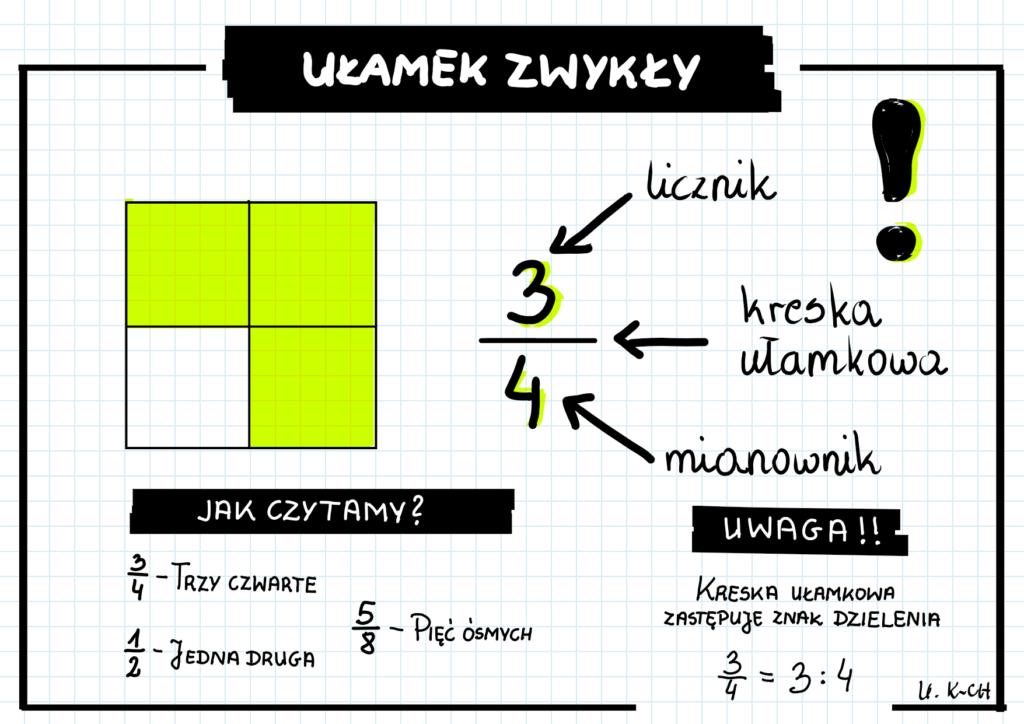
Zanim przejdziemy do dzielenia, przypomnijmy sobie, co to jest ułamek zwykły. Ułamek zwykły reprezentuje część całości. Składa się z dwóch części oddzielonych kreską ułamkową:
- Licznik: Liczba znajdująca się nad kreską ułamkową. Informuje nas, ile części całości posiadamy.
- Mianownik: Liczba znajdująca się pod kreską ułamkową. Informuje nas, na ile równych części podzielona jest całość.
Na przykład, w ułamku 3/4, 3 to licznik, a 4 to mianownik. Oznacza to, że mamy 3 części z 4, na które podzielona jest całość.
Dzielenie ułamków: Krok po kroku
Dzielenie ułamków może wydawać się skomplikowane, ale w rzeczywistości jest to bardzo prosta operacja, gdy zrozumiemy zasadę. Klucz tkwi w odwróceniu drugiego ułamka (dzielnika) i zastąpieniu dzielenia mnożeniem.
Oto kroki, które należy wykonać:
Krok 1: Znajdź odwrotność drugiego ułamka (dzielnika).
Odwrotność ułamka powstaje poprzez zamianę licznika z mianownikiem. Na przykład, odwrotnością ułamka 2/3 jest 3/2.
Przykład: Jeśli dzielimy przez 1/4, jego odwrotność to 4/1 (co jest równe 4).
Krok 2: Zmień operację dzielenia na mnożenie.
Zamiast dzielić przez dany ułamek, będziemy mnożyć przez jego odwrotność.
Przykład: Zamiast 1/2 ÷ 1/4, będziemy liczyć 1/2 × 4/1.
Krok 3: Pomnóż liczniki przez liczniki i mianowniki przez mianowniki.
Aby pomnożyć ułamki, mnożymy liczniki ze sobą, a następnie mianowniki ze sobą.
Przykład: W przypadku 1/2 × 4/1:
- Licznik: 1 × 4 = 4
- Mianownik: 2 × 1 = 2
Otrzymujemy 4/2.
Krok 4: Uprość wynik (jeśli to możliwe).
Wynik, który otrzymaliśmy, często można uprościć. Sprawdzamy, czy licznik i mianownik mają wspólny dzielnik.
Przykład: Ułamek 4/2 można uprościć, dzieląc zarówno licznik, jak i mianownik przez 2. Otrzymujemy 2/1, co jest równe 2.
Przykłady dzielenia ułamków
Spójrzmy na kilka przykładów, aby lepiej zrozumieć ten proces:
Przykład 1: 2/5 ÷ 1/3
- Odwrotność 1/3 to 3/1.
- Zamieniamy dzielenie na mnożenie: 2/5 × 3/1.
- Mnożymy: 2 × 3 = 6 (licznik), 5 × 1 = 5 (mianownik). Otrzymujemy 6/5.
- Ułamek 6/5 jest ułamkiem niewłaściwym (licznik jest większy niż mianownik). Możemy go zamienić na liczbę mieszaną: 1 1/5.
Przykład 2: 3/4 ÷ 1/2
- Odwrotność 1/2 to 2/1.
- Zamieniamy dzielenie na mnożenie: 3/4 × 2/1.
- Mnożymy: 3 × 2 = 6 (licznik), 4 × 1 = 4 (mianownik). Otrzymujemy 6/4.
- Uproszczamy ułamek 6/4, dzieląc licznik i mianownik przez 2. Otrzymujemy 3/2.
- Ułamek 3/2 jest ułamkiem niewłaściwym. Możemy go zamienić na liczbę mieszaną: 1 1/2.
Przykład 3: Dzielenie ułamka przez liczbę całkowitą
Aby podzielić ułamek przez liczbę całkowitą, możemy potraktować liczbę całkowitą jako ułamek z mianownikiem równym 1. Na przykład, 5 to to samo co 5/1.
Załóżmy, że chcemy podzielić 1/3 przez 5.
- Zapisujemy 5 jako ułamek: 5/1.
- Odwrotność 5/1 to 1/5.
- Zamieniamy dzielenie na mnożenie: 1/3 × 1/5.
- Mnożymy: 1 × 1 = 1 (licznik), 3 × 5 = 15 (mianownik). Otrzymujemy 1/15.
Wskazówki i triki
- Pamiętaj o odwracaniu tylko drugiego ułamka (dzielnika). Pierwszy ułamek (dzielna) pozostaje bez zmian.
- Upewnij się, że ułamki są w najprostszej postaci przed rozpoczęciem dzielenia. Uproszczenie ułamków na początku może ułatwić obliczenia.
- Ćwicz regularnie. Im więcej ćwiczysz, tym łatwiej będzie Ci rozwiązywać zadania z dzieleniem ułamków.
- Wykorzystuj wizualizacje. Rysowanie ułamków i ich podział może pomóc w zrozumieniu koncepcji. Możesz użyć kół, prostokątów lub innych kształtów, aby przedstawić ułamki.
Zastosowanie w życiu codziennym
Jak wspomniano na początku, dzielenie ułamków znajduje zastosowanie w wielu sytuacjach życiowych:
- Gotowanie i pieczenie: Dostosowywanie przepisów dla mniejszej lub większej liczby osób.
- Budownictwo i majsterkowanie: Obliczanie proporcji materiałów.
- Finanse: Dzielenie wydatków, obliczanie procentów.
- Podróże: Planowanie trasy, obliczanie czasu podróży, dzielenie kosztów paliwa.
Podsumowanie
Dzielenie ułamków zwykłych to umiejętność, która wydaje się skomplikowana na pierwszy rzut oka, ale w rzeczywistości jest bardzo prosta, jeśli zrozumiemy podstawową zasadę: odwróć drugi ułamek (dzielnik) i pomnóż. Dzięki temu artykułowi mam nadzieję, że proces ten stał się dla Ciebie jaśniejszy i bardziej zrozumiały. Pamiętaj, że praktyka czyni mistrza, więc im więcej ćwiczysz, tym pewniej będziesz się czuł w dzieleniu ułamków. Wykorzystaj tę wiedzę w życiu codziennym i zobacz, jak wiele problemów możesz rozwiązać, wykorzystując tę cenną umiejętność.
Życzę Ci powodzenia w dalszej nauce matematyki! Pamiętaj, że matematyka to nie tylko zbiór wzorów i reguł, ale także narzędzie, które pozwala nam lepiej zrozumieć świat wokół nas.