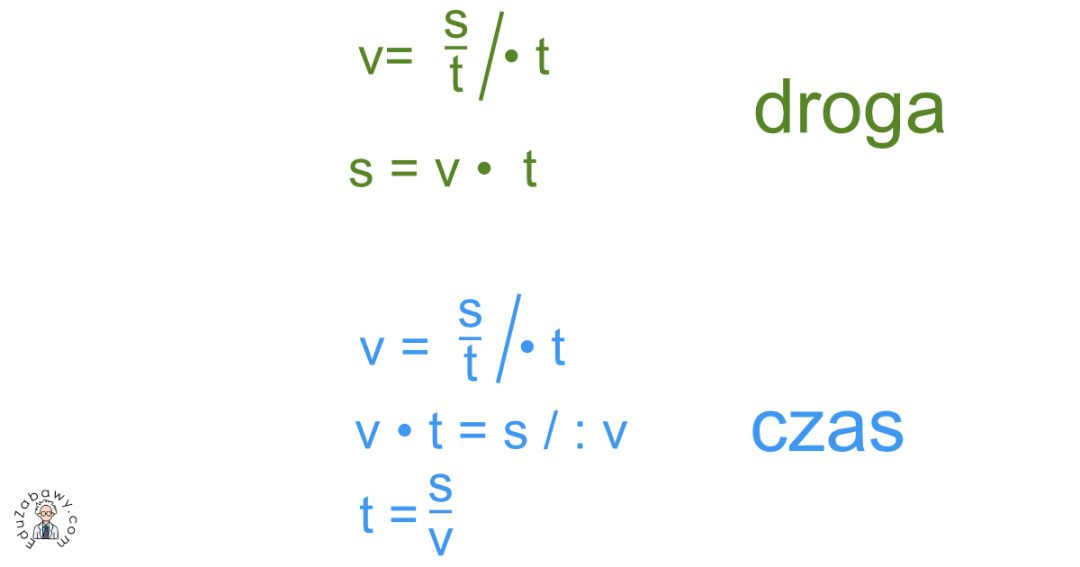Jak Rozwiązywać Zadania Droga Prędkość Czas

Zadania dotyczące drogi, prędkości i czasu są jednymi z podstawowych zagadnień w fizyce i matematyce. Rozumienie relacji między tymi wielkościami jest kluczowe nie tylko w szkole, ale także w życiu codziennym, np. podczas planowania podróży. W tym artykule omówimy, jak rozwiązywać te zadania krok po kroku, prezentując definicje, wzory i przykłady.

Definicje podstawowych pojęć

Zanim przejdziemy do rozwiązywania zadań, warto przypomnieć sobie definicje kluczowych pojęć:

Droga (s): To długość trasy, jaką pokonuje obiekt. Mierzymy ją zazwyczaj w metrach (m) lub kilometrach (km).
Prędkość (v): To szybkość, z jaką obiekt pokonuje drogę. Mierzymy ją najczęściej w metrach na sekundę (m/s) lub kilometrach na godzinę (km/h). Prędkość jest wielkością wektorową, co oznacza, że ma zarówno wartość, jak i kierunek, ale w prostych zadaniach najczęściej rozpatrujemy tylko wartość prędkości.
Czas (t): To okres, w którym obiekt pokonuje daną drogę. Mierzymy go w sekundach (s), minutach (min) lub godzinach (h).

Wzory i relacje

Podstawowa relacja łącząca drogę, prędkość i czas to:

v = s / t

Oznacza to, że prędkość jest równa drodze podzielonej przez czas. Z tego wzoru możemy wyprowadzić dwa kolejne, przydatne w rozwiązywaniu zadań:

s = v * t

Droga jest równa prędkości pomnożonej przez czas.

t = s / v

Czas jest równy drodze podzielonej przez prędkość.

Rozwiązywanie zadań krok po kroku

Oto kilka kroków, które pomogą Ci w rozwiązywaniu zadań dotyczących drogi, prędkości i czasu:

Przeczytaj uważnie treść zadania. Zwróć uwagę na wszystkie podane dane i to, co musisz obliczyć.
Zapisz dane i szukane. To pomoże Ci zorganizować informacje i uniknąć pomyłek.
Wybierz odpowiedni wzór. Zastanów się, który z powyższych wzorów łączy dane, które masz z szukaną wielkością.
Przekształć wzór (jeśli to konieczne). Czasami trzeba przekształcić wzór, aby obliczyć szukaną wielkość.
Podstaw dane do wzoru. Upewnij się, że używasz odpowiednich jednostek! Jeśli masz prędkość w km/h a czas w sekundach, musisz dokonać konwersji jednostek.
Oblicz wynik. Wykonaj obliczenia, używając kalkulatora, jeśli to potrzebne.
Zapisz odpowiedź. Upewnij się, że odpowiedź zawiera odpowiednią jednostkę.

Przykłady zadań

Przykład 1: Obliczanie drogi

Zadanie: Samochód jedzie z prędkością 80 km/h przez 2 godziny. Jaką drogę pokona?

Dane: prędkość (v) = 80 km/h, czas (t) = 2 h
Szukane: droga (s)
Wzór: s = v * t
Obliczenia: s = 80 km/h * 2 h = 160 km
Odpowiedź: Samochód pokona drogę 160 km.

Przykład 2: Obliczanie prędkości

Zadanie: Rowerzysta przejechał 30 km w ciągu 1,5 godziny. Z jaką średnią prędkością jechał?

Dane: droga (s) = 30 km, czas (t) = 1,5 h
Szukane: prędkość (v)
Wzór: v = s / t
Obliczenia: v = 30 km / 1,5 h = 20 km/h
Odpowiedź: Rowerzysta jechał ze średnią prędkością 20 km/h.

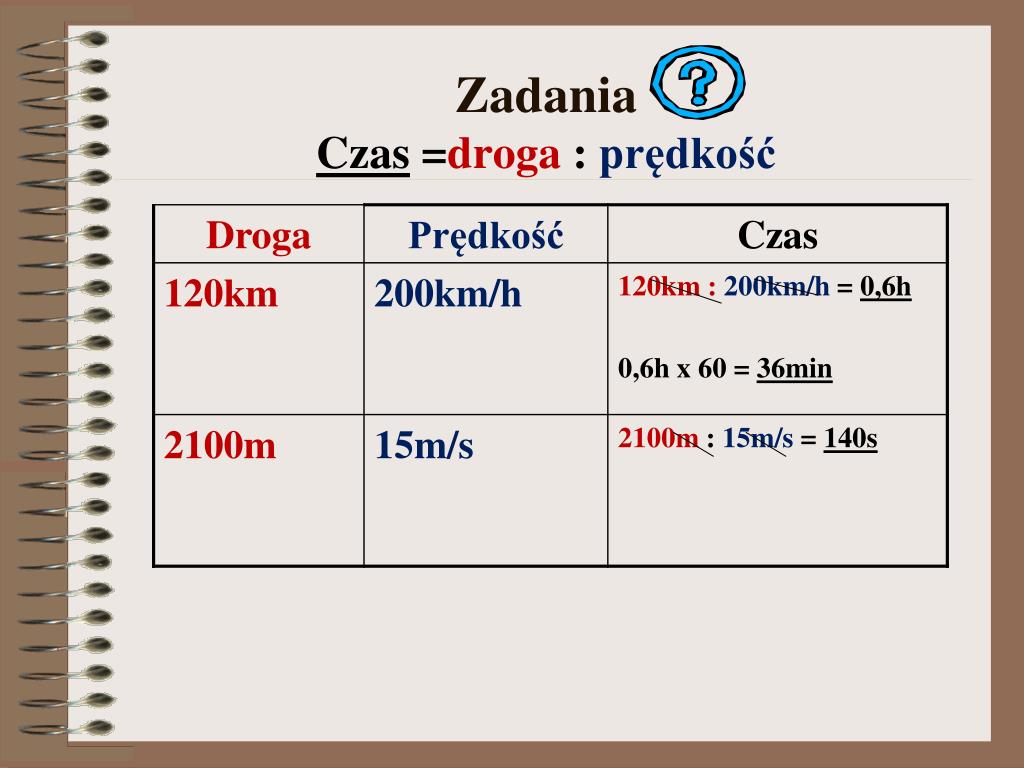
Przykład 3: Obliczanie czasu

Zadanie: Pociąg jedzie z prędkością 120 km/h. Ile czasu zajmie mu pokonanie trasy 360 km?

Dane: prędkość (v) = 120 km/h, droga (s) = 360 km
Szukane: czas (t)
Wzór: t = s / v
Obliczenia: t = 360 km / 120 km/h = 3 h
Odpowiedź: Pociągowi zajmie 3 godziny.

Konwersja jednostek

Często w zadaniach dotyczących drogi, prędkości i czasu musimy dokonywać konwersji jednostek. Oto kilka przykładów:

km/h na m/s: Aby zamienić km/h na m/s, mnożymy wartość w km/h przez 1000/3600 (lub dzielimy przez 3,6). Na przykład: 72 km/h = 72 * (1000/3600) m/s = 20 m/s.
m/s na km/h: Aby zamienić m/s na km/h, mnożymy wartość w m/s przez 3,6. Na przykład: 15 m/s = 15 * 3,6 km/h = 54 km/h.
minuty na godziny: Dzielimy liczbę minut przez 60. Na przykład: 30 minut = 30/60 h = 0,5 h.
sekundy na minuty: Dzielimy liczbę sekund przez 60. Na przykład: 120 sekund = 120/60 min = 2 min.

Zadania złożone

Czasami spotykamy się z zadaniami bardziej złożonymi, w których obiekt porusza się z różnymi prędkościami na różnych odcinkach trasy. W takich przypadkach należy rozbić zadanie na mniejsze etapy, obliczyć drogę, czas lub prędkość dla każdego etapu osobno, a następnie zsumować wyniki.

Na przykład, jeśli samochód jedzie przez 1 godzinę z prędkością 60 km/h, a następnie przez 2 godziny z prędkością 90 km/h, to całkowita droga, jaką pokona, wynosi:

Droga na pierwszym odcinku: s1 = 60 km/h * 1 h = 60 km

Droga na drugim odcinku: s2 = 90 km/h * 2 h = 180 km

Całkowita droga: s = s1 + s2 = 60 km + 180 km = 240 km

Podsumowanie

Rozwiązywanie zadań dotyczących drogi, prędkości i czasu wymaga zrozumienia podstawowych definicji i wzorów. Kluczowe jest uważne czytanie treści zadania, zapisywanie danych i szukanych, wybieranie odpowiedniego wzoru, przekształcanie go w razie potrzeby i dbanie o jednostki. Ćwiczenie i rozwiązywanie różnych przykładów zadań pomoże Ci w opanowaniu tej umiejętności.