Jak Przecinają Się Przekątne W Trapezie Równoramiennym

W trapezie równoramiennym, przekątne przecinają się wewnątrz figury. Co więcej, punkt przecięcia tych przekątnych ma pewne specjalne właściwości. Spróbujmy to sobie wszystko poukładać.

Zacznijmy od przypomnienia sobie, czym w ogóle jest trapez równoramienny. Trapez to czworokąt, który ma jedną parę boków równoległych (nazywamy je podstawami) i jedną parę boków nierównoległych. W trapezie równoramiennym te boki nierównoległe (czyli ramiona) są równej długości. Dodatkowo, w takim trapezie kąty przy każdej z podstaw są równe. Na przykład, kąty przy krótszej podstawie są sobie równe i kąty przy dłuższej podstawie są sobie równe. To bardzo ważne, bo ta symetria trapezu równoramiennego wpływa na to, jak przecinają się jego przekątne.

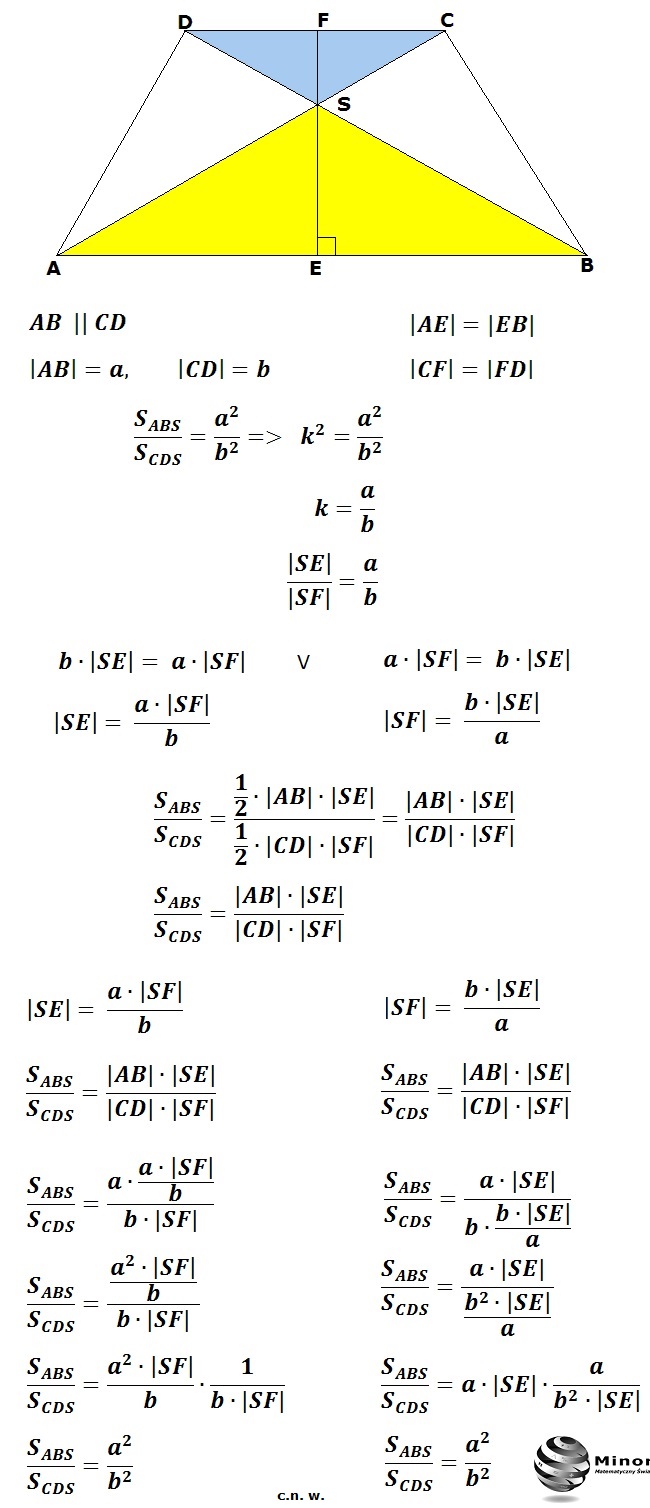
Teraz wyobraź sobie trapez równoramienny ABCD, gdzie AB jest dłuższą podstawą, a CD jest krótszą podstawą. Narysuj przekątne AC i BD. Przecinają się one w punkcie, nazwijmy go punktem O.

Właściwości Punktu Przecięcia Przekątnych

Punkt O, czyli punkt przecięcia przekątnych, dzieli każdą z przekątnych na dwie części. Co ciekawe, te części nie są równe, chyba że trapez jest akurat kwadratem (co jest szczególnym przypadkiem trapezu równoramiennego). W trapezie równoramiennym (który nie jest kwadratem) przekątna jest podzielona na dwa odcinki o różnej długości.

Bardzo ważną rzeczą jest to, że w trapezie równoramiennym przekątne są równej długości. To kolejna konsekwencja symetrii tej figury. Czyli długość odcinka AC jest równa długości odcinka BD.

Punkt O nie jest środkiem żadnej z przekątnych, z wyjątkiem wspomnianego przypadku kwadratu. Oznacza to, że odcinek AO jest dłuższy niż odcinek OC, a odcinek BO jest dłuższy niż odcinek OD. To dlatego, że punkt O jest bliżej dłuższej podstawy trapezu.

Spróbujmy to jeszcze raz. Mamy trapez równoramienny ABCD, przekątne AC i BD przecinają się w punkcie O. Wynika z tego, że:

• Długość AC = Długość BD (przekątne są równe)
• Długość AO ≠ Długość OC (chyba że trapez jest kwadratem)
• Długość BO ≠ Długość OD (chyba że trapez jest kwadratem)
• Długość AO > Długość OC
• Długość BO > Długość OD

Wyobraź sobie teraz trójkąty, które powstają w wyniku przecięcia się przekątnych. Mamy trójkąty AOB, BOC, COD i DOA. Trójkąty AOB i COD są trójkątami równoramiennymi. To kolejna ważna cecha trapezu równoramiennego. Trójkąt AOB ma ramiona AO i BO, a trójkąt COD ma ramiona CO i DO.

Kąty w tych trójkątach też mają swoje własności. Kąty przy podstawie trójkąta AOB są równe, czyli kąt OAB jest równy kątowi OBA. Podobnie, kąty przy podstawie trójkąta COD są równe, czyli kąt OCD jest równy kątowi ODC.

Te wszystkie zależności wynikają z symetrii trapezu równoramiennego. To właśnie ta symetria sprawia, że przekątne przecinają się w sposób, który możemy opisać i zrozumieć.

Jak To Wykorzystać?

Wiedza o tym, jak przecinają się przekątne w trapezie równoramiennym, może być bardzo przydatna przy rozwiązywaniu zadań z geometrii. Na przykład, jeśli znamy długość jednej z przekątnych i wiemy, w jakim stosunku punkt przecięcia dzieli tę przekątną, możemy obliczyć długości odcinków, na które została ona podzielona.

Możemy też wykorzystać tę wiedzę do obliczania pól trójkątów, które powstają w wyniku przecięcia się przekątnych. Znając długości podstaw i wysokości tych trójkątów (które często można wyliczyć, korzystając z własności trapezu równoramiennego), możemy bez problemu obliczyć ich pola.

Pamiętaj, że trapez równoramienny ma wiele specyficznych cech, które ułatwiają rozwiązywanie zadań. Warto zapamiętać te cechy i umieć je wykorzystać. Równość ramion, równość kątów przy podstawach, równość przekątnych – to wszystko bardzo przydatne informacje. Dodatkowo, wiedza o tym, jak przecinają się przekątne i jakie trójkąty powstają w wyniku tego przecięcia, może znacznie ułatwić nam pracę.

Podsumowując, punkt przecięcia przekątnych w trapezie równoramiennym jest ważnym punktem, który dzieli przekątne na odcinki o różnej długości (z wyjątkiem przypadku kwadratu). Przekątne są równe, a trójkąty AOB i COD (gdzie O to punkt przecięcia) są równoramienne. Ta wiedza może być bardzo przydatna w rozwiązywaniu zadań geometrycznych związanych z trapezami równoramiennymi. Im więcej wiesz o własnościach figur geometrycznych, tym łatwiej jest Ci rozwiązywać zadania i rozumieć geometrię.

Pamiętaj o rysunku pomocniczym! Zawsze, gdy masz do czynienia z zadaniem geometrycznym, narysuj sobie schematyczny rysunek. Zaznacz na nim wszystkie dane, które znasz, i oznacz to, co masz obliczyć. Rysunek bardzo często pomaga zrozumieć zadanie i znaleźć sposób na jego rozwiązanie. W przypadku trapezu równoramiennego, rysunek powinien uwzględniać równość ramion, równość kątów przy podstawach oraz przecinające się przekątne. Zaznacz punkt przecięcia przekątnych i spróbuj dostrzec trójkąty, które powstają. Często to właśnie analiza tych trójkątów prowadzi do rozwiązania zadania.