Jak Obliczyc Wysokosc W Ostroslupie

Obliczanie wysokości w ostrosłupie jest kluczowe do określenia jego objętości i pola powierzchni. Choć na pierwszy rzut oka może się to wydawać skomplikowane, zrozumienie podstawowych zasad geometrii i zastosowanie odpowiednich wzorów pozwala na rozwiązanie większości problemów. W tym artykule omówimy różne metody obliczania wysokości ostrosłupa, w zależności od dostępnych danych i rodzaju ostrosłupa.

Podstawy Ostrosłupa

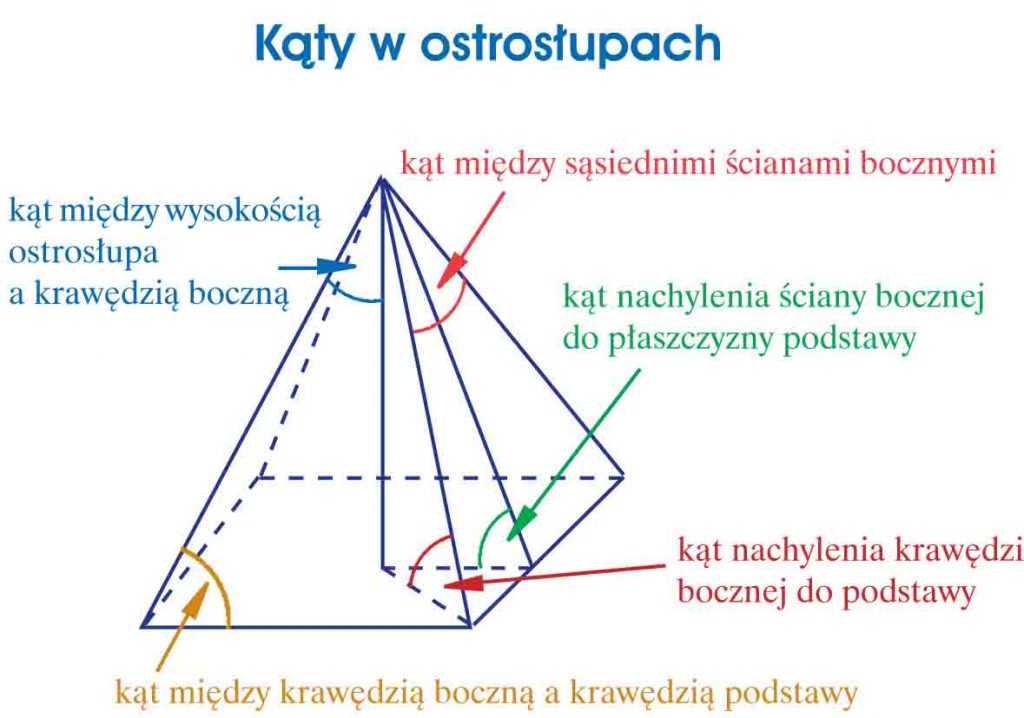
Zanim przejdziemy do obliczeń, warto przypomnieć sobie definicję i charakterystyczne cechy ostrosłupa. Ostrosłup to wielościan, którego podstawą jest wielokąt, a ściany boczne są trójkątami zbiegającymi się w jednym punkcie zwanym wierzchołkiem ostrosłupa. Wysokość ostrosłupa to odcinek prostopadły poprowadzony z wierzchołka ostrosłupa do płaszczyzny podstawy. Niezwykle ważne jest, aby zrozumieć, że wysokość nie zawsze leży wewnątrz ostrosłupa; może znajdować się poza nim, szczególnie w przypadku ostrosłupów pochyłych.

Rodzaje Ostrosłupów

Istnieje kilka rodzajów ostrosłupów, które wpływają na sposób obliczania ich wysokości:

• Ostrosłup prosty: Jego podstawa jest wielokątem foremnym, a wysokość opada prostopadle na środek podstawy.
• Ostrosłup prawidłowy: Jest to ostrosłup prosty, którego wszystkie krawędzie boczne są równe.
• Ostrosłup pochyły: Jego wysokość nie opada na środek podstawy. Obliczenia w tym przypadku są bardziej skomplikowane.
• Ostrosłup foremny: Podstawa jest wielokątem foremnym, ale niekoniecznie wysokość musi padać na jego środek.

Metody Obliczania Wysokości w Ostrosłupie Prostym

Obliczanie wysokości w ostrosłupie prostym jest zazwyczaj najprostsze, ponieważ możemy wykorzystać twierdzenie Pitagorasa.

Wykorzystanie Twierdzenia Pitagorasa

Jeżeli znamy długość krawędzi bocznej (l) ostrosłupa i odległość (r) od środka podstawy do wierzchołka podstawy (np. połowa długości boku w podstawie kwadratowej), to możemy obliczyć wysokość (h) korzystając z twierdzenia Pitagorasa:

h² + r² = l²

Stąd: h = √(l² - r²)

Przykład: Mamy ostrosłup prosty o podstawie kwadratowej. Długość krawędzi bocznej wynosi 10 cm, a długość boku podstawy wynosi 8 cm. Oblicz wysokość ostrosłupa.

Rozwiązanie:

1. Obliczamy odległość r od środka podstawy do wierzchołka podstawy. W kwadracie jest to połowa długości przekątnej. Przekątna kwadratu o boku a wynosi a√2, więc r = (a√2)/2 = (8√2)/2 = 4√2 cm.
2. Podstawiamy wartości do wzoru: h = √(10² - (4√2)²) = √(100 - 32) = √68 ≈ 8.25 cm.

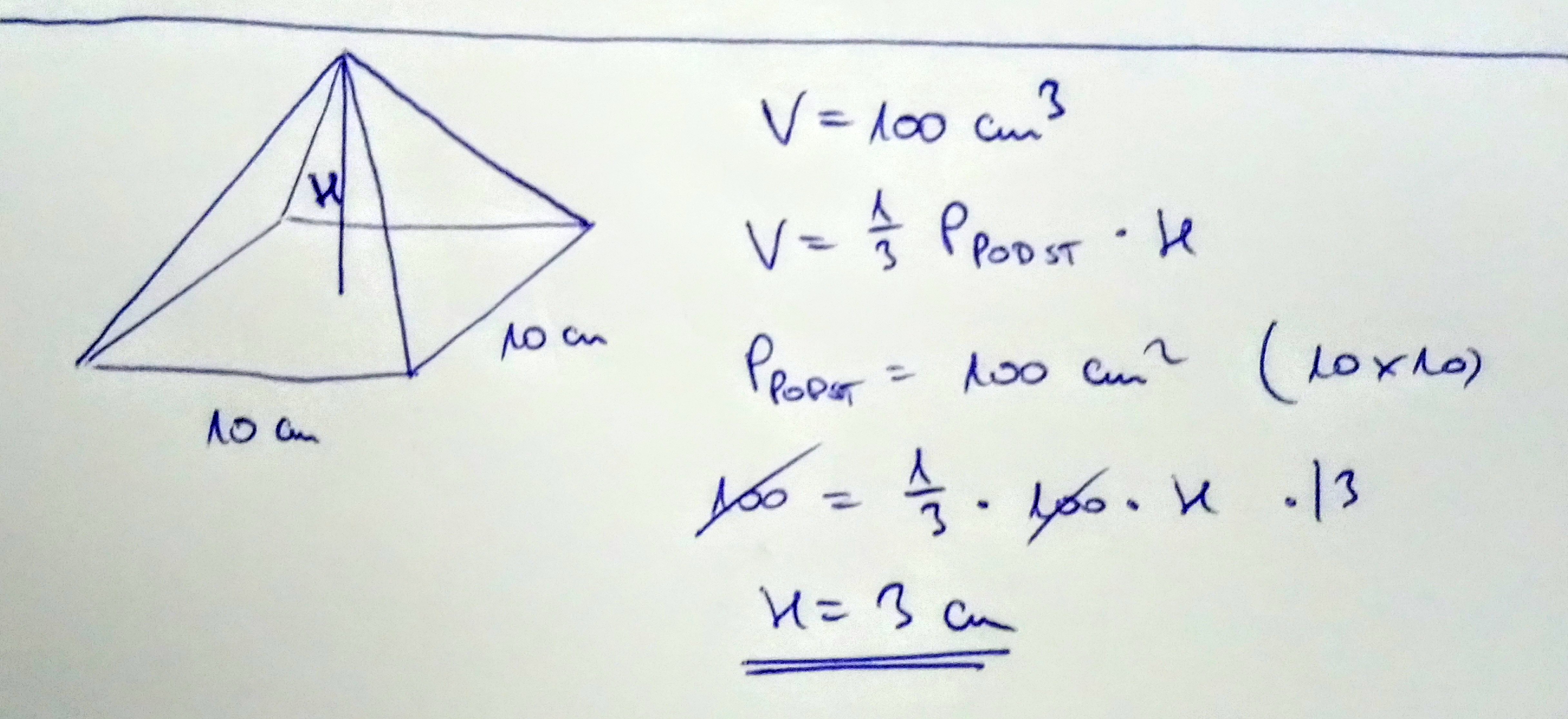
Znając Objętość i Pole Podstawy

Jeżeli znamy objętość (V) ostrosłupa i pole jego podstawy (P_p), to możemy obliczyć wysokość (h) korzystając z wzoru na objętość ostrosłupa:

V = (1/3) * P_p * h

Stąd: h = (3 * V) / P_p

Przykład: Objętość ostrosłupa wynosi 60 cm³, a pole jego podstawy wynosi 20 cm². Oblicz wysokość ostrosłupa.

Rozwiązanie:

1. Podstawiamy wartości do wzoru: h = (3 * 60) / 20 = 180 / 20 = 9 cm.

Obliczanie Wysokości w Ostrosłupie Pochyłym

Obliczanie wysokości w ostrosłupie pochyłym jest bardziej skomplikowane, ponieważ wysokość nie pada na środek podstawy. Wymaga to zazwyczaj więcej informacji o geometrii ostrosłupa, np. o kątach nachylenia ścian bocznych do podstawy lub o położeniu punktu, w którym wysokość przecina płaszczyznę podstawy.

Wykorzystanie Trygonometrii

Jeżeli znamy kąt (α) nachylenia krawędzi bocznej do płaszczyzny podstawy i długość tej krawędzi (l), oraz położenie punktu przecięcia wysokości z podstawą, możemy wykorzystać funkcje trygonometryczne do obliczenia wysokości. Załóżmy, że odległość od punktu, w którym wysokość przecina podstawę, do wierzchołka podstawy, który jest końcem krawędzi bocznej, wynosi d.

Wtedy: h = l * sin(α) lub jeżeli znamy d, a nie l, możemy użyć tangensa: h = d * tan(α), jeśli znamy kąt nachylenia ściany bocznej do podstawy.

Przykład: Krawędź boczna ostrosłupa pochyłego ma długość 12 cm i nachylona jest do podstawy pod kątem 60 stopni. Oblicz wysokość ostrosłupa.

Rozwiązanie:

1. Podstawiamy wartości do wzoru: h = 12 * sin(60°) = 12 * (√3 / 2) = 6√3 ≈ 10.39 cm.

Metody Analityczne

W bardziej skomplikowanych przypadkach, szczególnie gdy mamy do czynienia z ostrosłupem o nieregularnej podstawie, możemy skorzystać z metod analitycznych. Oznacza to, że definiujemy współrzędne wierzchołków ostrosłupa w przestrzeni trójwymiarowej i wykorzystujemy wektory do obliczenia odległości wierzchołka od płaszczyzny podstawy. W tym przypadku należy:

1. Wyznaczyć równanie płaszczyzny podstawy.
2. Obliczyć odległość wierzchołka od tej płaszczyzny.

Odległość punktu (x₀, y₀, z₀) od płaszczyzny opisanej równaniem Ax + By + Cz + D = 0 wyraża się wzorem:

d = |Ax₀ + By₀ + Cz₀ + D| / √(A² + B² + C²)

Ta odległość jest właśnie wysokością ostrosłupa.

Real-World Examples

Obliczanie wysokości ostrosłupa znajduje zastosowanie w wielu dziedzinach, takich jak:

• Architektura: Projektowanie dachów w kształcie ostrosłupów, piramid, gdzie znajomość wysokości jest niezbędna do obliczenia objętości przestrzeni i ilości potrzebnych materiałów.
• Inżynieria: Obliczanie objętości nasypów, pryzm, kopców o kształcie zbliżonym do ostrosłupów.
• Geometria: Rozwiązywanie problemów matematycznych i zadań związanych z ostrosłupami.
• Kartografia: Modelowanie terenu, gdzie góry i wzniesienia mogą być przybliżane do ostrosłupów.
• Projektowanie opakowań: Tworzenie opakowań w kształcie ostrosłupów, wymagające precyzyjnych obliczeń wymiarów.

Przykładowo, projektując piramidalny dach budynku, architekt musi precyzyjnie obliczyć wysokość ostrosłupa, aby oszacować ilość materiału potrzebnego do pokrycia dachu i obliczyć obciążenie konstrukcji.

Zakończenie

Obliczanie wysokości w ostrosłupie wymaga zrozumienia jego geometrii i zastosowania odpowiednich wzorów. Wybór metody zależy od dostępnych danych i rodzaju ostrosłupa. Pamiętaj, że w przypadku ostrosłupów pochyłych obliczenia są bardziej skomplikowane i mogą wymagać wykorzystania trygonometrii lub metod analitycznych. Ćwiczenie rozwiązywania różnych zadań pomoże Ci utrwalić wiedzę i nabyć umiejętność efektywnego obliczania wysokości w ostrosłupach.

Zachęcam do dalszego zgłębiania wiedzy z zakresu geometrii i eksplorowania zastosowań ostrosłupów w różnych dziedzinach. Sprawdź dostępne zasoby online, podręczniki i ćwiczenia, aby doskonalić swoje umiejętności.