Jak Obliczyć Współczynnik Kierunkowy Mając Dwa Punkty

Hej klaso! Widzę, że macie pytania dotyczące obliczania współczynnika kierunkowego, mając dwa punkty. To świetnie, że jesteście ciekawi! Spróbuję wytłumaczyć to w prosty sposób.

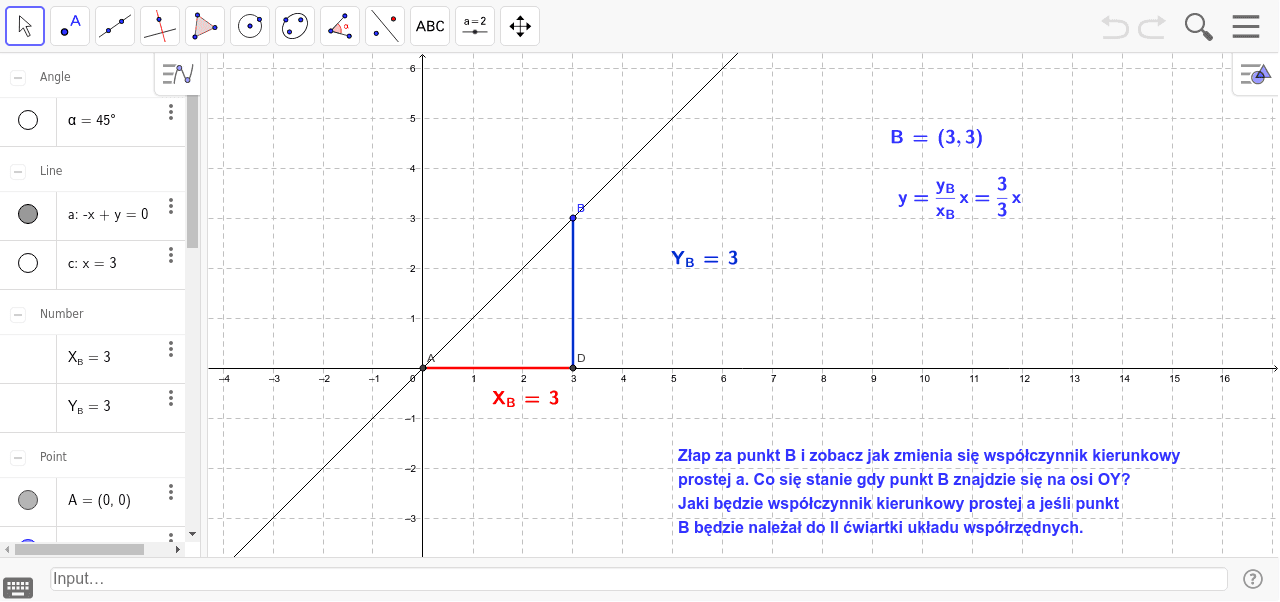
Żeby obliczyć współczynnik kierunkowy prostej, potrzebujemy dwóch punktów, które na tej prostej leżą. Nazwijmy je A i B. Każdy punkt ma swoje współrzędne: x i y. Zatem punkt A ma współrzędne (x_A, y_A), a punkt B ma współrzędne (x_B, y_B).

Współczynnik kierunkowy, który często oznaczamy literą "a", mówi nam, jak bardzo stroma jest nasza prosta. Mówi nam, o ile wzrasta (lub maleje) wartość y, kiedy wartość x wzrasta o jeden.

Mamy wzór, który pomoże nam to obliczyć:

a = (y_B - y_A) / (x_B - x_A)

Czyli, od współrzędnej y punktu B odejmujemy współrzędną y punktu A. Potem, od współrzędnej x punktu B odejmujemy współrzędną x punktu A. Na koniec dzielimy wynik odejmowania y przez wynik odejmowania x.

Przykład

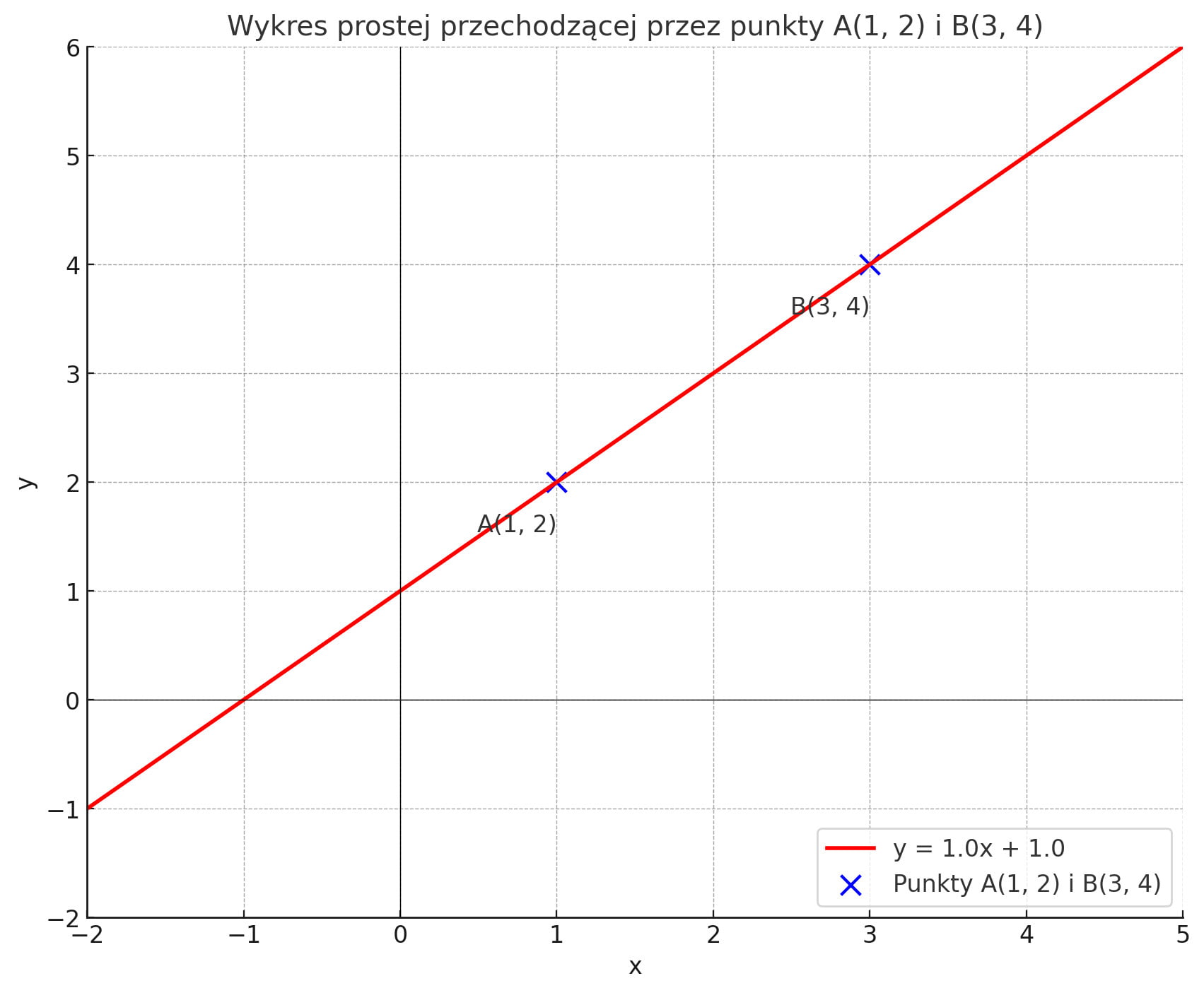
Załóżmy, że mamy punkt A o współrzędnych (1, 2) i punkt B o współrzędnych (3, 6).

1. Odejmujemy y: 6 - 2 = 4
2. Odejmujemy x: 3 - 1 = 2
3. Dzielimy wyniki: 4 / 2 = 2

Współczynnik kierunkowy tej prostej wynosi 2. Oznacza to, że idąc po tej prostej, kiedy x wzrasta o 1, y wzrasta o 2.

Co robić, gdy x_B - x_A = 0?

Jeśli zdarzy się, że po odjęciu x_B od x_A otrzymamy zero, oznacza to, że prosta jest pionowa. W takim przypadku współczynnik kierunkowy nie istnieje (mówimy, że jest nieokreślony). Dzieje się tak, ponieważ nie możemy dzielić przez zero. Proste pionowe mają równanie x = stała, gdzie stała to wartość x punktu na prostej.

Kilka Dodatkowych Przykładów

Żeby lepiej to zrozumieć, rozwiążmy jeszcze kilka przykładów.

Przykład 2:

Punkt A = (-2, 1) Punkt B = (4, 7)

1. Odejmujemy y: 7 - 1 = 6
2. Odejmujemy x: 4 - (-2) = 4 + 2 = 6
3. Dzielimy wyniki: 6 / 6 = 1

Współczynnik kierunkowy tej prostej wynosi 1.

Przykład 3:

Punkt A = (0, -3) Punkt B = (5, 2)

1. Odejmujemy y: 2 - (-3) = 2 + 3 = 5
2. Odejmujemy x: 5 - 0 = 5
3. Dzielimy wyniki: 5 / 5 = 1

Współczynnik kierunkowy tej prostej wynosi 1.

Przykład 4:

Punkt A = (-1, 4) Punkt B = (2, -2)

1. Odejmujemy y: -2 - 4 = -6
2. Odejmujemy x: 2 - (-1) = 2 + 1 = 3
3. Dzielimy wyniki: -6 / 3 = -2

Współczynnik kierunkowy tej prostej wynosi -2. Zwróćcie uwagę na znak minus. Oznacza on, że prosta opada, czyli kiedy x wzrasta, y maleje.

Przykład 5 (Prosta pionowa):

Punkt A = (3, 1) Punkt B = (3, 5)

1. Odejmujemy y: 5 - 1 = 4
2. Odejmujemy x: 3 - 3 = 0

Ponieważ otrzymaliśmy zero w mianowniku, współczynnik kierunkowy nie istnieje. To prosta pionowa o równaniu x = 3.

Pamiętajcie, żeby zawsze podstawiać współrzędne do wzoru w odpowiedniej kolejności. Ważne jest, żeby odejmować y_A od y_B i x_A od x_B. Jeśli pomylimy kolejność, otrzymamy wynik o przeciwnym znaku, co zmieni kierunek prostej.

Mam nadzieję, że teraz rozumiecie, jak obliczyć współczynnik kierunkowy prostej, mając dwa punkty. Ćwiczcie na różnych przykładach, a szybko nabierzecie wprawy! Powodzenia!