Jak Obliczyc Pole Trojkata Rownoramiennego Bez Wysokosci

Aby obliczyć pole trójkąta równoramiennego bez konieczności znajdowania jego wysokości, istnieje kilka alternatywnych metod, które wykorzystują inne znane parametry trójkąta. Przyjrzyjmy się niektórym z nich.

Jeżeli znamy długości wszystkich boków trójkąta równoramiennego, możemy skorzystać ze wzoru Herona. Wzór ten pozwala na obliczenie pola dowolnego trójkąta, znając jedynie długości jego boków. W przypadku trójkąta równoramiennego, gdzie dwa boki są równe (oznaczmy je jako 'a'), a trzeci bok (podstawa) ma długość 'b', wzór Herona przyjmuje nieco prostszą formę.

Najpierw obliczamy połowę obwodu trójkąta, którą oznaczamy jako 'p':

p = (a + a + b) / 2 = (2a + b) / 2

Następnie, pole trójkąta (P) obliczamy według wzoru:

P = √(p * (p - a) * (p - a) * (p - b)) = √(p * (p - a)² * (p - b))

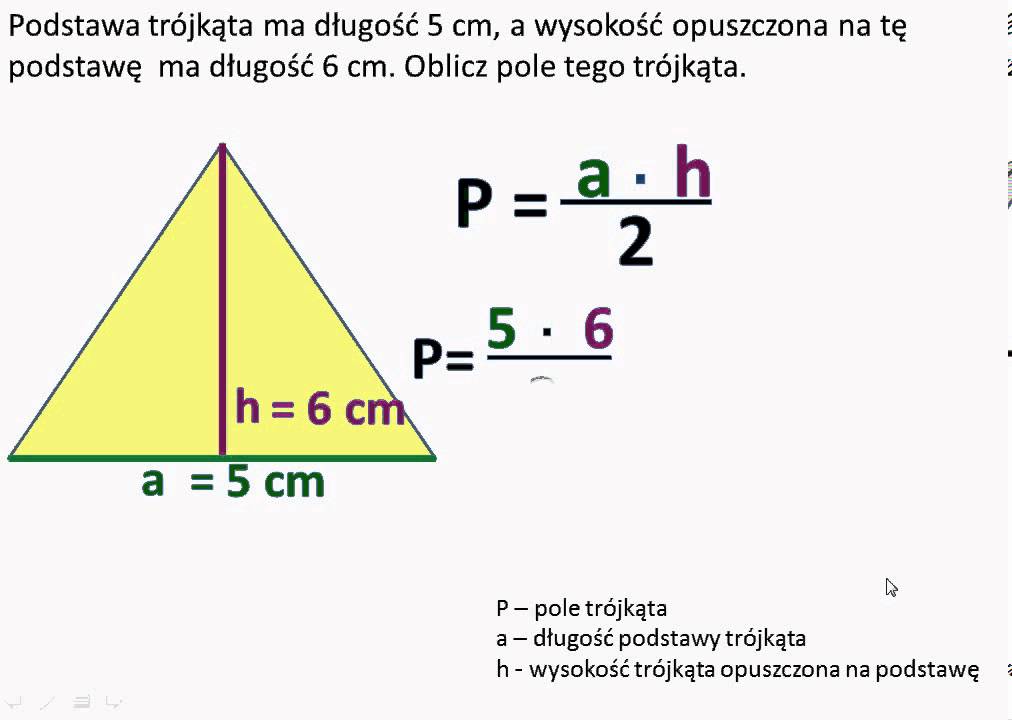
Zastosujmy to na przykładzie. Załóżmy, że mamy trójkąt równoramienny o bokach długości a = 5 cm i podstawie b = 6 cm.

Obliczamy połowę obwodu:

p = (2 * 5 + 6) / 2 = (10 + 6) / 2 = 16 / 2 = 8 cm

Teraz obliczamy pole:

P = √(8 * (8 - 5)² * (8 - 6)) = √(8 * 3² * 2) = √(8 * 9 * 2) = √144 = 12 cm²

Zatem, pole tego trójkąta równoramiennego wynosi 12 cm².

Jeżeli znamy długość jednego z ramion (a) i kąt między ramionami (γ), możemy obliczyć pole trójkąta za pomocą wzoru:

P = (1/2) * a² * sin(γ)

Wyjaśnijmy to na przykładzie. Mamy trójkąt równoramienny, gdzie ramię ma długość a = 7 cm, a kąt między ramionami wynosi γ = 60°.

Pole obliczamy następująco:

P = (1/2) * 7² * sin(60°) = (1/2) * 49 * (√3 / 2) = (49√3) / 4 cm²

Przybliżona wartość pola to:

P ≈ (49 * 1.732) / 4 ≈ 21.18 cm²

Więc pole tego trójkąta równoramiennego wynosi około 21.18 cm².

Jeśli znamy długość podstawy (b) i kąt między podstawą a ramieniem (α), możemy skorzystać z zależności trygonometrycznych, aby wyrazić długość ramienia (a) w zależności od długości podstawy i kąta, a następnie obliczyć pole.

Zauważmy, że wysokość trójkąta równoramiennego opuszczona na podstawę dzieli podstawę na dwie równe części. Oznacza to, że możemy utworzyć trójkąt prostokątny, którego przeciwprostokątną jest ramię trójkąta równoramiennego (a), przyprostokątną przyległą do kąta α jest połowa podstawy (b/2), a przyprostokątną naprzeciwległą jest wysokość (h).

Z definicji cosinusa mamy:

cos(α) = (b/2) / a

Stąd, możemy wyrazić długość ramienia (a) jako:

a = (b/2) / cos(α)

Teraz, aby obliczyć pole, potrzebujemy wysokości (h). Z definicji sinusa mamy:

sin(α) = h / a

Stąd:

h = a * sin(α)

Podstawiając wyrażenie na 'a', otrzymujemy:

h = ((b/2) / cos(α)) * sin(α) = (b/2) * tan(α)

Teraz, mając długość podstawy (b) i wysokość (h), możemy obliczyć pole trójkąta:

P = (1/2) * b * h = (1/2) * b * (b/2) * tan(α) = (b² * tan(α)) / 4

Rozważmy przykład. Załóżmy, że mamy trójkąt równoramienny o podstawie b = 8 cm i kącie między podstawą a ramieniem α = 45°.

Pole obliczamy:

P = (8² * tan(45°)) / 4 = (64 * 1) / 4 = 16 cm²

Więc pole tego trójkąta równoramiennego wynosi 16 cm².

Wykorzystanie Twierdzenia Pitagorasa po Wyznaczeniu Połowy Podstawy

Jeżeli dysponujemy długością ramienia (a) i podstawy (b) trójkąta równoramiennego, możemy obliczyć wysokość (h) opuszczoną na podstawę, korzystając z twierdzenia Pitagorasa. Jak wcześniej wspomniano, wysokość ta dzieli podstawę na dwie równe części, tworząc dwa trójkąty prostokątne.

W każdym z tych trójkątów prostokątnych:

• Przeciwprostokątna to ramię trójkąta równoramiennego (a).
• Jedna z przyprostokątnych to połowa podstawy (b/2).
• Druga przyprostokątna to wysokość (h).

Z twierdzenia Pitagorasa wynika:

a² = (b/2)² + h²

Przekształcając to równanie, aby wyznaczyć wysokość (h), otrzymujemy:

h² = a² - (b/2)²

h = √(a² - (b/2)²)

Po obliczeniu wysokości (h), pole trójkąta równoramiennego możemy obliczyć ze wzoru:

P = (1/2) * b * h = (1/2) * b * √(a² - (b/2)²)

Przyjrzyjmy się przykładowi. Załóżmy, że mamy trójkąt równoramienny o ramieniu a = 10 cm i podstawie b = 12 cm.

Obliczamy wysokość:

h = √(10² - (12/2)²) = √(100 - 6²) = √(100 - 36) = √64 = 8 cm

Następnie obliczamy pole:

P = (1/2) * 12 * 8 = 6 * 8 = 48 cm²

Zatem, pole tego trójkąta równoramiennego wynosi 48 cm².

Zastosowanie Geometrii Analitycznej

W przypadku, gdy trójkąt równoramienny jest umieszczony w układzie współrzędnych i znamy współrzędne jego wierzchołków, możemy obliczyć pole, korzystając ze wzoru na pole trójkąta o znanych współrzędnych wierzchołków. Załóżmy, że współrzędne wierzchołków trójkąta to A(x1, y1), B(x2, y2) i C(x3, y3). Wówczas pole trójkąta (P) można obliczyć za pomocą następującego wzoru:

P = (1/2) * |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|

Wartość bezwzględna jest konieczna, ponieważ pole musi być wartością dodatnią. Ważne jest, aby punkty A, B i C były podane w kolejności przeciwniej do ruchu wskazówek zegara (lub zgodnie z ruchem wskazówek zegara, ale konsekwentnie), aby uzyskać dodatnią wartość determinantu przed zastosowaniem wartości bezwzględnej. Jeśli kolejność jest odwrotna, wynik będzie ujemny, ale wartość bezwzględna zapewni prawidłowe pole.

Rozważmy przykład. Załóżmy, że wierzchołki trójkąta równoramiennego mają współrzędne A(1, 2), B(5, 2) i C(3, 5).

Obliczamy pole:

P = (1/2) * |1(2 - 5) + 5(5 - 2) + 3(2 - 2)| = (1/2) * |1(-3) + 5(3) + 3(0)| = (1/2) * |-3 + 15 + 0| = (1/2) * |12| = (1/2) * 12 = 6

Zatem, pole tego trójkąta równoramiennego wynosi 6 jednostek kwadratowych. Podsumowując, istnieje wiele sposobów na obliczenie pola trójkąta równoramiennego bez konieczności znajdowania wysokości. Wybór metody zależy od dostępnych danych. Wzór Herona jest uniwersalny, jeśli znamy długości wszystkich boków. Jeżeli znamy ramię i kąt między ramionami, możemy skorzystać ze wzoru z sinusem. Znając podstawę i kąt między podstawą a ramieniem, możemy wykorzystać zależności trygonometryczne. A jeżeli znamy współrzędne wierzchołków w układzie współrzędnych, pomocna będzie geometria analityczna. Każda z tych metod pozwala na efektywne obliczenie pola, unikając obliczania wysokości.