Jak Obliczyć Pole Kwadratu Z Przekątnej

Czy kiedykolwiek stanęliście przed problemem obliczenia pola kwadratu, mając daną jedynie długość jego przekątnej? To zadanie, które na pierwszy rzut oka może wydawać się skomplikowane, ale w rzeczywistości jest zaskakująco proste, gdy zrozumiemy podstawowe zasady geometrii. Ten artykuł jest skierowany do uczniów, studentów, hobbystów matematycznych oraz każdego, kto pragnie odświeżyć swoją wiedzę z zakresu geometrii i nauczyć się szybkiego sposobu na obliczenie pola kwadratu z przekątnej.

Wprowadzenie do kwadratu i jego własności

Zanim przejdziemy do konkretnych obliczeń, przypomnijmy sobie, czym tak naprawdę jest kwadrat. Kwadrat to czworokąt foremny, co oznacza, że wszystkie jego boki są równe, a wszystkie kąty wewnętrzne są proste (90 stopni). Te dwie cechy sprawiają, że kwadrat jest szczególnym przypadkiem prostokąta oraz rombu. Co więcej, kwadrat posiada dwie przekątne, które przecinają się pod kątem prostym w swoim środku, dzieląc kwadrat na cztery identyczne trójkąty prostokątne równoramienne.

Podstawowe własności kwadratu:

• Wszystkie boki są równe.
• Wszystkie kąty wewnętrzne są proste (90°).
• Przekątne są równe i przecinają się pod kątem prostym w swoim środku.
• Przekątne dzielą kąty kwadratu na połowy (45°).

Związek między bokiem a przekątną kwadratu

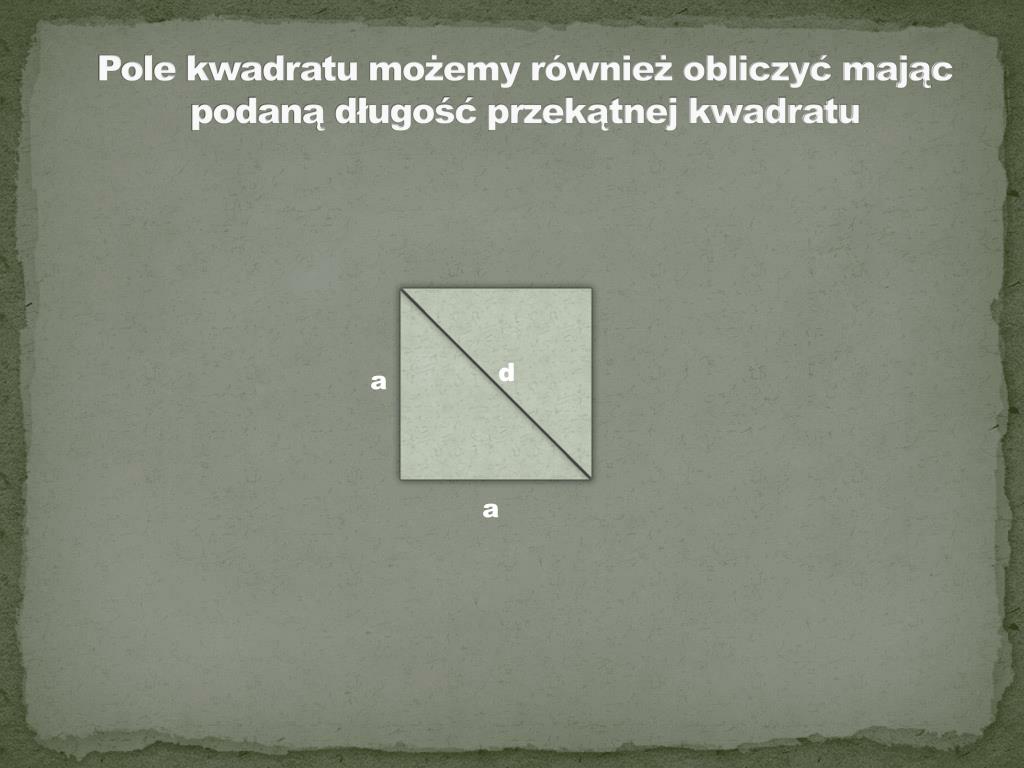
Kluczem do obliczenia pola kwadratu z przekątnej jest zrozumienie związku między długością boku kwadratu (oznaczmy go jako a) a długością jego przekątnej (oznaczmy ją jako d). Ten związek wynika bezpośrednio z twierdzenia Pitagorasa. Spójrzmy na jeden z trójkątów prostokątnych, na które przekątna dzieli kwadrat. Jego przyprostokątnymi są boki kwadratu (oba o długości a), a przeciwprostokątną jest przekątna (o długości d).

Zgodnie z twierdzeniem Pitagorasa:

a² + a² = d²

Upraszczając to równanie, otrzymujemy:

2a² = d²

Stąd możemy wyznaczyć długość boku kwadratu:

a = √(d² / 2) = (d / √2)

Warto zapamiętać ten wzór, ponieważ będzie on pomocny w dalszych obliczeniach. Jednak, jak zaraz zobaczymy, możemy obejść się bez bezpośredniego wyznaczania długości boku.

Wzór na pole kwadratu

Pole kwadratu, oznaczane zazwyczaj jako P, obliczamy, mnożąc długość boku przez samą siebie:

P = a²

To podstawowy wzór, który prawdopodobnie wszyscy pamiętają ze szkoły. Teraz spróbujemy wyrazić pole kwadratu bezpośrednio za pomocą długości przekątnej.

Obliczanie pola kwadratu z przekątnej - krok po kroku

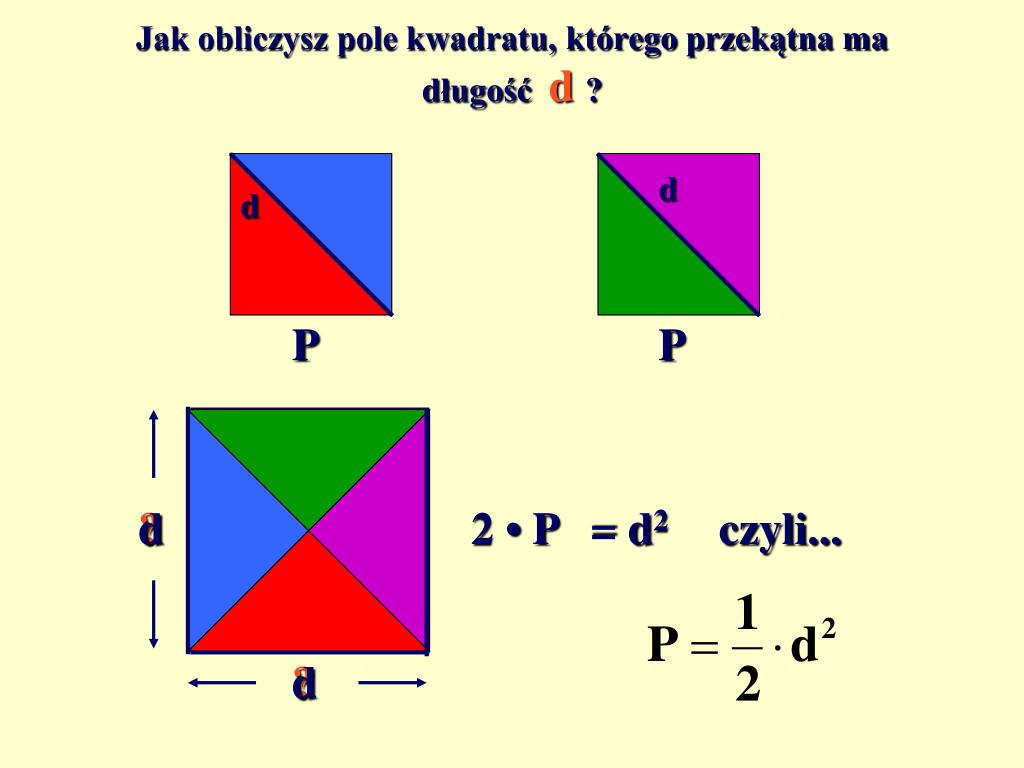
Mając już wzór na pole kwadratu (P = a²) oraz związek między bokiem a przekątną (2a² = d²), możemy wyprowadzić wzór na pole kwadratu wyrażone za pomocą przekątnej.

Wiemy, że 2a² = d². Podzielmy obie strony równania przez 2:

a² = d² / 2

Ponieważ P = a², możemy bezpośrednio podstawić:

P = d² / 2

Oto kluczowy wzór: Pole kwadratu jest równe kwadratowi długości jego przekątnej podzielonemu przez 2.

To bardzo proste i eleganckie rozwiązanie. Nie musimy obliczać długości boku, aby znaleźć pole kwadratu, znając jedynie jego przekątną!

Przykład obliczeniowy

Załóżmy, że mamy kwadrat, którego przekątna ma długość 6 cm. Jak obliczyć jego pole?

Zastosujmy wzór: P = d² / 2

P = (6 cm)² / 2

P = 36 cm² / 2

P = 18 cm²

Zatem pole kwadratu o przekątnej długości 6 cm wynosi 18 cm².

Zastosowania praktyczne

Gdzie możemy wykorzystać tę wiedzę w życiu codziennym? Oto kilka przykładów:

• Projektowanie wnętrz: Wyobraź sobie, że planujesz ułożyć parkiet z kwadratowych płytek, a masz jedynie informację o długości przekątnej pomieszczenia. Możesz szybko obliczyć powierzchnię, którą musisz pokryć.
• Budownictwo: Podczas planowania ogrodu lub tarasu, możesz potrzebować obliczyć powierzchnię kwadratowych elementów, mając dane o ich przekątnych.
• Zadania matematyczne: Oczywiście, ta wiedza jest niezbędna podczas rozwiązywania zadań z geometrii w szkole lub na studiach.

Podsumowanie i zapamiętanie wzoru

Nauczyliśmy się, jak obliczyć pole kwadratu, mając daną długość jego przekątnej. Kluczowy wzór to:

P = d² / 2

Gdzie:

• P to pole kwadratu.
• d to długość przekątnej kwadratu.

Zapamiętaj ten wzór, a obliczanie pola kwadratu z przekątnej stanie się dla Ciebie dziecinnie proste. Możesz go łatwo wyprowadzić, pamiętając o twierdzeniu Pitagorasa i związku między bokiem a przekątną kwadratu. Ćwicz regularnie, rozwiązując różne zadania, a szybko nabierzesz wprawy.

Dlaczego warto znać ten sposób?

Znajomość tego wzoru to świetny sposób na zaoszczędzenie czasu podczas rozwiązywania problemów geometrycznych. Zamiast obliczać długość boku, a następnie pole, możesz bezpośrednio obliczyć pole, znając jedynie długość przekątnej. To szczególnie przydatne w sytuacjach, gdy czas jest ograniczony, na przykład podczas egzaminów lub testów.

Co więcej, zrozumienie tego związku pogłębia Twoje zrozumienie geometrii i relacji między różnymi elementami kwadratu. To nie tylko zapamiętanie wzoru, ale przede wszystkim zrozumienie, skąd się on bierze i dlaczego działa. Takie podejście sprawia, że matematyka staje się bardziej intuicyjna i przyjemna.

Mam nadzieję, że ten artykuł pomógł Wam zrozumieć, jak obliczyć pole kwadratu z przekątnej. Teraz możecie z powodzeniem zmierzyć się z zadaniami, które wcześniej wydawały się trudne. Pamiętajcie, matematyka to przede wszystkim logiczne myślenie i rozwiązywanie problemów. Powodzenia!