Jak Obliczyć Pojemność Walca W Litrach

W życiu codziennym często spotykamy się z walcami – od puszek konserw, przez beczki, po zbiorniki na wodę. Zrozumienie, jak obliczyć ich pojemność, czyli ile litrów dany walec może pomieścić, jest niezwykle przydatne. W tym artykule, krok po kroku, wyjaśnimy, jak to zrobić, używając prostych wzorów i przykładów.

Co to jest Walec?

Zanim przejdziemy do obliczeń, warto zdefiniować, czym właściwie jest walec. W geometrii, walec to bryła obrotowa ograniczona powierzchnią walcową i dwiema równoległymi podstawami, które są kołami. Wyobraź sobie puszkę – to idealny przykład walca.

Kluczowe Elementy Walca:

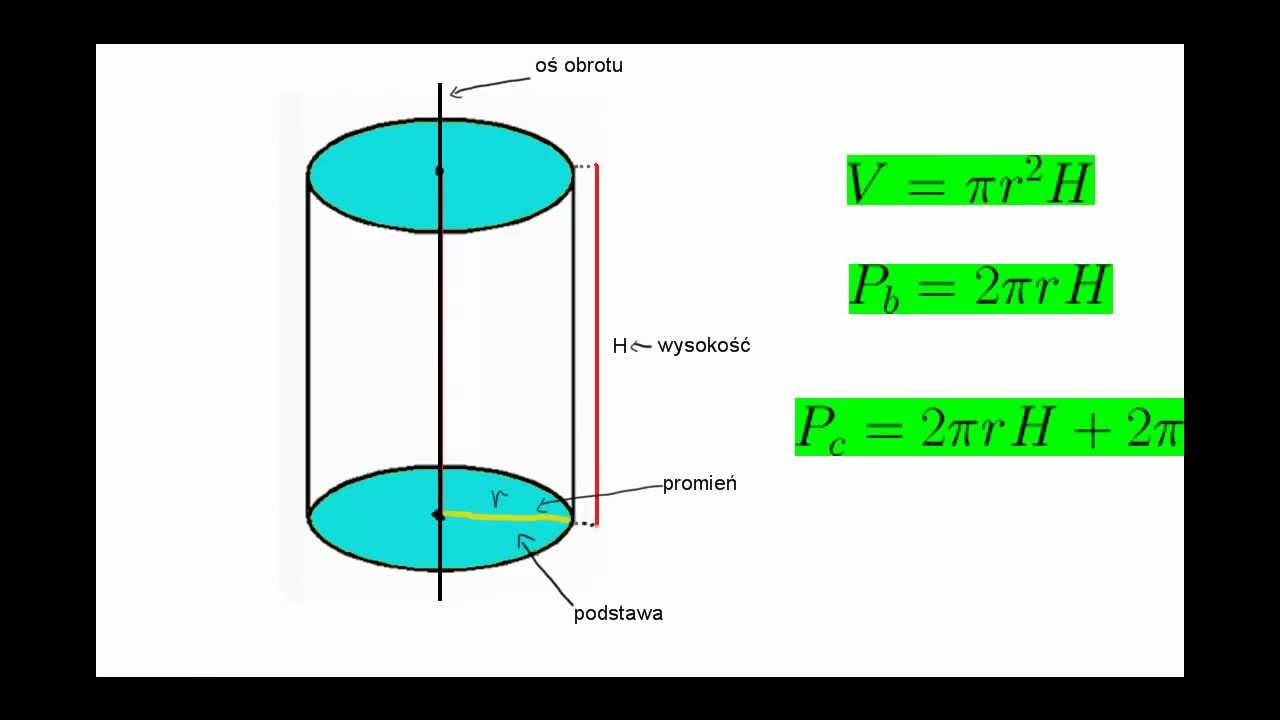
Podstawa: Koło, które stanowi górną i dolną część walca.
Promień (r): Odległość od środka koła do dowolnego punktu na jego obwodzie.
Wysokość (h): Odległość między dwiema podstawami walca.

Wzór na Objętość Walca

Obliczanie pojemności walca zaczyna się od obliczenia jego objętości. Objętość to miara przestrzeni, jaką zajmuje dana bryła. W przypadku walca, objętość obliczamy, mnożąc pole podstawy przez wysokość.

Wzór na objętość walca to:

V = πr²h

Gdzie:

V – objętość walca
π (pi) – stała matematyczna, w przybliżeniu równa 3.14159
r – promień podstawy
h – wysokość walca

Ważne: Upewnij się, że wszystkie wymiary (promień i wysokość) są wyrażone w tej samej jednostce, np. w centymetrach (cm) lub metrach (m).

Krok po Kroku: Obliczanie Objętości

Aby obliczyć objętość walca, wykonaj następujące kroki:

Zmierz promień podstawy (r): Jeśli masz średnicę, podziel ją przez 2, aby otrzymać promień.
Zmierz wysokość walca (h).
Podstaw wartości do wzoru: V = πr²h
Wykonaj obliczenia.

Przykład: Załóżmy, że mamy walec o promieniu 5 cm i wysokości 10 cm. Jak obliczyć jego objętość?

r = 5 cm
h = 10 cm
V = π * (5 cm)² * 10 cm
V = 3.14159 * 25 cm² * 10 cm
V = 785.3975 cm³

Zatem objętość tego walca wynosi około 785.4 cm³.

Przeliczanie Jednostek: Centymetry Kubiczne na Litry

Pamiętaj, że objętość obliczona w centymetrach sześciennych (cm³) nie jest tym samym, co pojemność w litrach (L). Aby przeliczyć centymetry sześcienne na litry, musimy pamiętać o następującej zależności:

1 litr (L) = 1000 centymetrów sześciennych (cm³)

Czyli:

Liczba litrów = Liczba centymetrów sześciennych / 1000

Wracając do naszego przykładu, gdzie objętość walca wynosiła 785.4 cm³, aby obliczyć pojemność w litrach, dzielimy tę wartość przez 1000:

Pojemność = 785.4 cm³ / 1000 = 0.7854 L

Oznacza to, że nasz walec ma pojemność około 0.785 litra.

Przykłady i Praktyczne Zastosowania

Obliczanie pojemności walca ma wiele praktycznych zastosowań. Oto kilka przykładów:

Puszki konserw: Producenci żywności muszą dokładnie znać pojemność puszek, aby prawidłowo etykietować produkty.
Zbiorniki na wodę: Określenie pojemności zbiornika jest kluczowe przy planowaniu systemów nawadniania lub zaopatrzenia w wodę.
Beczki: W przemyśle spożywczym i chemicznym, pojemność beczek jest istotna przy przechowywaniu i transportowaniu różnych substancji.
Cylindry silników: Inżynierowie muszą znać pojemność cylindrów w silnikach spalinowych, aby obliczyć ich moc i wydajność.

Przykład bardziej złożony: Załóżmy, że chcemy zbudować zbiornik na deszczówkę w kształcie walca o średnicy 1 metra i wysokości 1.5 metra. Ile litrów wody zmieści się w takim zbiorniku?

Oblicz promień: Średnica = 1 metr, więc promień r = 0.5 metra.
Wysokość: h = 1.5 metra.
Oblicz objętość w metrach sześciennych (m³): V = π * (0.5 m)² * 1.5 m = 3.14159 * 0.25 m² * 1.5 m = 1.178 m³
Przelicz metry sześcienne na litry: 1 m³ = 1000 litrów, więc V = 1.178 m³ * 1000 L/m³ = 1178 litrów.

Oznacza to, że w takim zbiorniku zmieści się około 1178 litrów wody.

Podsumowanie

Obliczanie pojemności walca w litrach jest stosunkowo proste, jeśli pamiętamy odpowiedni wzór i potrafimy przeliczać jednostki. Kluczem jest prawidłowe zmierzenie promienia i wysokości walca, a następnie zastosowanie wzoru na objętość: V = πr²h. Pamiętaj, aby na koniec przeliczyć jednostki z centymetrów sześciennych (cm³) na litry (L), dzieląc objętość przez 1000. Znajomość tych zasad pozwala na dokładne określenie pojemności różnych przedmiotów i konstrukcji w kształcie walca, co jest przydatne w wielu dziedzinach życia.