Jak Obliczyć Odległość Za Pomocą Współrzędnych Geograficznych

Wyobraź sobie, że stoisz na szczycie wieży Eiffla, a twój przyjaciel wyleguje się na plaży Copacabana. Chcesz wiedzieć, ile kilometrów was dzieli w linii prostej. Jak to obliczyć, mając jedynie współrzędne geograficzne tych dwóch miejsc? Odpowiedź kryje się w matematyce i kilku sprytnych wzorach.

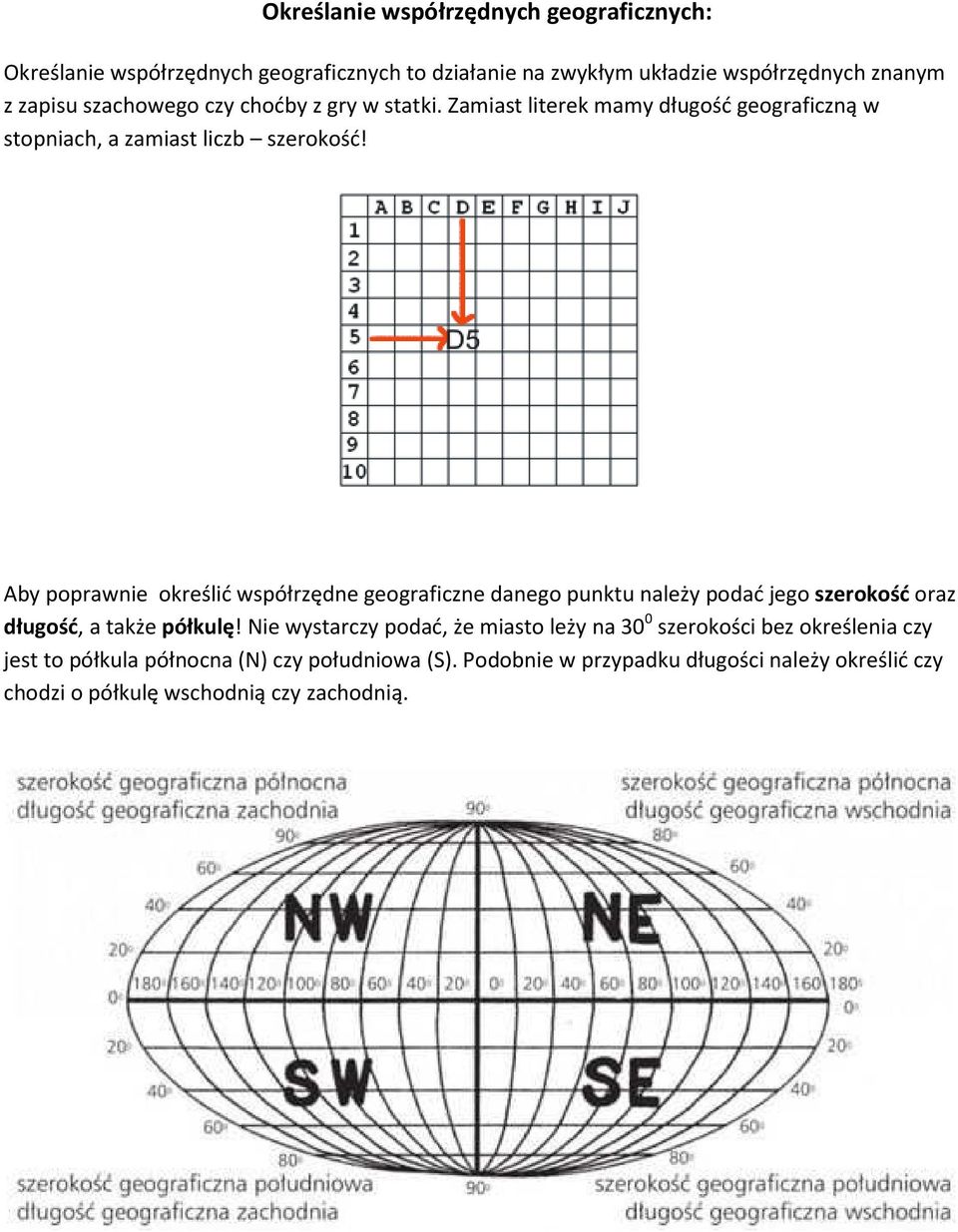
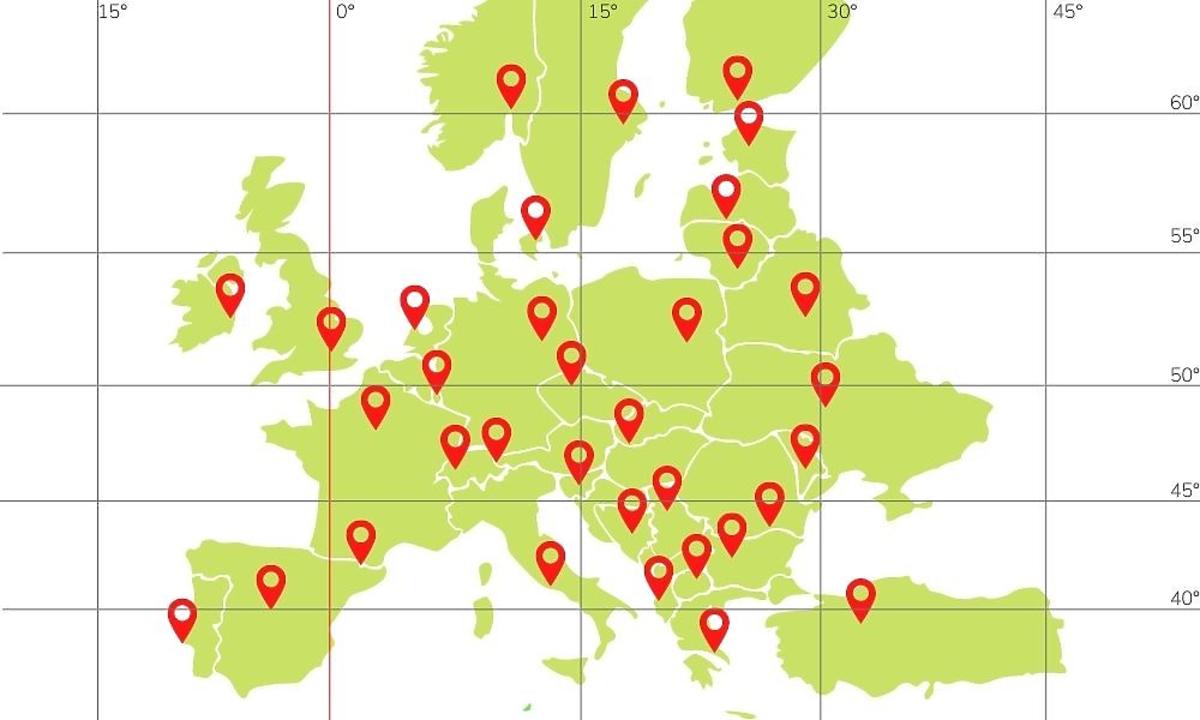
Zanim przejdziemy do sedna, przypomnijmy sobie, czym są współrzędne geograficzne. Każde miejsce na Ziemi można jednoznacznie określić za pomocą dwóch liczb: szerokości geograficznej (latitude) i długości geograficznej (longitude). Szerokość geograficzna to kąt między danym punktem a równikiem, mierzony w stopniach (od -90° na biegunie południowym do +90° na biegunie północnym). Długość geograficzna to kąt między danym punktem a południkiem zerowym (Greenwich), również mierzony w stopniach (od -180° na zachód do +180° na wschód).

Mając te dane, możemy przystąpić do obliczeń.

Wzór Haversine – prosty, ale skuteczny

Jedną z najpopularniejszych metod obliczania odległości między dwoma punktami na sferze (a Ziemia jest bliska sfery) jest wzór Haversine. Wykorzystuje on funkcję haversine, która jest po prostu połową kwadratu sinusa połowy kąta.

Aby użyć tego wzoru, potrzebujemy współrzędnych geograficznych obu punktów w stopniach dziesiętnych (np. 48.8584° N, 2.2945° E dla wieży Eiffla). Oznaczmy współrzędne pierwszego punktu (A) jako (lat1, lon1), a współrzędne drugiego punktu (B) jako (lat2, lon2).

Przelicz stopnie na radiany: Wzór Haversine operuje na radianach, więc musimy najpierw przeliczyć nasze współrzędne z stopni na radiany. Możemy to zrobić, mnożąc wartość w stopniach przez π/180 (gdzie π ≈ 3.14159265359).

lat1 = lat1 * (π/180) lon1 = lon1 * (π/180) lat2 = lat2 * (π/180) lon2 = lon2 * (π/180)
Oblicz różnice: Następnie obliczamy różnice między szerokościami i długościami geograficznymi:

dlat = lat2 - lat1 dlon = lon2 - lon1
Zastosuj wzór Haversine: Teraz możemy wreszcie zastosować wzór Haversine:

a = sin²(dlat/2) + cos(lat1) * cos(lat2) * sin²(dlon/2) c = 2 * atan2(√a, √(1-a)) d = R * c

Gdzie:
- R to promień Ziemi (średnio około 6371 km).
- atan2 to funkcja arcus tangens z dwoma argumentami (uwzględnia znaki argumentów, co daje poprawny wynik w każdym kwadrancie).
- d to odległość między punktami A i B w kilometrach.

Wzór ten, choć wygląda skomplikowanie, jest dość prosty w implementacji i daje dobre wyniki dla większości zastosowań. Pamiętaj, że zakłada on kulisty kształt Ziemi, co wprowadza pewne uproszczenie.

Bardziej precyzyjne metody

Wzór Haversine jest wystarczający dla wielu celów, ale jeśli potrzebujemy większej precyzji, możemy zastosować bardziej zaawansowane metody, które uwzględniają elipsoidalny kształt Ziemi. Ziemia nie jest idealną kulą, lecz elipsoidą spłaszczoną na biegunach. To spłaszczenie ma wpływ na obliczanie odległości, szczególnie na większych dystansach.

Jedną z takich metod jest wzór Vincenty'ego. Jest on bardziej skomplikowany niż wzór Haversine, ale zapewnia znacznie większą dokładność, zwłaszcza dla punktów położonych daleko od siebie. Wzór Vincenty'ego iteracyjnie poprawia wynik, aż osiągnie żądaną precyzję. Implementacja tego wzoru jest bardziej złożona i często wymaga użycia gotowych bibliotek lub funkcji dostępnych w językach programowania.

Należy pamiętać, że nawet najbardziej precyzyjne wzory nie są idealne. Na dokładność obliczeń wpływają również inne czynniki, takie jak niedokładność pomiaru współrzędnych geograficznych oraz lokalne odchylenia od idealnego kształtu Ziemi.

W praktyce – narzędzia i biblioteki

Na szczęście nie musimy za każdym razem pisać kodu od zera. Istnieje wiele narzędzi online oraz bibliotek w różnych językach programowania, które ułatwiają obliczanie odległości na podstawie współrzędnych geograficznych.

Przykłady:

Google Maps API: Umożliwia obliczanie odległości między punktami, uwzględniając elipsoidalny kształt Ziemi i dając bardzo dokładne wyniki. API to jest szczególnie przydatne, gdy potrzebujemy wyznaczyć trasę przejazdu uwzględniającą drogi.
Biblioteki w Pythonie (np. geopy, geographiclib): Oferują gotowe funkcje do obliczania odległości różnymi metodami (w tym Haversine i Vincenty). Są łatwe w użyciu i pozwalają na szybkie zintegrowanie obliczeń odległości z naszymi aplikacjami.
Narzędzia online: Istnieją liczne strony internetowe, które pozwalają na wprowadzenie współrzędnych geograficznych i natychmiastowe obliczenie odległości między nimi. Są to proste i szybkie rozwiązania dla jednorazowych obliczeń.

Korzystanie z gotowych narzędzi i bibliotek znacznie upraszcza proces obliczania odległości i pozwala skupić się na innych aspektach naszego projektu.

Podsumowanie

Obliczanie odległości między dwoma punktami na podstawie ich współrzędnych geograficznych to zagadnienie, które znajduje zastosowanie w wielu dziedzinach, od nawigacji i logistyki po geodezję i astronomię. Wzór Haversine jest prostym i skutecznym rozwiązaniem dla większości zastosowań, natomiast wzór Vincenty'ego oferuje większą precyzję. Dostępne narzędzia i biblioteki ułatwiają implementację tych wzorów i pozwalają na szybkie uzyskanie potrzebnych wyników. Mając tę wiedzę, możesz już bez problemu obliczyć odległość między wieżą Eiffla a plażą Copacabana, albo dowolnymi innymi dwoma miejscami na Ziemi! Pamiętaj, że kluczem do sukcesu jest poprawne przeliczenie stopni na radiany oraz wybór odpowiedniego wzoru w zależności od wymaganej precyzji.