Jak Obliczyć Obwód Trapezu Równoramiennego

Drodzy nauczyciele matematyki!

Trapez równoramienny to figura geometryczna, która często pojawia się na lekcjach geometrii w szkołach podstawowych i ponadpodstawowych. Obliczanie jego obwodu to umiejętność, która wymaga zrozumienia podstawowych właściwości trapezu oraz umiejętności dodawania. W tym artykule przyjrzymy się, jak efektywnie uczyć uczniów, jak obliczać obwód trapezu równoramiennego, jak unikać typowych błędów oraz jak sprawić, by ta lekcja była interesująca i angażująca.

Definicja i Właściwości Trapezu Równoramiennego

Zanim przejdziemy do obliczania obwodu, upewnijmy się, że uczniowie rozumieją, co to jest trapez równoramienny. Trapez równoramienny to czworokąt, który ma jedną parę boków równoległych (podstawy) i boki nierównoległe (ramiona) o równej długości. Ważne cechy trapezu równoramiennego to:

Dwie podstawy (a i b) są równoległe.
Dwa ramiona (c) mają równą długość.
Kąty przy każdej podstawie są równe.

Kluczem do skutecznego nauczania jest wizualizacja. Korzystajcie z rysunków, modeli 3D (jeśli to możliwe) oraz oprogramowania do geometrii, aby uczniowie mogli zobaczyć i dotknąć trapez równoramienny. Możecie poprosić uczniów o znalezienie przykładów trapezu równoramiennego w otaczającym ich świecie – np. w architekturze, meblach czy przedmiotach codziennego użytku.

Jak Obliczyć Obwód Trapezu Równoramiennego

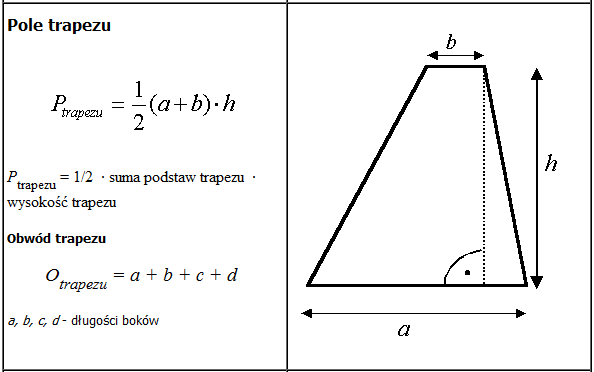
Obwód dowolnej figury geometrycznej to suma długości wszystkich jej boków. W przypadku trapezu równoramiennego, obliczenie obwodu jest stosunkowo proste. Wzór na obwód trapezu równoramiennego to:

Obwód = a + b + 2c

Gdzie:

a to długość jednej podstawy
b to długość drugiej podstawy
c to długość ramienia

Kroki do obliczenia obwodu:

Upewnij się, że znasz długości obu podstaw (a i b) oraz długość ramienia (c).
Podstaw wartości do wzoru: Obwód = a + b + 2c
Wykonaj obliczenia, pamiętając o kolejności działań.
Podaj odpowiedź wraz z jednostką (np. cm, m, mm).

Przykłady Obliczeń

Aby uczniowie lepiej zrozumieli koncepcję, warto rozwiązać kilka przykładów razem z nimi. Oto kilka propozycji:

Przykład 1:

Podstawa a = 5 cm, podstawa b = 9 cm, ramię c = 4 cm.

Obwód = 5 cm + 9 cm + 2 * 4 cm = 5 cm + 9 cm + 8 cm = 22 cm.

Przykład 2:

Podstawa a = 12 m, podstawa b = 20 m, ramię c = 8 m.

Obwód = 12 m + 20 m + 2 * 8 m = 12 m + 20 m + 16 m = 48 m.

Po każdym przykładzie, zachęcaj uczniów do aktywnego udziału, zadając im pytania kontrolne, takie jak:

Co reprezentują poszczególne litery we wzorze?
Jak zmieni się obwód, jeśli zwiększymy długość ramienia?
Czy jednostki muszą być takie same, aby można było wykonać obliczenia?

Typowe Błędy i Jak Ich Unikać

Podczas nauki o obwodzie trapezu równoramiennego, uczniowie często popełniają pewne błędy. Ważne jest, aby być świadomym tych błędów i aktywnie im zapobiegać.

Zapominanie o pomnożeniu długości ramienia przez 2: Uczniowie mogą zapomnieć, że trapez równoramienny ma dwa ramiona o równej długości, więc należy pomnożyć długość ramienia przez 2. Podkreślajcie to w każdym przykładzie i zachęcajcie do zapisywania wzoru w całości.
Mylenie podstaw z ramionami: Ważne jest, aby uczniowie rozumieli, które boki są podstawami, a które ramionami. Wykorzystajcie wizualne pomoce i ćwiczenia, w których uczniowie będą musieli identyfikować poszczególne elementy trapezu.
Dodawanie wszystkich liczb podanych w zadaniu bez zrozumienia: Uczniowie mogą automatycznie dodawać wszystkie liczby, które widzą w zadaniu, bez zastanowienia się, co te liczby oznaczają. Nauczcie ich uważnego czytania zadania i identyfikowania, które informacje są potrzebne do obliczenia obwodu.
Błędy w jednostkach: Uczniowie mogą zapomnieć o podawaniu jednostek lub używać różnych jednostek dla różnych boków. Podkreślajcie znaczenie spójności jednostek i zachęcajcie do zapisywania jednostek przy każdej liczbie.

Aby pomóc uczniom unikać tych błędów, warto:

Stosować kolorowe rysunki i diagramy: Oznaczanie boków różnymi kolorami może pomóc w wizualnym rozróżnieniu podstaw i ramion.
Zachęcać do sprawdzania odpowiedzi: Po obliczeniu obwodu, uczniowie powinni sprawdzić, czy ich odpowiedź ma sens w kontekście zadania.
Dawać dużo przykładów i ćwiczeń: Im więcej przykładów i ćwiczeń rozwiążą uczniowie, tym lepiej utrwalą sobie wiedzę.

Jak Uatrakcyjnić Lekcję

Aby lekcja o obwodzie trapezu równoramiennego była bardziej angażująca i interesująca, warto zastosować różne metody i techniki.

Gry i zabawy: Można zorganizować quizy, gry planszowe lub interaktywne gry online, w których uczniowie będą musieli obliczać obwody trapezu równoramiennego.
Projekty praktyczne: Uczniowie mogą zbudować modele trapezu równoramiennego z papieru, kartonu lub innych materiałów i obliczyć ich obwody.
Zadania z życia wzięte: Można przedstawić zadania, w których uczniowie będą musieli obliczyć obwód trapezu równoramiennego w kontekście rzeczywistych sytuacji, np. obliczanie ilości materiału potrzebnego do obramowania rabaty w kształcie trapezu lub obliczanie długości ogrodzenia wokół działki.
Wykorzystanie technologii: Użycie interaktywnych symulacji lub aplikacji do geometrii może pomóc uczniom w wizualizacji i zrozumieniu koncepcji obwodu.
Praca w grupach: Podzielcie uczniów na mniejsze grupy i dajcie im zadanie do rozwiązania, np. zaprojektowanie trapezu równoramiennego o określonym obwodzie i policzenie długości boków.

Przykład zadania z życia wziętego:

Pan Kowalski chce zbudować rabatę w kształcie trapezu równoramiennego. Podstawa rabaty ma mieć długość 3 metry, druga podstawa 5 metrów, a ramię 2 metry. Ile metrów obrzeża potrzebuje pan Kowalski, aby obramować rabatę?

Podsumowanie

Obliczanie obwodu trapezu równoramiennego to ważna umiejętność, którą uczniowie muszą opanować. Kluczem do sukcesu jest zrozumienie definicji i właściwości trapezu, zapamiętanie wzoru na obwód oraz unikanie typowych błędów. Stosując różnorodne metody nauczania, angażujące zadania i przykłady z życia wzięte, możemy sprawić, że ta lekcja będzie interesująca i efektywna dla wszystkich uczniów. Pamiętajmy o wizualizacji, aktywizowaniu uczniów i dostosowywaniu tempa nauki do indywidualnych potrzeb każdego z nich. Powodzenia!