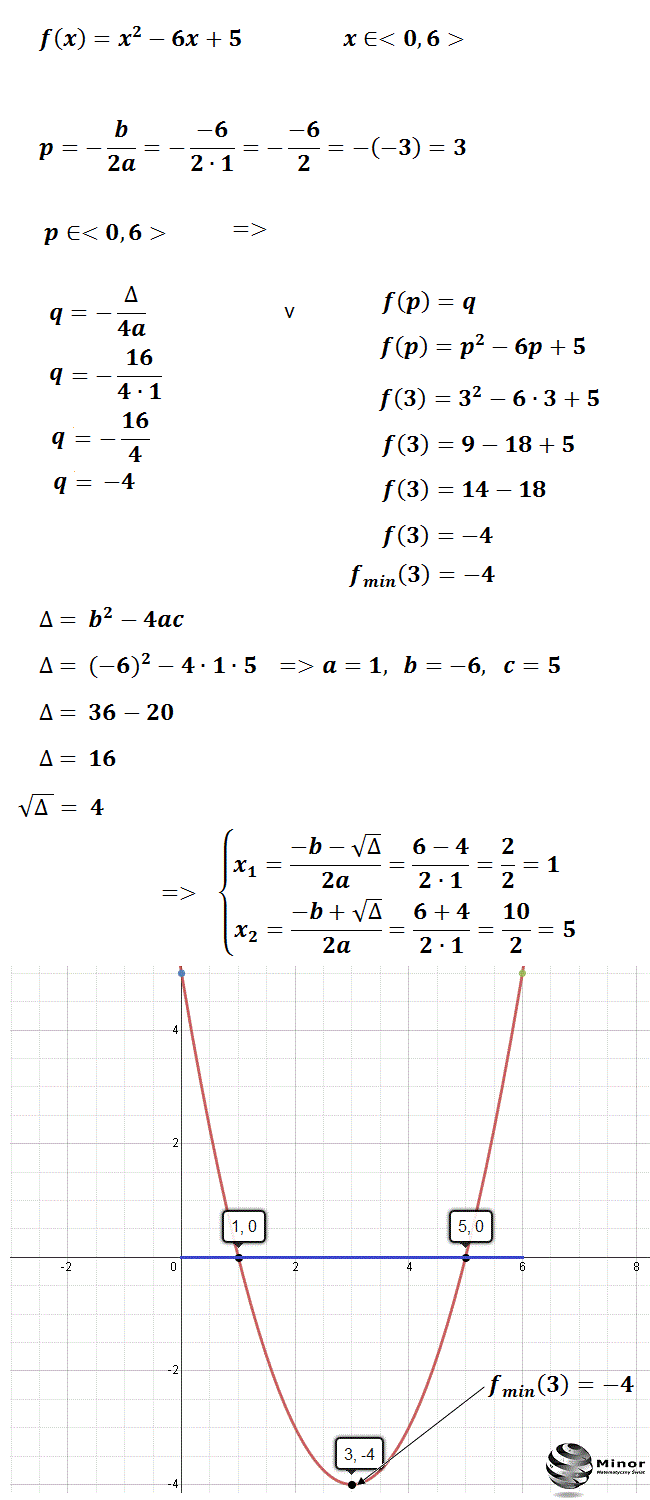Jak Obliczyć Najmniejszą Wartość Funkcji Kwadratowej W Przedziale

Funkcja kwadratowa to potężne narzędzie matematyczne, które znajduje zastosowanie w wielu dziedzinach, od fizyki po ekonomię. Znajomość jej właściwości, w tym umiejętność obliczania wartości minimalnej (lub maksymalnej, w zależności od współczynnika kierunkowego), jest kluczowa. Artykuł ten skupi się na metodach obliczania najmniejszej wartości funkcji kwadratowej w zadanym przedziale.

Zanim przejdziemy do konkretnych obliczeń, przypomnijmy sobie ogólną postać funkcji kwadratowej:

f(x) = ax² + bx + c

Gdzie a, b i c to współczynniki, a 'a' (współczynnik kierunkowy) determinuje, czy parabola (wykres funkcji) jest skierowana ramionami do góry (a > 0) czy do dołu (a < 0). W naszym przypadku, będziemy zakładać, że funkcja ma minimum (a > 0), ponieważ szukamy jej najmniejszej wartości.

Pierwszym krokiem w znalezieniu najmniejszej wartości funkcji kwadratowej jest obliczenie współrzędnej x wierzchołka paraboli. Wierzchołek reprezentuje punkt, w którym funkcja osiąga swoje minimum (dla a > 0) lub maksimum (dla a < 0). Współrzędną x wierzchołka (oznaczaną często jako xw) obliczamy ze wzoru:

xw = -b / 2a

Po obliczeniu xw, możemy obliczyć współrzędną y wierzchołka (yw), która reprezentuje wartość funkcji w tym punkcie:

yw = f(xw) = a(xw)² + b(xw) + c

Teraz, gdy mamy wierzchołek, musimy uwzględnić przedział, w którym szukamy minimum. Załóżmy, że mamy przedział domknięty [p, q], gdzie p i q to liczby rzeczywiste i p <= q. Musimy sprawdzić, czy wierzchołek paraboli (xw) leży wewnątrz tego przedziału.

Jeśli p <= xw <= q, to najmniejsza wartość funkcji w przedziale [p, q] jest po prostu wartością funkcji w wierzchołku, czyli yw. Innymi słowy, minimum globalne funkcji kwadratowej znajduje się w danym przedziale i jest to wartość w wierzchołku.

Jeśli xw nie leży w przedziale [p, q], musimy porównać wartości funkcji na krańcach przedziału, czyli f(p) i f(q). Najmniejszą z tych dwóch wartości będzie najmniejszą wartością funkcji w przedziale [p, q]. Obliczamy więc:

f(p) = a(p)² + b(p) + c f(q) = a(q)² + b(q) + c

Porównujemy f(p) i f(q). Ta wartość, która jest mniejsza, jest najmniejszą wartością funkcji kwadratowej w przedziale [p, q].

Podsumowując kroki:

1. Oblicz xw = -b / 2a.
2. Oblicz yw = f(xw).
3. Sprawdź, czy p <= xw <= q.
   • Jeśli tak, to najmniejsza wartość funkcji w przedziale [p, q] wynosi yw.
   • Jeśli nie, przejdź do kroku 4.
4. Oblicz f(p) i f(q).
5. Porównaj f(p) i f(q). Mniejsza z tych wartości jest najmniejszą wartością funkcji w przedziale [p, q].

Przeanalizujmy kilka przykładów.

Przykład 1:

Funkcja: f(x) = x² - 4x + 5 Przedział: [0, 3]

1. xw = -(-4) / (2 * 1) = 2
2. yw = (2)² - 4(2) + 5 = 4 - 8 + 5 = 1
3. Sprawdzamy, czy 0 <= 2 <= 3. To prawda.

Zatem najmniejsza wartość funkcji f(x) = x² - 4x + 5 w przedziale [0, 3] wynosi 1.

Przykład 2:

Funkcja: f(x) = 2x² + 4x - 1 Przedział: [1, 4]

1. xw = -4 / (2 * 2) = -1

2. yw = 2(-1)² + 4(-1) - 1 = 2 - 4 - 1 = -3

3. Sprawdzamy, czy 1 <= -1 <= 4. To nieprawda.

4. f(1) = 2(1)² + 4(1) - 1 = 2 + 4 - 1 = 5

5. f(4) = 2(4)² + 4(4) - 1 = 32 + 16 - 1 = 47

Porównujemy f(1) = 5 i f(4) = 47. Mniejsza wartość to 5.

Zatem najmniejsza wartość funkcji f(x) = 2x² + 4x - 1 w przedziale [1, 4] wynosi 5.

Przykład 3:

Funkcja: f(x) = x² + 6x + 8 Przedział: [-5, -2]

1. xw = -6 / (2 * 1) = -3
2. yw = (-3)² + 6(-3) + 8 = 9 - 18 + 8 = -1
3. Sprawdzamy, czy -5 <= -3 <= -2. To prawda.

Zatem najmniejsza wartość funkcji f(x) = x² + 6x + 8 w przedziale [-5, -2] wynosi -1.

Dodatkowe Rozważania

Warto zauważyć, że jeśli funkcja kwadratowa jest malejąca w całym przedziale (co może mieć miejsce, gdy wierzchołek leży na prawo od przedziału, a a > 0), to najmniejsza wartość będzie na prawym krańcu przedziału. Analogicznie, jeśli funkcja jest rosnąca w całym przedziale (wierzchołek na lewo od przedziału, a > 0), to najmniejsza wartość będzie na lewym krańcu przedziału. Jednak opisywany algorytm automatycznie uwzględnia te przypadki, porównując wartości na krańcach przedziału.

Ponadto, jeśli przedział jest otwarty (np. (p, q)), procedura obliczeń pozostaje taka sama, z tym wyjątkiem, że teoretycznie najmniejsza wartość nie jest osiągana (funkcja zbliża się do niej dowolnie blisko, ale jej nie osiąga). W praktyce jednak, dla większości zastosowań, wartość obliczona na krańcach domkniętego przedziału jest wystarczająco dobrym przybliżeniem.

Przedział Nieskończony

Co się stanie, gdy przedział jest nieskończony? Załóżmy, że rozważamy przedział [p, +∞).

1. Oblicz xw i yw jak poprzednio.
2. Jeśli p <= xw, to najmniejsza wartość funkcji w przedziale [p, +∞) wynosi yw.
3. Jeśli p > xw, to funkcja jest rosnąca w całym przedziale [p, +∞). W tym przypadku, najmniejsza wartość jest osiągana na lewym krańcu przedziału, czyli w punkcie p. Zatem, oblicz f(p).

Analogicznie, dla przedziału (-∞, q]:

1. Oblicz xw i yw jak poprzednio.
2. Jeśli xw <= q, to najmniejsza wartość funkcji w przedziale (-∞, q] wynosi yw.
3. Jeśli xw > q, to funkcja jest malejąca w całym przedziale (-∞, q]. W tym przypadku, najmniejsza wartość jest osiągana na prawym krańcu przedziału, czyli w punkcie q. Zatem, oblicz f(q).

Pamiętajmy, że w przypadku przedziałów nieskończonych, funkcja może nie mieć wartości najmniejszej (np. gdy a < 0 i rozważamy przedział [p, +∞), funkcja dąży do -∞). W naszych rozważaniach zakładamy, że a > 0 i poszukujemy minimum.

Umiejętność obliczania najmniejszej wartości funkcji kwadratowej w przedziale jest fundamentalną umiejętnością w analizie matematycznej i ma szerokie zastosowanie w rozwiązywaniu problemów optymalizacyjnych. Stosując przedstawione kroki, możemy efektywnie znaleźć poszukiwane minimum, uwzględniając ograniczenia wynikające z zadanego przedziału.