Jak Obliczyć Kąty W Trójkącie Prostokątnym

Czy kiedykolwiek stanąłeś przed problemem obliczenia kątów w trójkącie prostokątnym i poczułeś się zagubiony w gąszczu wzorów i definicji? Wiem, jak to jest! Matematyka potrafi sprawić kłopoty, szczególnie gdy presja rośnie, a potrzebujesz szybko i sprawnie rozwiązać zadanie. Ale nie martw się, ten artykuł powstał właśnie po to, aby rozwiać Twoje wątpliwości i pokazać, że obliczanie kątów w trójkącie prostokątnym wcale nie musi być takie trudne.

Ten poradnik poprowadzi Cię krok po kroku przez różne metody obliczania kątów w trójkącie prostokątnym, niezależnie od tego, jakie dane posiadasz. Zaczniemy od podstawowych definicji i zasad, a następnie przejdziemy do praktycznych przykładów i wskazówek. Przygotuj się na podróż, która sprawi, że matematyka stanie się Twoim sprzymierzeńcem, a nie wrogiem!

Podstawy Trójkąta Prostokątnego

Zanim przejdziemy do konkretnych metod obliczeń, upewnijmy się, że dobrze rozumiemy, czym właściwie jest trójkąt prostokątny. Jest to trójkąt, w którym jeden z kątów jest kątem prostym, czyli ma miarę 90 stopni. Ten kąt oznaczamy zazwyczaj małym kwadratem w rogu trójkąta.

Najdłuższy bok trójkąta prostokątnego, leżący naprzeciwko kąta prostego, nazywamy przeciwprostokątną. Pozostałe dwa boki to przyprostokątne.

Kluczowa zasada: Suma wszystkich kątów w dowolnym trójkącie wynosi zawsze 180 stopni. W trójkącie prostokątnym, skoro jeden kąt ma 90 stopni, suma dwóch pozostałych kątów musi wynosić 90 stopni. Oznacza to, że te dwa kąty są zawsze ostre (czyli mniejsze niż 90 stopni) i dopełniające się (sumują się do 90 stopni).

Metody Obliczania Kątów

Istnieje kilka sposobów na obliczenie kątów w trójkącie prostokątnym. Wybór odpowiedniej metody zależy od tego, jakie dane są nam dostępne.

1. Znając Długości Wszystkich Boków (Funkcje Trygonometryczne)

Jeżeli znamy długości wszystkich trzech boków trójkąta prostokątnego, możemy skorzystać z funkcji trygonometrycznych: sinus (sin), cosinus (cos) i tangens (tan).

Definicje funkcji trygonometrycznych:

Sinus (sin) kąta ostrego = długość przyprostokątnej leżącej naprzeciwko kąta / długość przeciwprostokątnej
Cosinus (cos) kąta ostrego = długość przyprostokątnej leżącej przy kącie / długość przeciwprostokątnej
Tangens (tan) kąta ostrego = długość przyprostokątnej leżącej naprzeciwko kąta / długość przyprostokątnej leżącej przy kącie

Przykład:

Załóżmy, że mamy trójkąt prostokątny, w którym przeciwprostokątna ma długość 5 cm, przyprostokątna leżąca naprzeciwko kąta α ma długość 3 cm, a przyprostokątna leżąca przy kącie α ma długość 4 cm.

Wtedy:

sin(α) = 3/5 = 0.6
cos(α) = 4/5 = 0.8
tan(α) = 3/4 = 0.75

Aby znaleźć miarę kąta α, musimy użyć funkcji arcus sinus (arcsin), arcus cosinus (arccos) lub arcus tangens (arctan) na kalkulatorze (często oznaczane jako sin^-1, cos^-1, tan^-1). Są to funkcje odwrotne do funkcji trygonometrycznych.

W naszym przykładzie:

α = arcsin(0.6) ≈ 36.87 stopni
α = arccos(0.8) ≈ 36.87 stopni
α = arctan(0.75) ≈ 36.87 stopni

Jak widzisz, niezależnie od wybranej funkcji trygonometrycznej, otrzymujemy ten sam wynik (z dokładnością do zaokrągleń).

2. Znając Długość Jednego Boku i Miary Jednego Kąta Ostrego

Jeśli znamy długość jednego boku i miarę jednego kąta ostrego (różnego od kąta prostego), możemy obliczyć miarę drugiego kąta ostrego, korzystając z faktu, że suma kątów ostrych w trójkącie prostokątnym wynosi 90 stopni.

Przykład:

Załóżmy, że w trójkącie prostokątnym kąt α ma miarę 30 stopni. Wtedy kąt β (drugi kąt ostry) ma miarę:

β = 90 stopni - α = 90 stopni - 30 stopni = 60 stopni.

Dodatkowo, znając miarę jednego kąta ostrego i długość jednego boku, możemy obliczyć długości pozostałych boków, ponownie korzystając z funkcji trygonometrycznych.

Przykład:

Załóżmy, że znamy kąt α = 30 stopni i długość przeciwprostokątnej c = 10 cm. Chcemy obliczyć długość przyprostokątnej a (leżącej naprzeciwko kąta α).

Skorzystamy z funkcji sinus:

sin(α) = a / c

sin(30 stopni) = a / 10 cm

a = sin(30 stopni) * 10 cm = 0.5 * 10 cm = 5 cm.

Analogicznie, możemy obliczyć długość drugiej przyprostokątnej b, korzystając z funkcji cosinus.

3. Znając Długości Dwóch Boków

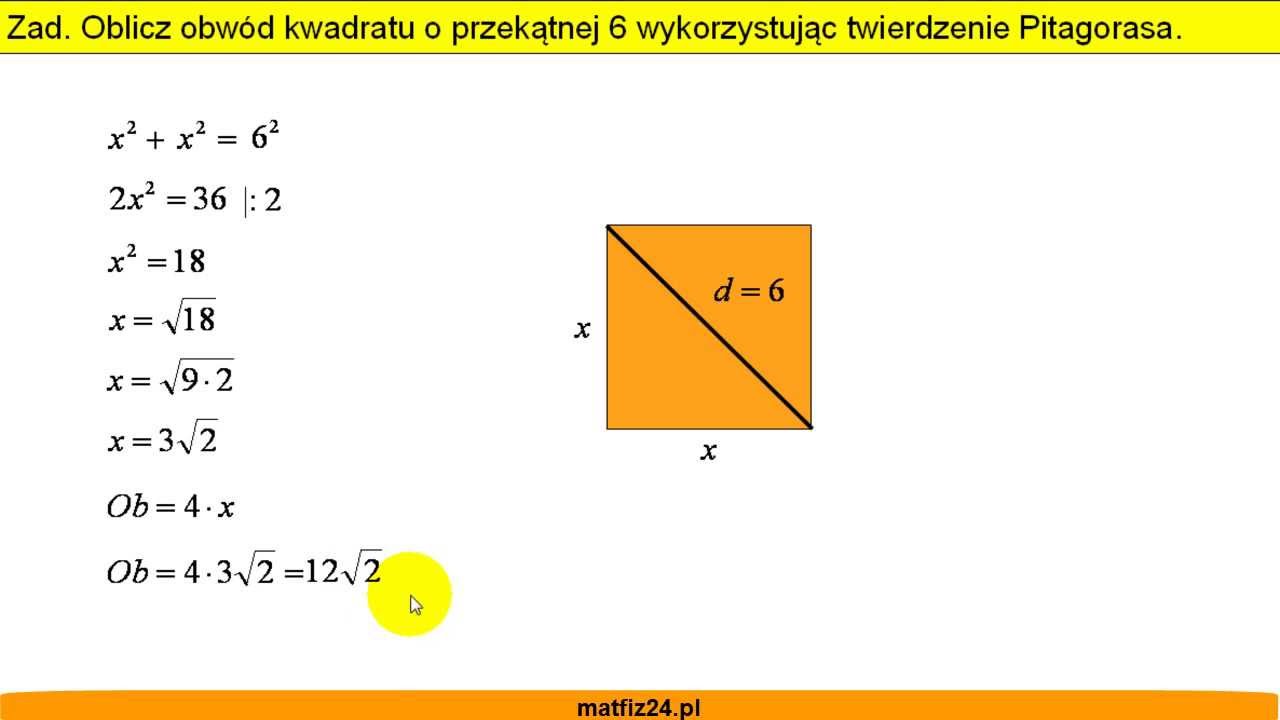
Jeśli znamy długości dwóch boków trójkąta prostokątnego, możemy użyć twierdzenia Pitagorasa, aby obliczyć długość trzeciego boku. Twierdzenie Pitagorasa mówi, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej:

a² + b² = c²

gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej.

Po obliczeniu długości wszystkich trzech boków, możemy skorzystać z funkcji trygonometrycznych (sin, cos, tan) i ich funkcji odwrotnych (arcsin, arccos, arctan), aby obliczyć miary kątów ostrych, jak opisano w punkcie 1.

Przykład:

Załóżmy, że a = 3 cm i b = 4 cm. Wtedy:

c² = 3² + 4² = 9 + 16 = 25

c = √25 = 5 cm.

Teraz, znając długości wszystkich boków, możemy obliczyć miarę kąta α (naprzeciwko boku a) za pomocą funkcji sinus:

sin(α) = a / c = 3/5 = 0.6

α = arcsin(0.6) ≈ 36.87 stopni.

Praktyczne Wskazówki i Pułapki

Upewnij się, że Twój kalkulator jest ustawiony na odpowiedni tryb (stopnie lub radiany). Większość zadań szkolnych i praktycznych wymaga obliczeń w stopniach.
Dokładność: Podczas obliczeń trygonometrycznych staraj się używać jak najwięcej miejsc po przecinku, aby uzyskać dokładniejszy wynik. Zaokrąglaj dopiero na samym końcu obliczeń.
Sprawdź swój wynik: Upewnij się, że suma kątów w trójkącie wynosi 180 stopni. Upewnij się także, że najdłuższy bok (przeciwprostokątna) jest rzeczywiście najdłuższy.
Zrozum, co liczysz: Nie tylko ślepo stosuj wzory. Spróbuj zrozumieć, dlaczego dana funkcja trygonometryczna jest odpowiednia w danym przypadku. Pomoże Ci to uniknąć błędów.
Szkicuj! Zawsze warto narysować trójkąt prostokątny i zaznaczyć na nim znane dane. To pomoże Ci wizualizować problem i uniknąć pomyłek.

Podsumowanie

Obliczanie kątów w trójkącie prostokątnym może wydawać się skomplikowane na początku, ale z odpowiednią wiedzą i praktyką staje się coraz łatwiejsze. Kluczem do sukcesu jest zrozumienie podstawowych definicji i zasad, znajomość funkcji trygonometrycznych oraz umiejętność wykorzystania twierdzenia Pitagorasa.

Pamiętaj, że matematyka to przede wszystkim praktyka. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zasady i tym pewniej będziesz się czuł. Nie bój się pytać o pomoc, korzystać z dostępnych zasobów online i offline, a przede wszystkim – nie poddawaj się! Powodzenia!

"Matematyka jest kluczem do ukrytych drzwi wszechświata." - Galileo Galilei (Ta cytat, choć może trochę patetyczny, przypomina, że matematyka ma ogromne znaczenie i może być źródłem satysfakcji.)