Jak Obliczyć Bok Trapezu Prostokątnego

Kto by pomyślał, że liczenie boków trapezu prostokątnego może być... zabawne? No dobra, może nie od razu zwijać się ze śmiechu, ale obiecuję, że postaram się, żeby to nie było nudne jak flaki z olejem. Wyobraź sobie trapez prostokątny jako dziwaczną konstrukcję, jakby ktoś nie do końca umiał zbudować normalny dom, a potem się poddał i zostawił go w połowie.

Jak to ugryźć?

Do dzieła! Załóżmy, że chcesz obliczyć długość boku, który nie jest ani podstawą, ani wysokością. Czyli tego pochyłego. Spokojnie, to nie jest fizyka kwantowa. Potrzebujesz do tego minimalnej wiedzy z Pitagorasa, tego gościa od a² + b² = c². Pamiętasz go, prawda? Mam nadzieję, że tak, bo inaczej cała nasza konstrukcja runie jak domek z kart!

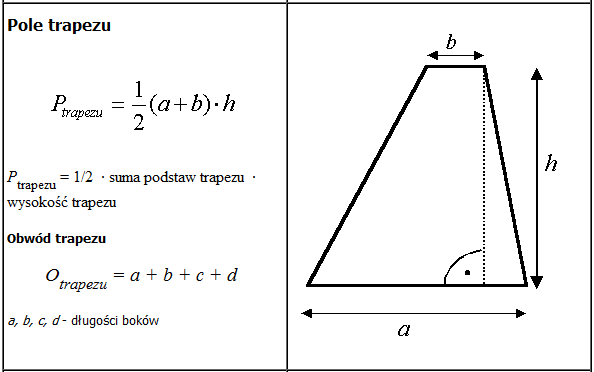
Najpierw musimy sprowadzić naszego trapez do prostokąta i trójkąta prostokątnego. Narysuj sobie ten trapez. Potem, z wierzchołka krótszej podstawy poprowadź prostą linię prostopadłą do dłuższej podstawy. Voila! Masz prostokąt i trójkąt. Ten bok trapezu, którego szukasz, jest teraz przeciwprostokątną w naszym nowo powstałym trójkącie.

Potrzebne składniki

Aby skorzystać z twierdzenia Pitagorasa, potrzebujemy znać długości dwóch pozostałych boków trójkąta. Jedna długość to wysokość trapezu – ta sama, co bok w naszym prostokącie. Druga długość to różnica między długościami podstaw trapezu. Czyli, jeśli dłuższa podstawa ma 10 cm, a krótsza 6 cm, to ta różnica wynosi 4 cm. Ot i cała filozofia!

Mając te dwie wartości, możemy użyć magicznego wzoru: a² + b² = c². Gdzie a to wysokość trapezu, b to różnica długości podstaw, a c to szukana długość boku trapezu (nasza przeciwprostokątna).

Praktyka czyni mistrza

Załóżmy, że wysokość trapezu wynosi 3 cm, a różnica długości podstaw 4 cm. Wtedy:

3² + 4² = c²

9 + 16 = c²

25 = c²

Teraz musimy wyciągnąć pierwiastek kwadratowy z 25. I tu wkracza do akcji kalkulator (chyba, że jesteś mistrzem obliczeń w pamięci – szacunek!). Pierwiastek kwadratowy z 25 to 5.

Zatem, długość pochyłego boku trapezu wynosi 5 cm! Hurra! Udało się! Możesz świętować. Może kawałek ciasta? Albo spacer na świeżym powietrzu? Zasłużyłeś!

Trochę refleksji na koniec

Widzisz? To wcale nie było takie straszne. Matematyka czasem wygląda groźnie, ale pod tą fasadą kryje się logika i piękno. A czasem po prostu zwykłe liczenie boków trapezu, które, przyznaj szczerze, może się kiedyś przydać. Może przy budowie karmnika dla ptaków? Albo tworzeniu abstrakcyjnej rzeźby? Kto wie!

Pamiętaj, matematyka to nie tylko suche wzory. To narzędzie, które pozwala nam zrozumieć świat wokół nas. A zrozumienie świata to całkiem niezła zabawa, prawda?

A jeśli nadal czujesz się niepewnie, zawsze możesz poprosić o pomoc Pitagorasa... No dobra, może nie osobiście, ale w internecie znajdziesz mnóstwo materiałów i ćwiczeń. Powodzenia!