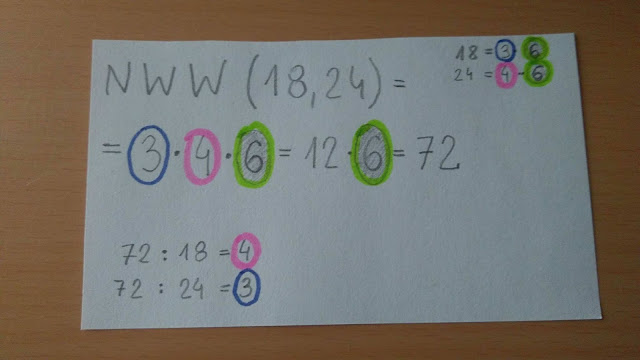Jak Oblicza Sie Nww I Nwd

Zmagasz się z zadaniem, w którym musisz znaleźć Największy Wspólny Dzielnik (NWD) lub Najmniejszą Wspólną Wielokrotność (NWW) dwóch lub więcej liczb? Nie martw się! Wielu uczniów i dorosłych napotyka trudności w zrozumieniu tych koncepcji. Celem tego artykułu jest rozjaśnienie tych zagadnień i pokazanie, jak krok po kroku, obliczać NWD i NWW, nawet jeśli matematyka nie jest Twoją mocną stroną.

Czym Właściwie Jest NWD i NWW?

Zanim przejdziemy do obliczeń, upewnijmy się, że rozumiemy, czym właściwie są NWD i NWW. Pomyśl o nich jak o dwóch stronach tej samej monety – oba odnoszą się do relacji między liczbami, ale robią to w różny sposób.

Największy Wspólny Dzielnik (NWD)

NWD, jak sama nazwa wskazuje, to największa liczba, która dzieli bez reszty dwie lub więcej liczb. Można to sobie wyobrazić jako "wspólnego przodka" tych liczb w sensie podzielności. Na przykład, NWD liczb 12 i 18 to 6, ponieważ 6 jest największą liczbą, przez którą można podzielić zarówno 12, jak i 18, uzyskując liczbę całkowitą.

Najmniejsza Wspólna Wielokrotność (NWW)

Z kolei NWW to najmniejsza liczba, która jest wielokrotnością dwóch lub więcej liczb. Inaczej mówiąc, to najmniejsza liczba, którą można podzielić przez każdą z tych liczb, uzyskując liczbę całkowitą. Dla przykładu, NWW liczb 4 i 6 to 12, ponieważ 12 jest najmniejszą liczbą, którą można podzielić zarówno przez 4, jak i przez 6, bez reszty.

Metody Obliczania NWD

Istnieją różne metody znajdowania NWD, a wybór najlepszej zależy często od liczb, z którymi pracujemy. Oto dwie najpopularniejsze metody:

Metoda Wypisywania Dzielników

Ta metoda jest szczególnie przydatna dla małych liczb. Polega ona na wypisaniu wszystkich dzielników każdej liczby, a następnie znalezieniu największego dzielnika, który występuje we wszystkich listach.

Przykład: Oblicz NWD liczb 12 i 18.

Dzielniki liczby 12: 1, 2, 3, 4, 6, 12

Dzielniki liczby 18: 1, 2, 3, 6, 9, 18

Największym dzielnikiem, który występuje w obu listach, jest 6. Zatem NWD(12, 18) = 6.

Algorytm Euklidesa

Algorytm Euklidesa to wydajna metoda obliczania NWD, szczególnie przydatna dla większych liczb. Opiera się ona na powtarzanym dzieleniu z resztą.

Kroki algorytmu:

1. Podziel większą liczbę przez mniejszą i znajdź resztę.
2. Jeśli reszta jest równa 0, to mniejsza liczba jest NWD.
3. Jeśli reszta jest różna od 0, zastąp większą liczbę mniejszą liczbą, a mniejszą liczbę resztą.
4. Powtarzaj kroki 1-3, aż reszta będzie równa 0.

Przykład: Oblicz NWD liczb 48 i 18.

1. 48 : 18 = 2 reszty 12
2. 18 : 12 = 1 reszty 6
3. 12 : 6 = 2 reszty 0

Ponieważ reszta jest równa 0, NWD(48, 18) = 6.

Metody Obliczania NWW

Podobnie jak w przypadku NWD, istnieje kilka metod obliczania NWW.

Metoda Wypisywania Wielokrotności

Ta metoda jest podobna do metody wypisywania dzielników, ale zamiast dzielników, wypisujemy wielokrotności każdej liczby, aż znajdziemy wspólną wielokrotność. Następnie wybieramy najmniejszą z nich.

Przykład: Oblicz NWW liczb 4 i 6.

Wielokrotności liczby 4: 4, 8, 12, 16, 20, 24...

Wielokrotności liczby 6: 6, 12, 18, 24, 30...

Najmniejszą wspólną wielokrotnością jest 12. Zatem NWW(4, 6) = 12.

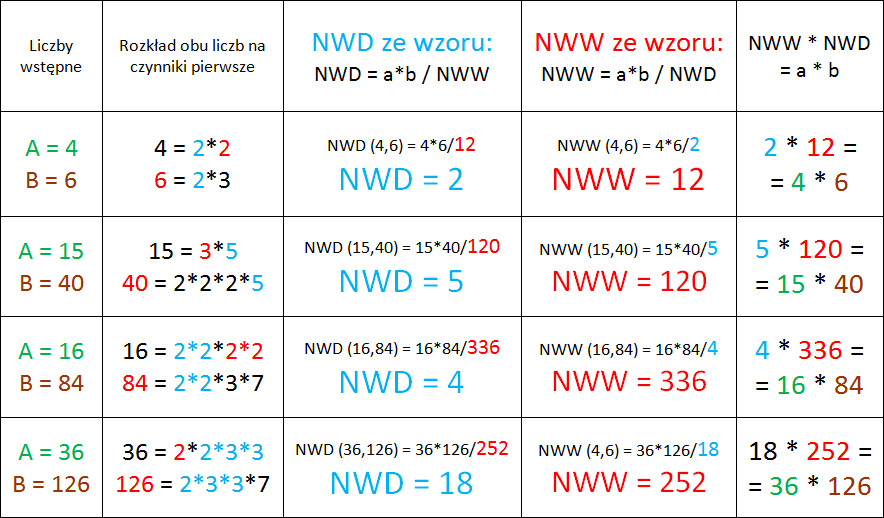
Metoda z Wykorzystaniem NWD

Istnieje prosty związek między NWD i NWW, który można wykorzystać do obliczenia NWW, jeśli znamy NWD dwóch liczb. Wzór jest następujący:

NWW(a, b) = (|a * b|) / NWD(a, b)

Oznacza to, że NWW dwóch liczb jest równe wartości bezwzględnej iloczynu tych liczb podzielonej przez ich NWD.

Przykład: Oblicz NWW liczb 12 i 18, wiedząc, że NWD(12, 18) = 6.

NWW(12, 18) = (|12 * 18|) / 6 = 216 / 6 = 36

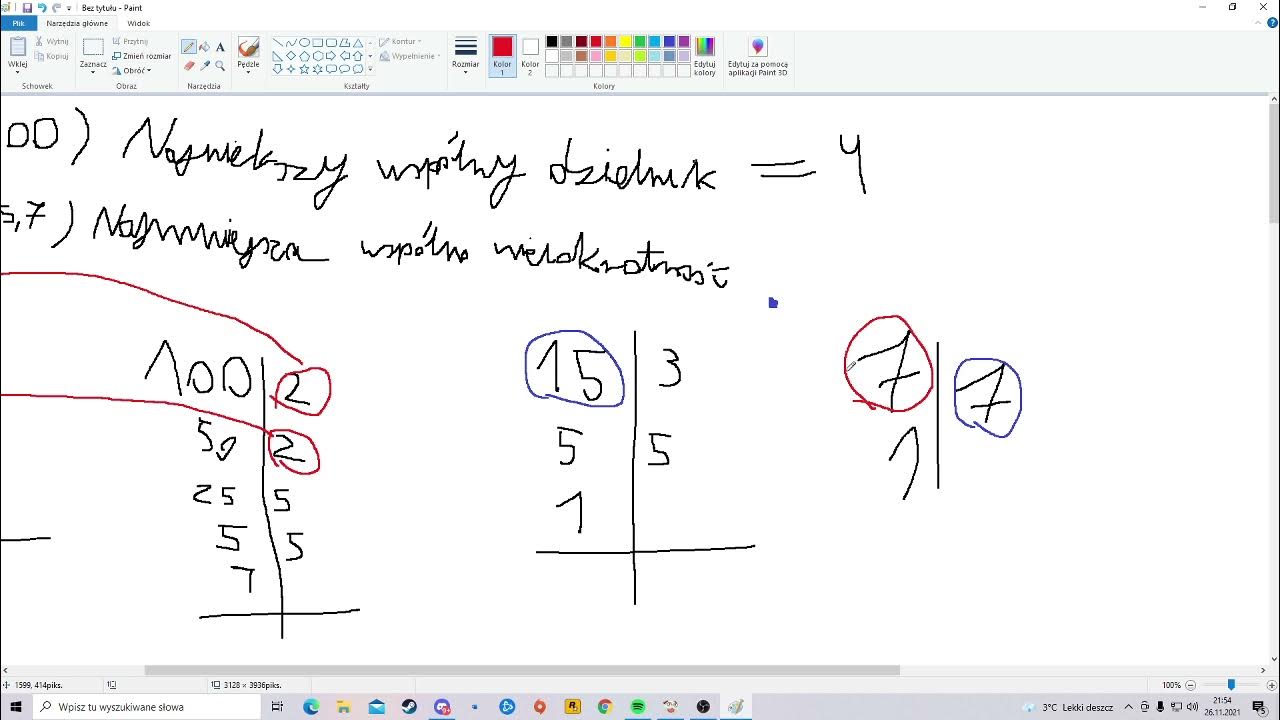
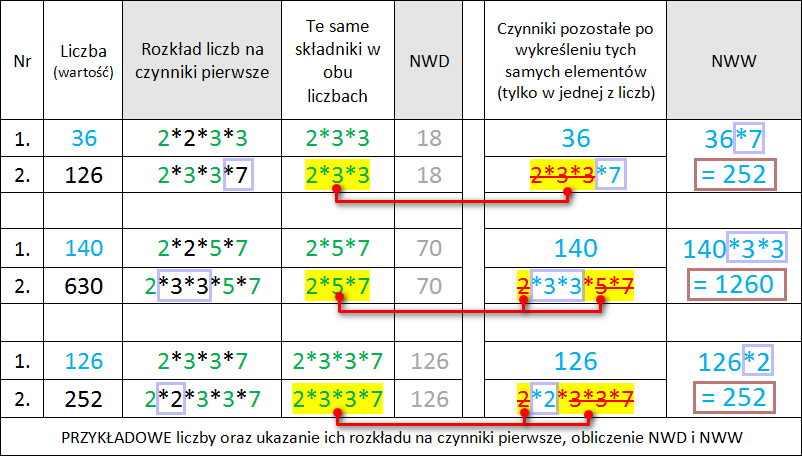
Rozkład na Czynniki Pierwsze

Ta metoda jest szczególnie przydatna, gdy mamy do czynienia z większymi liczbami lub chcemy zrozumieć strukturę liczbową. Polega ona na rozłożeniu każdej liczby na czynniki pierwsze, a następnie zbudowaniu NWW, biorąc najwyższe potęgi każdego czynnika pierwszego występującego w rozkładach.

Przykład: Oblicz NWW liczb 24 i 36.

Rozkład na czynniki pierwsze:

24 = 2³ * 3

36 = 2² * 3²

NWW(24, 36) = 2³ * 3² = 8 * 9 = 72

Praktyczne Zastosowania NWD i NWW

NWD i NWW to nie tylko abstrakcyjne pojęcia matematyczne. Mają one wiele praktycznych zastosowań w różnych dziedzinach, w tym:

• Upraszczanie ułamków: NWD licznika i mianownika pozwala na uproszczenie ułamka do postaci nieskracalnej.
• Podział zasobów: NWD może pomóc w równym podziale zasobów na grupy. Na przykład, jeśli masz 24 jabłka i 36 pomarańczy, NWD (24, 36) = 12 powie Ci, że możesz stworzyć 12 identycznych paczek, każda zawierająca 2 jabłka i 3 pomarańcze.
• Planowanie: NWW może być używane do planowania powtarzających się wydarzeń. Na przykład, jeśli autobus A kursuje co 15 minut, a autobus B co 20 minut, to NWW (15, 20) = 60 powie Ci, że autobusy spotkają się na tym samym przystanku co 60 minut.
• Kryptografia: NWD i NWW, a także pojęcia z nimi związane, są wykorzystywane w niektórych algorytmach kryptograficznych.

Podsumowanie

Obliczanie NWD i NWW może wydawać się trudne na początku, ale dzięki zrozumieniu podstawowych koncepcji i zastosowaniu odpowiednich metod, zadanie to staje się o wiele prostsze. Pamiętaj o różnych metodach i wybierz tę, która najlepiej pasuje do liczb, z którymi pracujesz. Ćwicz regularnie, a wkrótce będziesz mistrzem NWD i NWW!

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, jak obliczać NWD i NWW. Nie bój się eksperymentować z różnymi metodami i znaleźć tę, która najlepiej Ci odpowiada. Powodzenia!