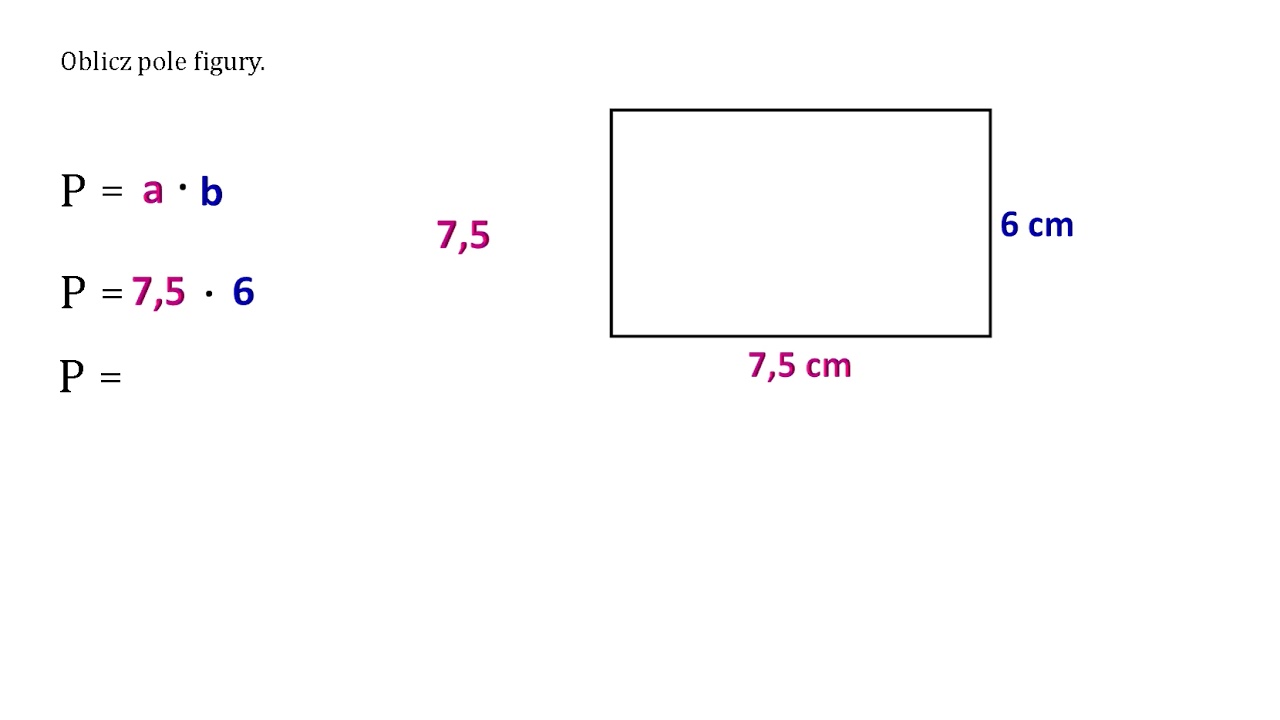
Jak Liczy Się Pole Równoległoboku

Czy kiedykolwiek patrzyłeś na dach domu, dziwny kształt kwiatka na łące, albo nawet na kostkę czekolady i pomyślałeś: "Ciekawe, ile to zajmuje miejsca?" Obliczenie powierzchni różnych figur to nie tylko abstrakcyjna matematyka – to praktyczna umiejętność, która przydaje się w wielu sytuacjach życiowych. Dziś skupimy się na obliczaniu pola równoległoboku, figury, która choć na pierwszy rzut oka może wydawać się skomplikowana, w rzeczywistości kryje w sobie prostą i elegancką zasadę.

Dlaczego Pole Równoległoboku Jest Ważne?

Zanim zagłębimy się w wzory i obliczenia, zastanówmy się chwilę, dlaczego w ogóle warto poświęcić czas na zrozumienie tego zagadnienia. Obliczenie pola równoległoboku ma szerokie zastosowanie w różnych dziedzinach:

Architektura i budownictwo: Projektowanie dachów, fasad budynków, obliczanie ilości materiałów potrzebnych do pokrycia powierzchni.
Geodezja i kartografia: Określanie powierzchni działek, mapowanie terenów.
Projektowanie wnętrz: Obliczanie ilości tapet, farby, paneli podłogowych potrzebnych do wykończenia pomieszczenia.
Gry komputerowe i grafika: Tworzenie realistycznych środowisk, obliczanie powierzchni tekstur.
Nawet w życiu codziennym: Ocena wielkości dywanu, który chcemy kupić, lub porównywanie powierzchni dwóch działek.

Zrozumienie, jak liczy się pole równoległoboku, otwiera drzwi do rozwiązywania wielu praktycznych problemów. To nie tylko wiedza teoretyczna, ale realna umiejętność, która może ułatwić Ci życie.

Co To Jest Równoległobok?

Zanim przejdziemy do obliczeń, upewnijmy się, że dobrze rozumiemy, czym właściwie jest równoległobok. Najprościej mówiąc, to czworokąt, który ma dwie pary boków równoległych. To oznacza, że boki naprzeciwległe są nie tylko równoległe, ale również równe długości. Równoległobokiem jest między innymi kwadrat i prostokąt, ale nie każdy równoległobok jest kwadratem lub prostokątem – boki mogą nie tworzyć kątów prostych.

Jak Obliczyć Pole Równoległoboku – Prosta Formuła

Teraz do sedna! Obliczenie pola równoległoboku jest zaskakująco proste. Potrzebujemy tylko dwóch wartości:

Podstawa (a): Dowolny z boków równoległoboku możemy uznać za podstawę.
Wysokość (h): Wysokość to odległość między podstawą a bokiem do niej równoległym, mierzona prostopadle do podstawy. Ważne jest, aby pamiętać, że wysokość nie jest długością boku równoległoboku, chyba że jest to prostokąt.

Mając te dwie wartości, możemy zastosować prosty wzór:

Pole (P) = podstawa (a) * wysokość (h)

Czyli: P = a * h

To wszystko! Pomnóż długość podstawy przez wysokość, a otrzymasz pole równoległoboku.

Przykład:

Załóżmy, że mamy równoległobok, którego podstawa ma długość 8 cm, a wysokość opuszczona na tę podstawę wynosi 5 cm. Jakie jest pole tego równoległoboku?

P = a * h = 8 cm * 5 cm = 40 cm²

Pole równoległoboku wynosi 40 centymetrów kwadratowych.

Dlaczego To Działa? – Wyjaśnienie Intuicyjne

Możesz się zastanawiać, dlaczego ten wzór działa. Wyobraź sobie, że z równoległoboku odcinamy trójkąt prostokątny z jednego boku i doklejamy go do drugiego boku. W ten sposób otrzymujemy... prostokąt! Prostokąt ma dokładnie taką samą podstawę i wysokość jak równoległobok, a wiemy, jak obliczyć pole prostokąta (podstawa * wysokość). Zatem pole równoległoboku jest takie samo jak pole prostokąta, który możemy z niego utworzyć.

Pułapki i Jak Ich Unikać

Podczas obliczania pola równoległoboku można popełnić kilka typowych błędów. Oto kilka pułapek i wskazówki, jak ich unikać:

Pomylenie wysokości z długością boku: Wysokość nie jest długością boku, chyba że równoległobok jest prostokątem. Zawsze szukaj odległości między podstawą a bokiem do niej równoległym, mierzonej prostopadle do podstawy.
Użycie nieprawidłowych jednostek: Upewnij się, że podstawa i wysokość są wyrażone w tej samej jednostce (np. centymetry, metry, cale). Jeśli tak nie jest, musisz najpierw zamienić jedną z wartości, zanim wykonasz obliczenia. Pamiętaj, że pole wyrażone jest w jednostkach kwadratowych (np. cm², m², cale²).
Błędne pomiary: Dokładność pomiarów ma kluczowe znaczenie dla prawidłowego obliczenia pola. Używaj precyzyjnych narzędzi pomiarowych i upewnij się, że mierzysz odległość prostopadle do podstawy.
Zapominanie o wzorze: Choć wzór jest prosty, łatwo o nim zapomnieć. Zapisz go sobie i miej go pod ręką podczas rozwiązywania zadań.

Alternatywne Metody (Dla bardziej zaawansowanych)

Choć wzór P = a * h jest najprostszy i najczęściej stosowany, istnieją również inne metody obliczania pola równoległoboku, które mogą być przydatne w pewnych sytuacjach. Na przykład:

Znając długości dwóch sąsiednich boków i kąt między nimi: Jeśli znasz długości dwóch sąsiednich boków (a i b) oraz kąt (α) między nimi, możesz użyć wzoru: P = a * b * sin(α). Pamiętaj, że kąt α musi być wyrażony w stopniach lub radianach, w zależności od kalkulatora lub programu, którego używasz.
Za pomocą wektorów: Jeśli masz dane współrzędne wierzchołków równoległoboku, możesz obliczyć pole za pomocą iloczynu wektorowego. Jest to metoda bardziej zaawansowana, ale przydatna w geometrii analitycznej.

Te alternatywne metody mogą być przydatne, gdy nie znasz wysokości równoległoboku, ale masz inne dane.

Counterpoints – Co Jeśli Równoległobok Jest Skomplikowany?

Możesz pomyśleć: "Łatwo liczyć pole, gdy mam idealny rysunek. Ale co, jeśli mam skomplikowany kształt, który tylko *przypomina* równoległobok?" To świetne pytanie! W rzeczywistości wiele realnych obiektów ma nieregularne kształty, które tylko w przybliżeniu przypominają figury geometryczne. W takich przypadkach możemy zastosować następujące strategie:

Przybliżenie: Możemy spróbować przybliżyć kształt do idealnego równoległoboku i obliczyć jego pole. Im lepsze przybliżenie, tym dokładniejszy wynik.
Podział na mniejsze figury: Możemy podzielić skomplikowany kształt na mniejsze figury, których pola potrafimy obliczyć (np. trójkąty, prostokąty). Następnie sumujemy pola tych mniejszych figur, aby otrzymać przybliżone pole całego kształtu.
Metody numeryczne: W przypadku bardzo skomplikowanych kształtów możemy użyć metod numerycznych, takich jak metoda Monte Carlo, aby oszacować pole.

Pamiętaj, że w realnych sytuacjach często musimy zaakceptować pewien margines błędu. Ważne jest, aby zrozumieć ograniczenia naszych obliczeń i umieć ocenić, czy uzyskany wynik jest wystarczająco dokładny dla danego zastosowania.

Podsumowanie i Następne Kroki

Gratulacje! Przeszliśmy przez wszystkie najważniejsze aspekty obliczania pola równoległoboku. Teraz wiesz, czym jest równoległobok, jak obliczyć jego pole za pomocą prostego wzoru (P = a * h), jak unikać typowych błędów i jakie są alternatywne metody obliczania pola. Pamiętaj, że praktyka czyni mistrza! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz tę koncepcję.

Zastanów się teraz, gdzie w swoim otoczeniu możesz znaleźć równoległoboki. Czy widzisz je w architekturze, designie, czy może w przyrodzie? Spróbuj oszacować ich pola. Pomyśl, jak ta nowa wiedza może Ci się przydać w przyszłości.

Czy jesteś gotowy, aby zmierzyć się z kolejnym wyzwaniem geometrycznym? Co powiesz na obliczanie pola trapezu?