Jak Dzielić Pisemnie Ułamki Dziesiętne

Czy kiedykolwiek stanęliście przed problemem, jak podzielić pisemnie ułamki dziesiętne i poczuliście się zagubieni? Spokojnie, to uczucie jest powszechne. Matematyka, zwłaszcza ta bardziej zaawansowana, potrafi być frustrująca. Ale uwierzcie mi, dzielenie pisemne ułamków dziesiętnych, choć na pierwszy rzut oka wydaje się skomplikowane, w rzeczywistości opiera się na kilku prostych zasadach. Kluczem jest zrozumienie tych zasad i praktyka.

Wyobraźcie sobie, że pieczecie ciasto. Przepis wymaga podzielenia składników na równe porcje. Albo planujecie podróż i musicie obliczyć, ile kilometrów przejedziecie każdego dnia. W obu tych sytuacjach, umiejętność dzielenia ułamków dziesiętnych pisemnie okazuje się nieoceniona. To nie tylko abstrakcyjna wiedza z podręcznika – to narzędzie, które pomaga nam w codziennym życiu.

Niektórzy mogą argumentować, że w dobie kalkulatorów i arkuszy kalkulacyjnych, uczenie się dzielenia pisemnego jest stratą czasu. Owszem, te narzędzia są przydatne, ale nie zawsze dostępne. Co więcej, zrozumienie, jak działa dzielenie pisemne, pozwala na lepsze zrozumienie samych ułamków dziesiętnych i matematyki w ogóle. To buduje solidne fundamenty, które przydadzą się w dalszej nauce i rozwiązywaniu bardziej złożonych problemów.

Krok po Kroku: Dzielenie Pisemne Ułamków Dziesiętnych

Przejdźmy teraz do konkretów. Jak zatem dzielić pisemnie ułamki dziesiętne? Oto szczegółowa instrukcja:

1. Ustalenie Dzielnika i Dzielnej

Pierwszym krokiem jest ustalenie, co jest dzielną (czyli liczbą, którą dzielimy) i co jest dzielnikiem (czyli liczbą, przez którą dzielimy). Na przykład, w działaniu 12,5 ÷ 2,5, 12,5 jest dzielną, a 2,5 jest dzielnikiem.

2. Pozbycie się Przecinka z Dzielnika

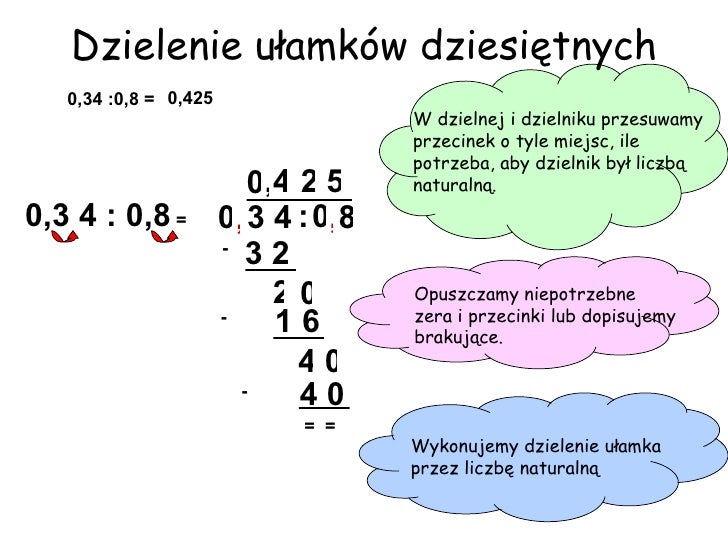
Kluczową zasadą jest pozbycie się przecinka z dzielnika. Robimy to, przesuwając przecinek w dzielniku w prawo o tyle miejsc, aby otrzymać liczbę całkowitą. Jednocześnie, o tyle samo miejsc musimy przesunąć przecinek w dzielnej. Jeśli w dzielnej brakuje cyfr, dopisujemy zera.

Na przykład, jeśli mamy działanie 12,5 ÷ 2,5, przesuwamy przecinek w dzielniku (2,5) o jedno miejsce w prawo, otrzymując 25. W dzielnej (12,5) również przesuwamy przecinek o jedno miejsce w prawo, otrzymując 125. Teraz mamy działanie 125 ÷ 25.

Jeśli natomiast mamy działanie 3 ÷ 0,05, przesuwamy przecinek w dzielniku (0,05) o dwa miejsca w prawo, otrzymując 5. W dzielnej (3) dopisujemy dwa zera i przesuwamy przecinek o dwa miejsca w prawo, otrzymując 300. Teraz mamy działanie 300 ÷ 5.

3. Dzielenie Pisemne Liczb Całkowitych

Po pozbyciu się przecinka z dzielnika, możemy przystąpić do standardowego dzielenia pisemnego liczb całkowitych. Jeśli nie pamiętasz, jak to się robi, przypomnij sobie podstawy – dzielimy krok po kroku, zapisując wynik nad kreską i odejmując od reszty.

W przykładzie 125 ÷ 25, dzielimy 125 przez 25. 25 mieści się w 125 pięć razy (5 x 25 = 125). Zatem wynik to 5.

W przykładzie 300 ÷ 5, dzielimy 300 przez 5. 5 mieści się w 30 sześć razy (6 x 5 = 30). Zostaje nam zero. Dopisujemy kolejne zero i 5 mieści się w 0 zero razy. Zatem wynik to 60.

4. Przecinek w Wyniku

Jeśli po przesunięciu przecinka w dzielnej nadal mamy ułamek dziesiętny, kontynuujemy dzielenie, dopisując zera po przecinku w dzielnej i kontynuując dzielenie pisemne. Przecinek w wyniku stawiamy w tym samym miejscu, co przecinek w dzielnej.

Na przykład, jeśli mamy działanie 7,5 ÷ 2, przesuwamy przecinek w dzielniku, otrzymując 2. Przesuwamy przecinek w dzielnej, otrzymując 75. Dzielimy 75 przez 2. 2 mieści się w 7 trzy razy (3 x 2 = 6). Zostaje nam 1. Dopisujemy 5. 2 mieści się w 15 siedem razy (7 x 2 = 14). Zostaje nam 1. Dopisujemy zero po przecinku. 2 mieści się w 10 pięć razy (5 x 2 = 10). Zatem wynik to 3,75.

Przykłady Działań

• Przykład 1: 25,6 ÷ 3,2
  • Przesuwamy przecinek w dzielniku i dzielnej o jedno miejsce: 256 ÷ 32
  • Dzielimy 256 przez 32: wynik to 8
• Przykład 2: 1,44 ÷ 0,12
  • Przesuwamy przecinek w dzielniku i dzielnej o dwa miejsca: 144 ÷ 12
  • Dzielimy 144 przez 12: wynik to 12
• Przykład 3: 5 ÷ 0,4
  • Przesuwamy przecinek w dzielniku i dzielnej o jedno miejsce: 50 ÷ 4
  • Dzielimy 50 przez 4: 4 mieści się w 5 jeden raz (1 x 4 = 4). Zostaje nam 1. Dopisujemy 0. 4 mieści się w 10 dwa razy (2 x 4 = 8). Zostaje nam 2. Dopisujemy 0 po przecinku. 4 mieści się w 20 pięć razy (5 x 4 = 20). Zatem wynik to 12,5

Typowe Błędy i Jak Ich Unikać

Podczas dzielenia pisemnego ułamków dziesiętnych, często popełniane są pewne błędy. Oto kilka z nich i sposoby, jak ich unikać:

• Błąd: Zapominanie o przesunięciu przecinka w dzielnej.
  • Rozwiązanie: Zawsze pamiętaj, aby przesunąć przecinek w dzielnej o tyle samo miejsc, co w dzielniku.
• Błąd: Źle umieszczony przecinek w wyniku.
  • Rozwiązanie: Upewnij się, że przecinek w wyniku znajduje się w odpowiednim miejscu, czyli w tym samym miejscu, co przecinek w dzielnej (po przesunięciu).
• Błąd: Błędy w dzieleniu pisemnym liczb całkowitych.
  • Rozwiązanie: Upewnij się, że dobrze znasz algorytm dzielenia pisemnego liczb całkowitych. W razie potrzeby powtórz podstawy.

Praktyczne Ćwiczenia

Najlepszym sposobem na opanowanie dzielenia pisemnego ułamków dziesiętnych jest praktyka. Oto kilka ćwiczeń, które możesz wykonać:

• 15,6 ÷ 1,3
• 2,88 ÷ 0,24
• 7 ÷ 0,5
• 10,5 ÷ 2,5
• 3,6 ÷ 0,09

Sprawdź swoje odpowiedzi, korzystając z kalkulatora. Pamiętaj, że celem nie jest tylko uzyskanie poprawnego wyniku, ale przede wszystkim zrozumienie procesu dzielenia pisemnego.

Alternatywne Metody

Oprócz tradycyjnego dzielenia pisemnego, istnieją również inne metody dzielenia ułamków dziesiętnych. Jedną z nich jest zamiana ułamków dziesiętnych na ułamki zwykłe, a następnie podzielenie ułamków zwykłych. Ta metoda może być przydatna, jeśli dobrze znasz zasady działania na ułamkach zwykłych.

Na przykład, 2,5 ÷ 0,5 można zapisać jako 2 ¹/₂ ÷ ¹/₂. Zamieniamy ułamki mieszane na niewłaściwe: ⁵/₂ ÷ ¹/₂. Dzielenie ułamków zwykłych to mnożenie przez odwrotność: ⁵/₂ x ²/₁ = ¹⁰/₂ = 5.

Warto jednak pamiętać, że dzielenie pisemne ułamków dziesiętnych jest uniwersalną metodą, która sprawdza się w większości przypadków i jest łatwiejsza do zastosowania dla bardziej złożonych liczb.

Podsumowanie

Dzielenie pisemne ułamków dziesiętnych to umiejętność, która może wydawać się trudna na początku, ale z odpowiednią praktyką staje się prosta i intuicyjna. Pamiętaj o kluczowych zasadach: pozbyciu się przecinka z dzielnika, przesunięciu przecinka w dzielnej i poprawnym umieszczeniu przecinka w wyniku. Unikaj typowych błędów i regularnie ćwicz. Zrozumienie tej metody nie tylko pomoże Ci w rozwiązywaniu zadań matematycznych, ale również w wielu sytuacjach życiowych, gdzie precyzyjne obliczenia są niezbędne.

Zatem, czy jesteście gotowi, aby podjąć wyzwanie i udoskonalić swoje umiejętności w dzieleniu pisemnym ułamków dziesiętnych? Jakie działania sprawiają Wam najwięcej trudności i jakie metody okazały się dla Was najbardziej skuteczne? Pamiętajcie, że praktyka czyni mistrza!