Ile Wynosi Suma Kątów W Trapezie

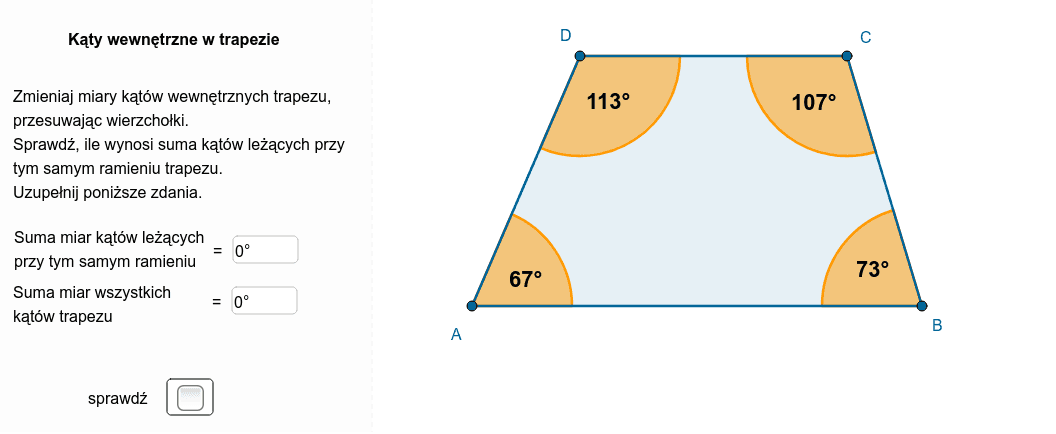
Czy kiedykolwiek zastanawiałeś się, dlaczego matematyka wydaje się tak abstrakcyjna? Często problemem nie jest sama matematyka, ale sposób, w jaki jest prezentowana. Jeśli szukasz odpowiedzi na pytanie, ile wynosi suma kątów w trapezie, jesteś we właściwym miejscu! Obiecuję, że rozwieję wszelkie wątpliwości i pokażę, że geometria może być fascynująca i zrozumiała.

W tym artykule, krok po kroku, przeprowadzimy Cię przez zagadnienie sumy kątów w trapezie. Zaczniemy od podstaw, wyjaśniając czym w ogóle jest trapez, a następnie przejdziemy do dowodu i praktycznych przykładów. Bez zbędnego skomplikowania i używając języka, który zrozumiesz.

Czym jest trapez? Krótkie wprowadzenie

Zanim zagłębimy się w sumę kątów, upewnijmy się, że wszyscy mówimy tym samym językiem. Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych. Te równoległe boki nazywamy podstawami trapezu. Pozostałe dwa boki, które nie są równoległe, nazywamy ramionami trapezu.

Trapez może występować w różnych odmianach:

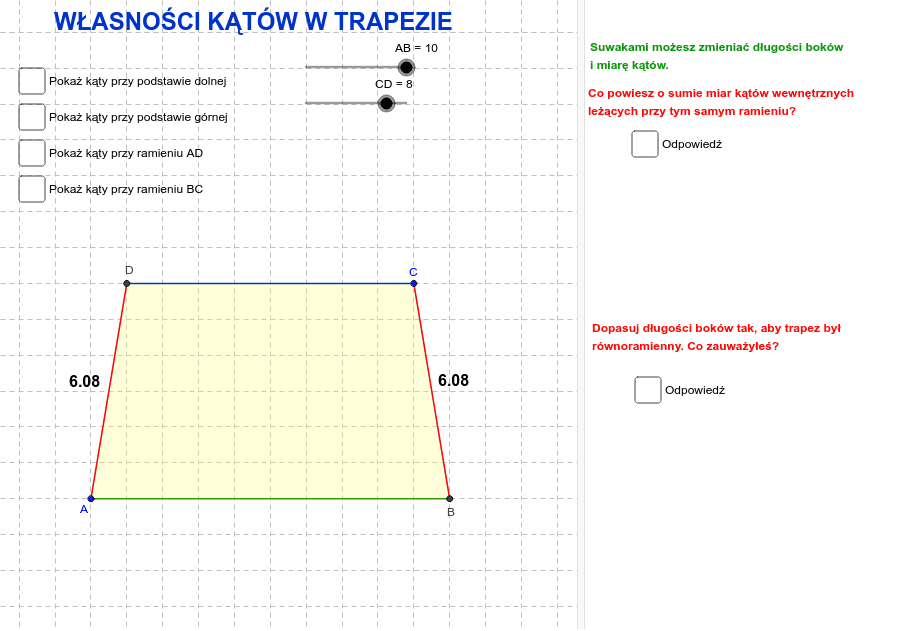
• Trapez równoramienny: Jego ramiona są równej długości.
• Trapez prostokątny: Ma co najmniej jeden kąt prosty.
• Trapez różnoboczny: Wszystkie jego boki mają różną długość.

Rozpoznawanie różnych typów trapezów jest kluczowe do zrozumienia jego właściwości, a co za tym idzie, do obliczania sumy jego kątów.

Suma kątów w dowolnym czworokącie

Zanim przejdziemy do trapezu, przypomnijmy sobie ważną zasadę: suma kątów wewnętrznych w dowolnym czworokącie wynosi 360 stopni. To fundamentalne twierdzenie, które wykorzystamy do zrozumienia sumy kątów w trapezie. Pomyśl o tym, jak o fundamencie, na którym zbudujemy całą naszą wiedzę.

Dlaczego tak jest? Możemy podzielić dowolny czworokąt na dwa trójkąty. Suma kątów w każdym trójkącie wynosi 180 stopni. Zatem dwa trójkąty w czworokącie dają nam 2 * 180 = 360 stopni.

Suma kątów przyległych do ramienia trapezu

Tutaj zaczyna się sedno sprawy. W trapezie, ze względu na równoległość podstaw, pojawia się pewna specyficzna właściwość. Suma kątów przyległych do każdego ramienia trapezu wynosi 180 stopni.

Dlaczego tak jest? Dowód

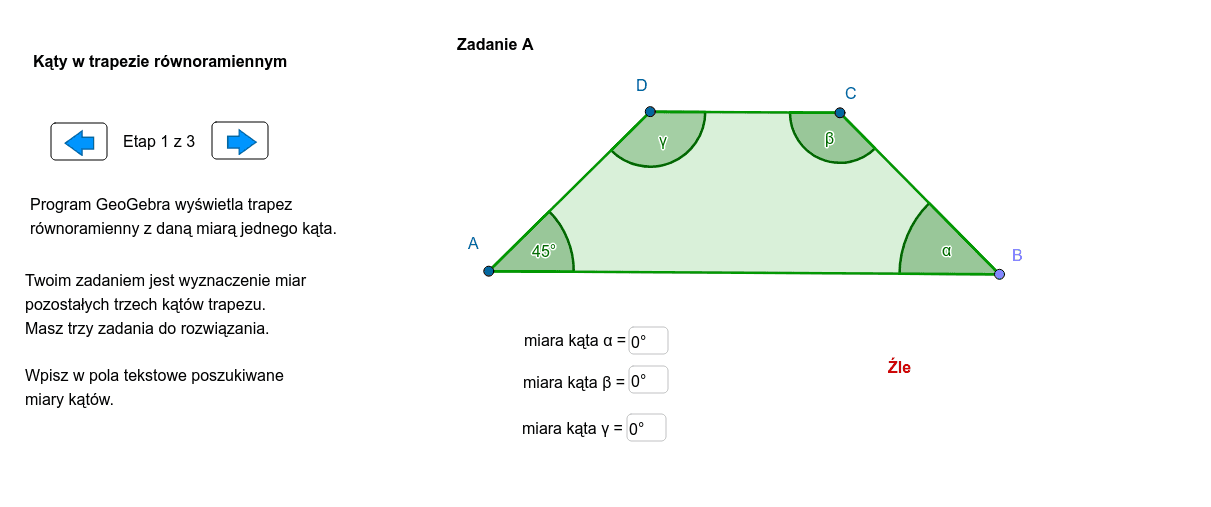
Wyobraźmy sobie trapez ABCD, gdzie AB i CD są podstawami (AB || CD), a AD i BC są ramionami. Kąty przy ramieniu AD to kąt DAB (α) i kąt ADC (β). Chcemy udowodnić, że α + β = 180°.

Możemy przedłużyć bok AD i poprowadzić linię równoległą do AD, przechodzącą przez punkt C. Nazwijmy punkt przecięcia tej linii z przedłużeniem boku AB punktem E. W ten sposób otrzymujemy równoległobok AECD.

W równoległoboku kąty przeciwległe są równe. Zatem kąt AEC = kąt ADC = β. Kąt DAB = α.

Ponieważ AE jest linią prostą, kąt α + kąt AEC = 180° (kąty przyległe). Zastępując kąt AEC kątem β, otrzymujemy α + β = 180°.

Analogicznie, suma kątów przy ramieniu BC również wynosi 180 stopni. Oznacza to, że kąt ABC (γ) + kąt BCD (δ) = 180°.

Konkluzja: Suma wszystkich kątów w trapezie

Wiemy już, że suma kątów przyległych do każdego ramienia trapezu wynosi 180 stopni. A mamy dwa ramiona! Zatem:

Suma wszystkich kątów w trapezie = (suma kątów przy jednym ramieniu) + (suma kątów przy drugim ramieniu) = 180° + 180° = 360°.

Zatem, niezależnie od rodzaju trapezu, suma jego kątów zawsze wynosi 360 stopni! To ważna i uniwersalna zasada.

Przykłady i zastosowania

Zobaczmy teraz, jak tę wiedzę wykorzystać w praktyce. Rozważmy kilka przykładów:

Przykład 1: Trapez równoramienny

Załóżmy, że w trapezie równoramiennym ABCD kąt DAB = 70°. Ponieważ jest to trapez równoramienny, kąt ABC również wynosi 70°. Wiemy, że kąt ADC + kąt DAB = 180°, więc kąt ADC = 180° - 70° = 110°. Podobnie, kąt BCD = 110°. Sprawdźmy: 70° + 70° + 110° + 110° = 360°.

Przykład 2: Trapez prostokątny

W trapezie prostokątnym ABCD, kąt DAB = 90° i kąt ADC = 90°. Załóżmy, że kąt ABC = 60°. Wtedy kąt BCD = 360° - (90° + 90° + 60°) = 120°.

Zastosowania praktyczne

Wiedza o sumie kątów w trapezie może być przydatna w wielu sytuacjach, np. w architekturze, inżynierii i projektowaniu. Pozwala na precyzyjne obliczenia i planowanie przestrzenne. Wyobraź sobie projektowanie dachu o nietypowym kształcie – znajomość właściwości trapezów okaże się nieoceniona!

Wskazówki i triki na zapamiętanie

Jak zapamiętać, że suma kątów w trapezie wynosi 360 stopni?

• Pamiętaj o czworokącie: Trapez to czworokąt, a suma kątów w każdym czworokącie wynosi 360 stopni.
• Podziel na trójkąty: Wyobraź sobie podział trapezu na dwa trójkąty, co wizualnie potwierdza, że suma kątów to 2 * 180 = 360 stopni.
• Kąty przyległe do ramienia: Pamiętaj, że suma kątów przyległych do ramienia trapezu to 180 stopni.

Podsumowanie

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, ile wynosi suma kątów w trapezie. Pamiętaj, że kluczem do sukcesu w matematyce jest zrozumienie podstawowych zasad i umiejętność ich zastosowania w praktyce. Nie bój się zadawać pytań i eksplorować! Matematyka, choć czasem wydaje się trudna, jest fascynującą dziedziną, która otwiera drzwi do zrozumienia świata.

Suma kątów w trapezie zawsze wynosi 360 stopni. To fundamentalna zasada, którą warto zapamiętać. Teraz, uzbrojony w tę wiedzę, możesz śmiało rozwiązywać zadania i analizować geometryczne kształty!

Powodzenia!