Ile Stopni Ma Trapez Równoramienny

Trapez równoramienny. Samo to słowo może wywoływać dreszcze u niejednego ucznia. Geometria potrafi być wyzwaniem, a figury geometryczne, z ich właściwościami i kątami, potrafią sprawić, że zadanie wydaje się trudne do rozwiązania. Ale nie martw się! Rozumiemy Twoje frustracje. Niejedna osoba zmagała się z kątami w trapezie równoramiennym, i wcale nie jest to powód do wstydu. W tym artykule postaramy się to wszystko wytłumaczyć w prosty i przystępny sposób, abyś zrozumiał, o co w tym wszystkim chodzi. Zapomnij o trudnych wzorach – skupimy się na logice i zrozumieniu.

Kąty w Trapezie – Podstawowe Fakty

Zanim przejdziemy do trapezu równoramiennego, przypomnijmy sobie, co to w ogóle jest trapez i jakie ma właściwości:

Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych. Boki te nazywamy podstawami trapezu.
Pozostałe dwa boki, które nie są równoległe, nazywamy ramionami trapezu.
Suma kątów wewnętrznych w każdym czworokącie, w tym w trapezie, wynosi 360 stopni.

Zwróć uwagę na sumę kątów przy jednym ramieniu trapezu. Zawsze wynosi ona 180 stopni. To kluczowa informacja, którą wykorzystamy dalej.

Czym Wyróżnia się Trapez Równoramienny?

Trapez równoramienny, jak sama nazwa wskazuje, jest szczególnym rodzajem trapezu. Co go wyróżnia?

Ramiona trapezu równoramiennego są równe. To bardzo ważne!
Kąty przy tej samej podstawie są równe. To kolejna, kluczowa cecha.

To właśnie równość kątów przy podstawie jest tym, co ułatwia obliczenia. Wyobraź sobie trapez równoramienny jako trapez "symetryczny".

Ile Stopni Mają Kąty w Trapezie Równoramiennym?

To zależy! Nie ma jednej, uniwersalnej odpowiedzi. Miary kątów w trapezie równoramiennym zależą od konkretnego trapezu. Możemy jednak ustalić pewne zasady:

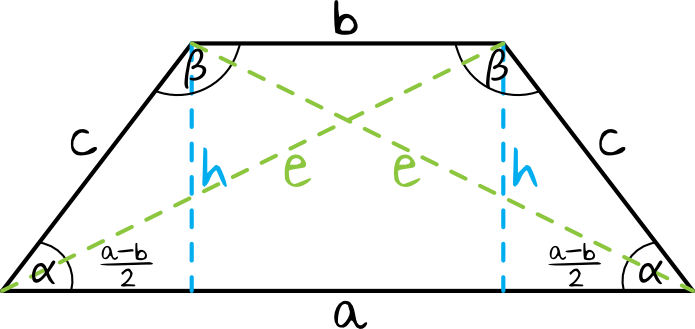
Mamy dwa kąty o tej samej mierze przy jednej podstawie (nazwijmy je α).
Mamy dwa kąty o tej samej mierze przy drugiej podstawie (nazwijmy je β).
Suma wszystkich kątów wynosi 360 stopni: 2α + 2β = 360 stopni.
Suma kątów przy jednym ramieniu wynosi 180 stopni: α + β = 180 stopni.

Dlatego, jeśli znamy miarę jednego kąta w trapezie równoramiennym, możemy obliczyć miary pozostałych kątów. To ogromne ułatwienie!

Przykład 1:

Załóżmy, że jeden z kątów przy podstawie trapezu równoramiennego ma miarę 60 stopni (α = 60°). Ile stopni mają pozostałe kąty?

Skoro α = 60°, to drugi kąt przy tej samej podstawie również ma 60 stopni.
Wiemy, że α + β = 180°, więc β = 180° - 60° = 120°.
Zatem dwa kąty przy drugiej podstawie mają po 120 stopni.

Wniosek: Kąty w tym trapezie równoramiennym to 60°, 60°, 120° i 120°.

Przykład 2:

Jeden z kątów przy podstawie trapezu równoramiennego ma miarę 135 stopni (α = 135°). Ile stopni mają pozostałe kąty?

Skoro α = 135°, to drugi kąt przy tej samej podstawie również ma 135 stopni.
Wiemy, że α + β = 180°, więc β = 180° - 135° = 45°.
Zatem dwa kąty przy drugiej podstawie mają po 45 stopni.

Wniosek: Kąty w tym trapezie równoramiennym to 135°, 135°, 45° i 45°.

Dlaczego To Takie Ważne? Realne Zastosowania

Możesz się zastanawiać, po co w ogóle zawracać sobie głowę kątami w trapezie równoramiennym. Okazuje się, że ta wiedza ma swoje zastosowania w realnym świecie:

Architektura i budownictwo: Trapezy (w tym równoramienne) pojawiają się w projektach architektonicznych, na przykład w dachach budynków, oknach czy elementach dekoracyjnych. Znajomość kątów pozwala na precyzyjne projektowanie i konstruowanie.
Inżynieria: W projektowaniu mostów, ramp i innych konstrukcji inżynierskich wykorzystuje się wiedzę o właściwościach geometrycznych trapezów.
Grafika komputerowa i gry: Trapezy są wykorzystywane do tworzenia trójwymiarowych obiektów i scen w grach komputerowych i programach graficznych.
Sztuka i design: Trapezy i inne figury geometryczne są często wykorzystywane w sztuce i designie, nadając kompozycjom harmonię i równowagę.

Wyobraź sobie projektanta, który musi zaprojektować dach w kształcie trapezu równoramiennego. Bez wiedzy o kątach i ich zależnościach, projekt byłby niedokładny, a konstrukcja mogłaby być niestabilna. To tylko jeden z przykładów, jak geometria wpływa na nasze otoczenie.

Przeciwności i Wątpliwości

Niektórzy mogą argumentować, że geometria to tylko abstrakcyjna teoria, która nie ma większego znaczenia w życiu codziennym. Uważają, że ważniejsze są praktyczne umiejętności, takie jak programowanie czy obsługa maszyn.

Jednak takie podejście jest krótkowzroczne. Wiedza o geometrii rozwija umiejętność logicznego myślenia, rozwiązywania problemów i analizowania informacji. To umiejętności, które są cenne w wielu dziedzinach życia, nie tylko w matematyce i naukach ścisłych. Ponadto, jak wspomniano wcześniej, geometria ma swoje konkretne zastosowania w architekturze, inżynierii i innych dziedzinach.

Inni mogą uważać, że nauka geometrii jest zbyt trudna i wymagająca. Faktycznie, geometria może być wyzwaniem, zwłaszcza dla osób, które mają trudności z abstrakcyjnym myśleniem. Jednak z odpowiednim podejściem i metodami nauczania, każdy może zrozumieć podstawowe zasady geometrii. Kluczem jest zrozumienie, a nie zapamiętywanie wzorów.

Rozwiązania i Dalsze Kroki

Jeśli nadal masz trudności z trapezami równoramiennymi, oto kilka wskazówek:

Rysuj! Zawsze rysuj trapez równoramienny, zaznaczaj dane i szukane kąty. Wizualizacja problemu ułatwia jego rozwiązanie.
Korzystaj z własności: Pamiętaj o równości ramion i kątów przy podstawie. To klucz do rozwiązania wielu zadań.
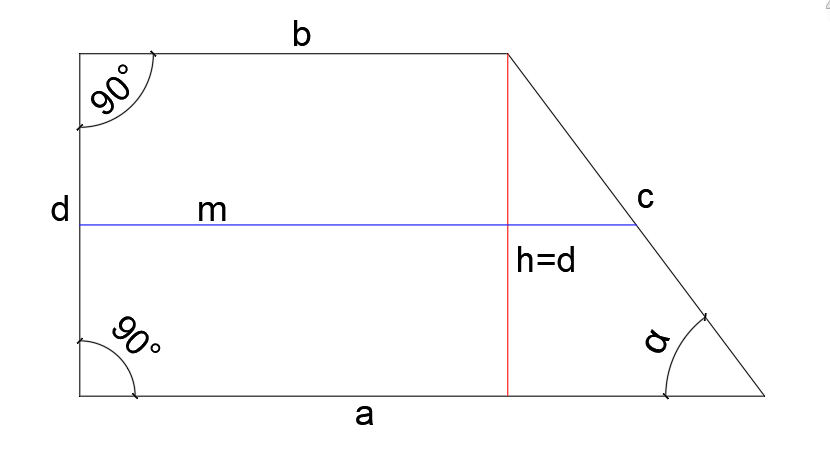
Podziel trapez: Czasami warto podzielić trapez na prostokąt i dwa trójkąty prostokątne. To może ułatwić obliczenia.
Ćwicz! Rozwiązuj różne zadania, zaczynając od prostych przykładów. Im więcej ćwiczysz, tym lepiej zrozumiesz temat.
Szukaj pomocy: Nie wstydź się prosić o pomoc nauczyciela, korepetytora lub kolegów z klasy. Wspólna praca ułatwia naukę.

Dodatkowo, warto skorzystać z dostępnych zasobów online: oglądać filmy edukacyjne, czytać artykuły i rozwiązywać interaktywne zadania. Internet oferuje wiele darmowych materiałów, które mogą pomóc w zrozumieniu geometrii.

Podsumowanie

Trapez równoramienny, choć na początku może wydawać się skomplikowany, to figura geometryczna, którą można zrozumieć i opanować. Kluczem jest zrozumienie jego właściwości i umiejętność wykorzystywania ich do rozwiązywania zadań. Pamiętaj, że wiedza o geometrii ma swoje zastosowania w realnym świecie i rozwija umiejętność logicznego myślenia.

Czy czujesz się teraz pewniej w obliczaniu kątów w trapezie równoramiennym? Jakie zadanie chciałbyś rozwiązać jako następne?