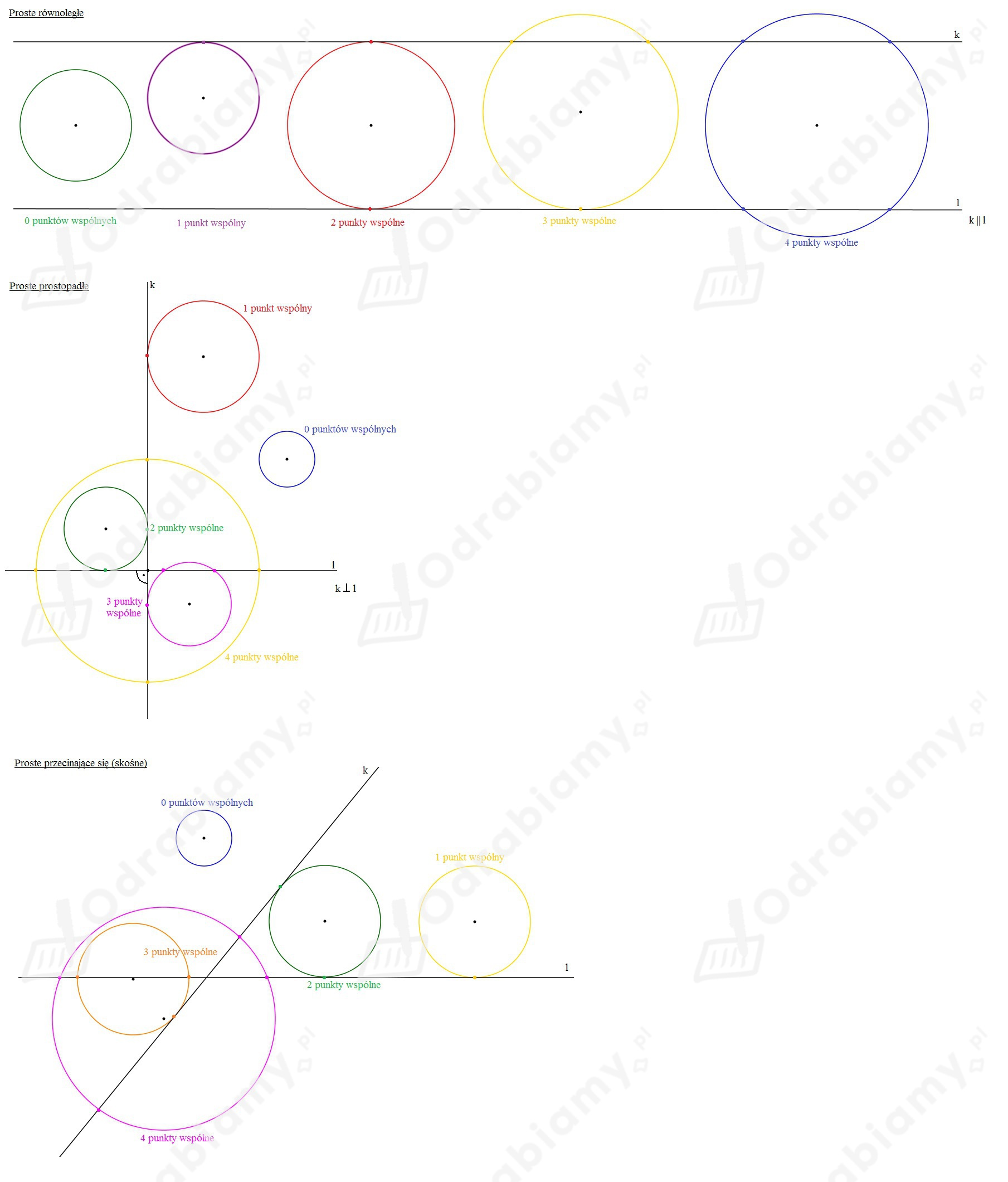
Ile Punktów Wspólnych Z Osiami Układu Współrzędnych Ma Okrąg

Okrąg w układzie współrzędnych to nic innego jak zbiór punktów, które są w tej samej odległości od jednego konkretnego punktu, zwanego środkiem okręgu. Ta stała odległość to promień okręgu. Ale jak to się przekłada na punkty wspólne z osiami układu współrzędnych, czyli osią X i osią Y? Spójrzmy na to krok po kroku.

Mówiąc najprościej, punkty wspólne okręgu z osiami to te miejsca, w których okrąg przecina oś X lub oś Y. Może przecinać, a może tylko dotykać, a może w ogóle nie mieć punktów wspólnych – to zależy od położenia środka okręgu i długości jego promienia.

Okrąg opisuje równanie: (x - a)² + (y - b)² = r², gdzie (a, b) to współrzędne środka okręgu, a r to promień. To równanie mówi nam wszystko, co musimy wiedzieć o okręgu.

Żeby znaleźć punkty przecięcia z osią X, musimy w równaniu okręgu podstawić y = 0. Dlaczego? Bo na osi X wszystkie punkty mają współrzędną y równą zero. Więc podstawiając y = 0 do równania okręgu, dostaniemy równanie, które pozwoli nam znaleźć x-owe współrzędne punktów przecięcia okręgu z osią X.

Otrzymujemy wtedy: (x - a)² + (0 - b)² = r², co upraszcza się do (x - a)² + b² = r². Teraz musimy rozwiązać to równanie ze względu na x. Przenosimy b² na drugą stronę równania: (x - a)² = r² - b².

Teraz musimy spierwiastkować obie strony równania. Pamiętajmy, że pierwiastek kwadratowy może dać wynik dodatni lub ujemny. Dostajemy więc: x - a = ±√(r² - b²).

Przenosimy a na drugą stronę: x = a ±√(r² - b²).

Teraz musimy przeanalizować, co ten wzór oznacza. Mamy tutaj trzy możliwości:

r² - b² > 0: W takim przypadku √(r² - b²) to liczba rzeczywista, większa od zera. Mamy dwa różne rozwiązania dla x: x₁ = a + √(r² - b²) oraz x₂ = a - √(r² - b²). Oznacza to, że okrąg przecina oś X w dwóch różnych punktach. Współrzędne tych punktów to (x₁, 0) i (x₂, 0).
r² - b² = 0: W tym przypadku √(r² - b²) = 0. Mamy tylko jedno rozwiązanie dla x: x = a. Oznacza to, że okrąg dotyka osi X w jednym punkcie. Współrzędne tego punktu to (a, 0). Mówimy wtedy, że oś X jest styczna do okręgu.
r² - b² < 0: W tym przypadku √(r² - b²) nie jest liczbą rzeczywistą (jest liczbą zespoloną). Oznacza to, że równanie nie ma rozwiązań w zbiorze liczb rzeczywistych. Oznacza to, że okrąg nie przecina ani nie dotyka osi X. Nie ma żadnych punktów wspólnych.

Analogicznie postępujemy, żeby znaleźć punkty przecięcia okręgu z osią Y. Tym razem podstawiamy x = 0 do równania okręgu. Dlaczego? Bo na osi Y wszystkie punkty mają współrzędną x równą zero.

Otrzymujemy: (0 - a)² + (y - b)² = r², co upraszcza się do a² + (y - b)² = r². Przenosimy a² na drugą stronę: (y - b)² = r² - a².

Pierwiastkujemy obie strony: y - b = ±√(r² - a²).

Przenosimy b na drugą stronę: y = b ±√(r² - a²).

I znowu, analizujemy trzy możliwości:

r² - a² > 0: Mamy dwa różne rozwiązania dla y: y₁ = b + √(r² - a²) oraz y₂ = b - √(r² - a²). Oznacza to, że okrąg przecina oś Y w dwóch różnych punktach. Współrzędne tych punktów to (0, y₁) i (0, y₂).
r² - a² = 0: Mamy tylko jedno rozwiązanie dla y: y = b. Oznacza to, że okrąg dotyka osi Y w jednym punkcie. Współrzędne tego punktu to (0, b). Oś Y jest styczna do okręgu.
r² - a² < 0: Równanie nie ma rozwiązań rzeczywistych. Okrąg nie przecina ani nie dotyka osi Y.

Ile punktów wspólnych może mieć okrąg z osiami?

Podsumowując, okrąg może mieć od zera do dwóch punktów wspólnych z osią X, oraz od zera do dwóch punktów wspólnych z osią Y. Łącznie, okrąg może mieć od 0 do 4 punktów wspólnych z obiema osiami układu współrzędnych. Wszystko zależy od położenia środka okręgu (czyli wartości a i b) oraz od długości promienia r.

Możemy to sobie wyobrazić. Jeśli okrąg jest bardzo mały i leży daleko od obu osi, to nie będzie miał żadnych punktów wspólnych. Jeśli okrąg jest większy i jego środek leży blisko osi, to może przeciąć jedną oś w dwóch punktach, a drugą wcale. Jeśli okrąg jest duży i jego środek leży blisko początku układu współrzędnych, to może przeciąć obie osie w dwóch punktach.

Żeby dokładnie określić liczbę punktów wspólnych, musimy znać współrzędne środka okręgu i promień. Potem, korzystając z powyższych wzorów, możemy sprawdzić, ile rozwiązań mają nasze równania. Pamiętajmy, że to, czy okrąg przecina oś, dotyka jej, czy nie ma z nią punktów wspólnych, zależy od znaku wyrażenia pod pierwiastkiem (r² - b² dla osi X i r² - a² dla osi Y).

Przeanalizujmy kilka przykładów:

Okrąg o równaniu (x - 2)² + (y - 3)² = 1: W tym przypadku a = 2, b = 3, r = 1.
- Dla osi X: r² - b² = 1² - 3² = 1 - 9 = -8 < 0. Brak punktów wspólnych z osią X.
- Dla osi Y: r² - a² = 1² - 2² = 1 - 4 = -3 < 0. Brak punktów wspólnych z osią Y. Okrąg nie ma żadnych punktów wspólnych z osiami.
Okrąg o równaniu (x - 1)² + (y - 0)² = 1: W tym przypadku a = 1, b = 0, r = 1.
- Dla osi X: r² - b² = 1² - 0² = 1 > 0. Dwa punkty wspólne z osią X. x = 1 ± √1 = 1 ± 1. Czyli x₁ = 2, x₂ = 0. Punkty wspólne to (2, 0) i (0, 0).
- Dla osi Y: r² - a² = 1² - 1² = 0. Jeden punkt wspólny z osią Y. y = 0 ± √0 = 0. Punkt wspólny to (0, 0). Okrąg ma trzy punkty wspólne z osiami: (2, 0) i (0, 0). Punkt (0,0) został policzony dwukrotnie, raz dla osi X i raz dla osi Y.
Okrąg o równaniu (x - 0)² + (y - 0)² = 4: W tym przypadku a = 0, b = 0, r = 2.
- Dla osi X: r² - b² = 4 - 0 = 4 > 0. Dwa punkty wspólne z osią X. x = 0 ± √4 = ±2. Punkty wspólne to (2, 0) i (-2, 0).
- Dla osi Y: r² - a² = 4 - 0 = 4 > 0. Dwa punkty wspólne z osią Y. y = 0 ± √4 = ±2. Punkty wspólne to (0, 2) i (0, -2). Okrąg ma cztery punkty wspólne z osiami: (2, 0), (-2, 0), (0, 2), (0, -2).

Pamiętajcie, żeby zawsze dokładnie analizować równanie okręgu i zwracać uwagę na znaki, żeby poprawnie określić liczbę punktów wspólnych z osiami układu współrzędnych.