Ile Osi Symetrii Ma Prosta

Czy kiedykolwiek zastanawiałeś się, dlaczego niektóre obiekty wydają się tak przyjemne dla oka? Często kluczem jest symetria. A jednym z jej najbardziej podstawowych i fascynujących rodzajów jest symetria osiowa, czyli ile osi symetrii ma prosta. Ten artykuł skierowany jest do wszystkich entuzjastów matematyki, uczniów, studentów i każdego, kto jest ciekawy świata, który nas otacza. Przyjrzymy się bliżej temu zjawisku, wyjaśniając je w prosty i zrozumiały sposób. Gotowi na podróż do świata idealnego porządku?

Co to jest symetria osiowa?

Zanim przejdziemy do sedna sprawy, musimy zrozumieć, czym właściwie jest symetria osiowa. Wyobraź sobie, że masz rysunek i linię. Jeżeli po "złożeniu" rysunku wzdłuż tej linii, obie połówki idealnie się pokrywają, to mówimy o symetrii osiowej. Ta linia to oś symetrii.

Definicja formalna

Matematycznie, symetria osiowa (lub odbicie osiowe) względem prostej l to przekształcenie geometryczne, które każdemu punktowi P przypisuje punkt P' taki, że:

• Odcinek PP' jest prostopadły do prostej l.
• Punkt przecięcia odcinka PP' z prostą l jest środkiem odcinka PP'.

Innymi słowy, prosta l jest symetralną odcinka PP'.

Przykłady z życia codziennego

Symetrię osiową widzimy wszędzie wokół nas. Spójrz na:

• Motyle: Ich skrzydła są niemal idealnym przykładem symetrii osiowej.
• Liście: Większość liści ma wyraźną oś symetrii przebiegającą przez ich środek.
• Twarz ludzka: Choć nie jesteśmy doskonale symetryczni, to przybliżenie osi symetrii można znaleźć przez środek twarzy.

Te naturalne przykłady pokazują, jak wszechobecna jest symetria w naszym otoczeniu.

Prosta i jej osie symetrii

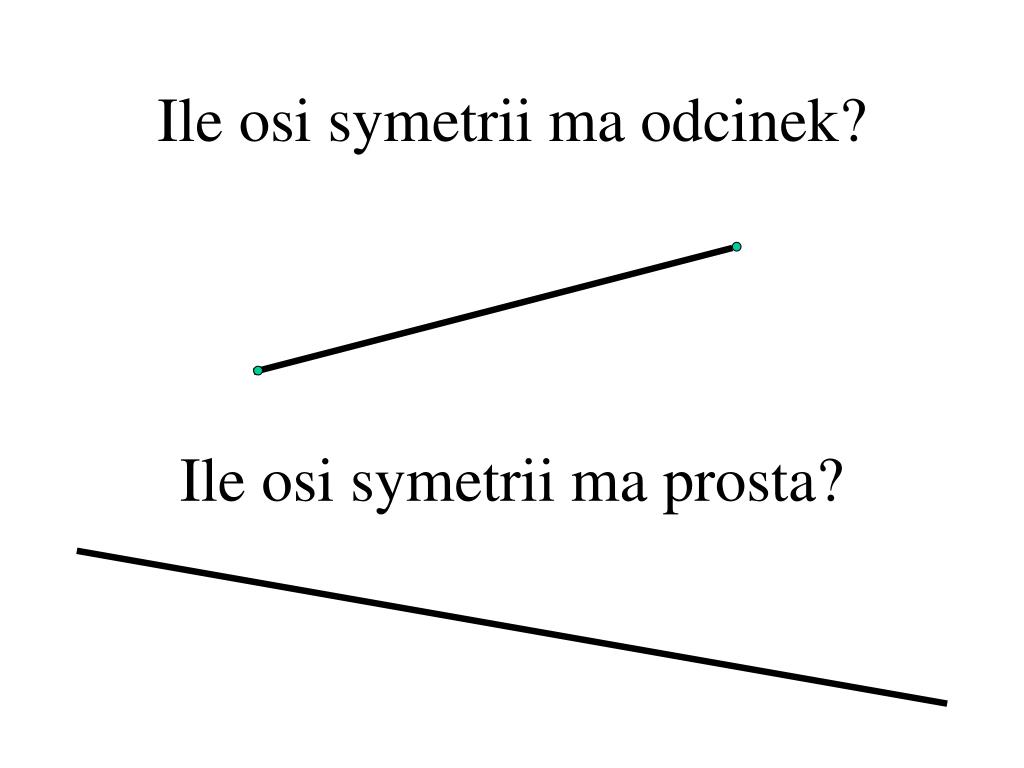
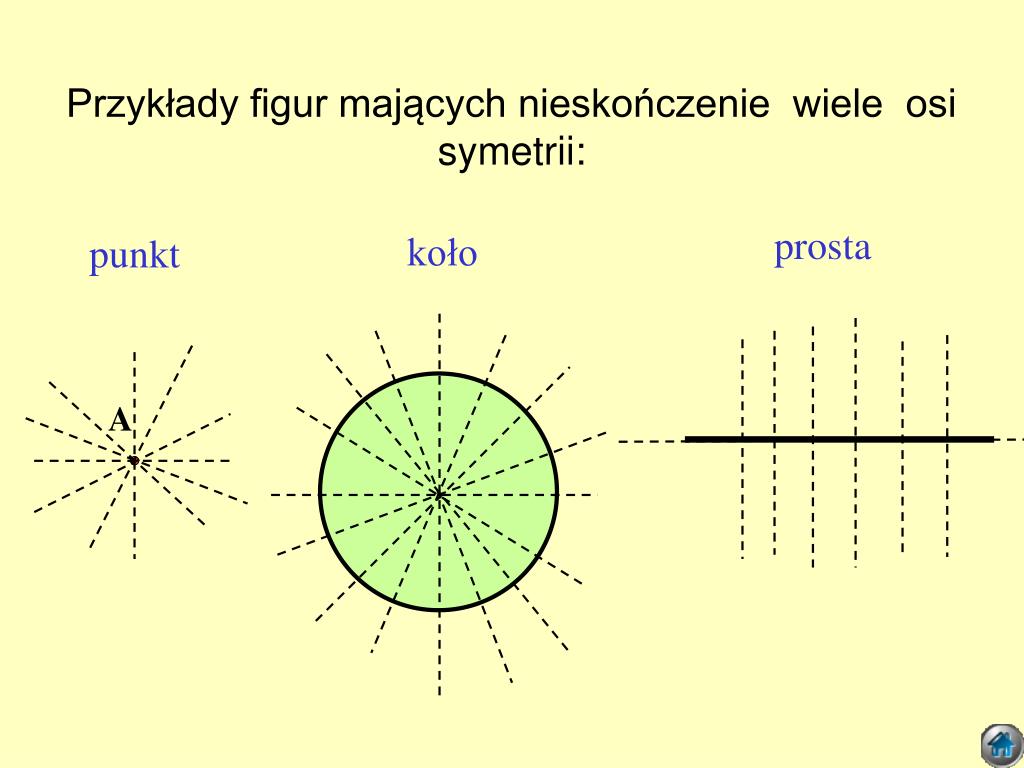
Teraz dochodzimy do kluczowego pytania: ile osi symetrii ma prosta? Odpowiedź może zaskoczyć, ale prosta ma nieskończenie wiele osi symetrii!

Dlaczego tak jest?

Zastanówmy się. Aby linia była osią symetrii, "złożenie" figury wzdłuż niej musi dawać identyczny obraz po obu stronach. Dla prostej, każda prosta prostopadła do niej jest osią symetrii. Ponadto, sama prosta też jest swoją osią symetrii (bo "złożenie" jej na samej sobie daje identyczny obraz).

Dowód geometryczny

Wyobraźmy sobie prostą k. Możemy przeprowadzić przez nią nieskończenie wiele prostych l, które są do niej prostopadłe. Dla każdej takiej prostej l, odbicie prostej k względem l da nam tę samą prostą k. Oznacza to, że każda z tych prostych l jest osią symetrii prostej k. Dodatkowo, sama prosta k również jest swoją osią symetrii. Stąd, prosta ma nieskończenie wiele osi symetrii.

Wyobraźnia przestrzenna

Pomyśl o tym tak: wyobraź sobie linię narysowaną na kartce. Możesz złożyć kartkę na pół wzdłuż tej linii – to jedna oś symetrii. Ale możesz też złożyć kartkę na pół wzdłuż *dowolnej* linii, która przecina pierwszą linię pod kątem prostym. Zawsze otrzymasz identyczny obraz po obu stronach. A takich linii przecinających pod kątem prostym jest nieskończenie wiele!

Porównanie z innymi figurami geometrycznymi

Warto porównać ilość osi symetrii prostej z innymi figurami geometrycznymi, aby lepiej zrozumieć to pojęcie:

• Odcinek: Ma dwie osie symetrii: symetralną odcinka i prostą, na której leży odcinek.
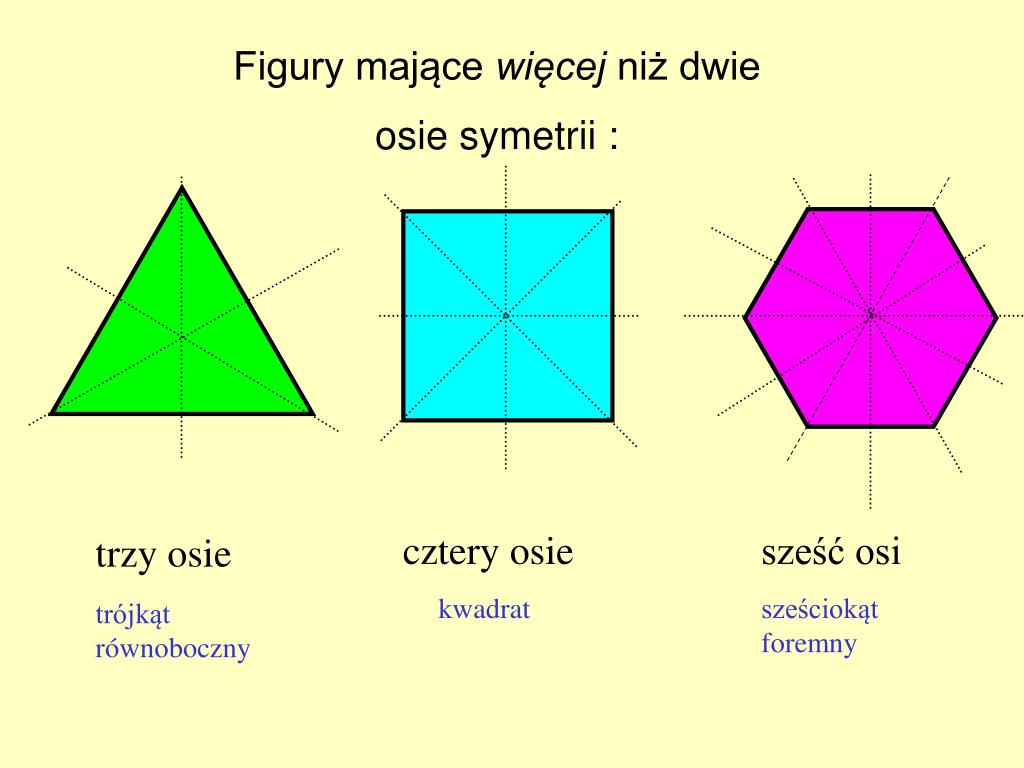
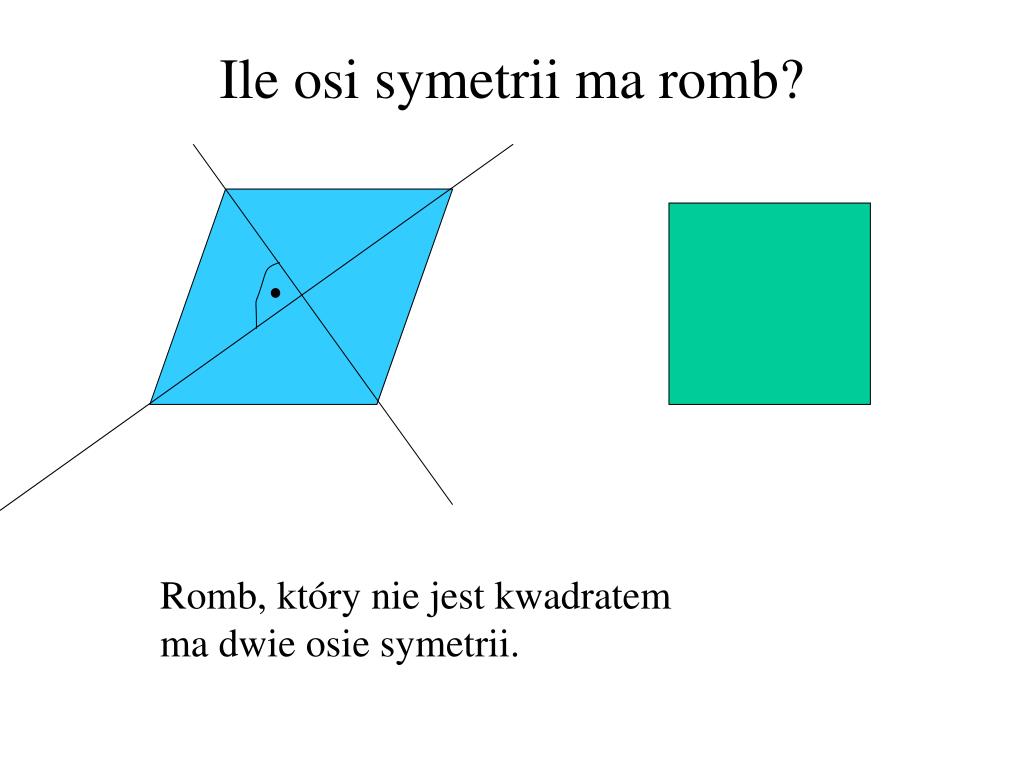
• Kwadrat: Ma cztery osie symetrii: dwie przechodzące przez środki przeciwległych boków i dwie przechodzące przez wierzchołki.
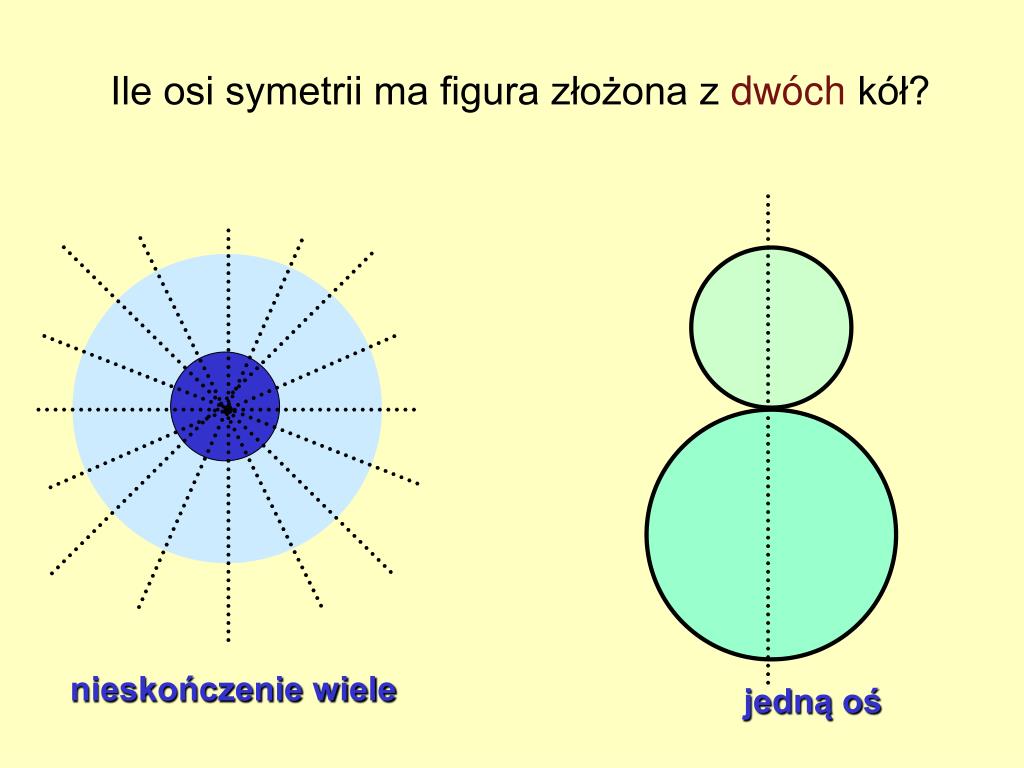
• Okrąg: Ma nieskończenie wiele osi symetrii – każda prosta przechodząca przez środek okręgu.

Widzimy więc, że prosta, podobnie jak okrąg, wyróżnia się nieskończoną liczbą osi symetrii. Jest to związane z jej nieograniczoną naturą.

Zastosowania symetrii osiowej

Symetria osiowa, choć wydaje się abstrakcyjna, ma wiele praktycznych zastosowań w różnych dziedzinach:

• Architektura: Symetria jest często wykorzystywana w projektowaniu budynków, nadając im harmonię i estetykę. Przykładem są fasady budynków, które często są symetryczne względem osi pionowej.
• Sztuka i wzornictwo: Symetria jest powszechnie stosowana w sztuce i wzornictwie, tworząc przyjemne dla oka kompozycje. Wzory na tkaninach, witraże, mandale – to tylko niektóre przykłady.
• Fizyka: Zasady symetrii odgrywają kluczową rolę w fizyce, zwłaszcza w teoriach cząstek elementarnych. Na przykład, symetria CPT (ładunku, parzystości i czasu) jest fundamentalną symetrią w Modelu Standardowym.
• Informatyka: Algorytmy grafiki komputerowej często wykorzystują symetrię osiową do tworzenia odbić lustrzanych i generowania symetrycznych obrazów.

Zrozumienie symetrii osiowej pozwala nam docenić piękno i porządek w otaczającym nas świecie, a także wykorzystywać ją w praktyczny sposób w różnych dziedzinach.

Podsumowanie

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, dlaczego prosta ma nieskończenie wiele osi symetrii. Pamiętaj, że każda prosta prostopadła do danej prostej, jak również sama ta prosta, jest jej osią symetrii. To fascynujący przykład tego, jak proste pojęcia matematyczne mogą prowadzić do zaskakujących wniosków. Zachęcam Cię do dalszego zgłębiania tajników geometrii i poszukiwania symetrii w swoim otoczeniu. Odkrywanie piękna matematyki może być niezwykle satysfakcjonujące!

Dzięki za przeczytanie! Mam nadzieję, że dowiedziałeś/dowiedziałaś się czegoś nowego i interesującego. Pamiętaj, matematyka jest wszędzie wokół nas – wystarczy tylko otworzyć oczy i zacząć obserwować!