Ile Krawędzi Ma Graniastosłup Pięciokątny

Zastanawiałeś się kiedyś, ile krawędzi ma graniastosłup pięciokątny? Na pierwszy rzut oka to może wydawać się skomplikowane, ale tak naprawdę z odrobiną wiedzy i cierpliwości, każdy może to zrozumieć. Wiele osób ma problem z wyobrażeniem sobie figur przestrzennych i policzeniem ich elementów, zwłaszcza bez fizycznego modelu. Ten artykuł ma na celu uprościć to zagadnienie i pomóc Ci raz na zawsze zapamiętać, jak obliczyć liczbę krawędzi w graniastosłupie pięciokątnym, a przy okazji w innych graniastosłupach również.

Wyobraź sobie, że jesteś uczniem, który musi zdać egzamin z geometrii przestrzennej. Albo, że pracujesz w firmie architektonicznej i potrzebujesz precyzyjnie obliczyć zużycie materiałów na budowę nietypowej konstrukcji. Zrozumienie podstaw geometrii przestrzennej, takich jak liczba krawędzi w graniastosłupie, jest kluczowe. Błędne obliczenia mogą prowadzić do problemów na wielu płaszczyznach – od kiepskich ocen po straty finansowe.

Czym jest graniastosłup?

Zanim przejdziemy do krawędzi graniastosłupa pięciokątnego, przypomnijmy sobie, czym w ogóle jest graniastosłup. Graniastosłup to bryła, która ma dwie identyczne i równoległe podstawy, połączone ścianami bocznymi będącymi równoległobokami (najczęściej prostokątami). Możemy wyróżnić graniastosłupy proste (ściany boczne są prostopadłe do podstaw) i pochyłe. W naszym przypadku skupimy się na graniastosłupach prostych, ponieważ są najczęściej spotykane i najłatwiejsze do zrozumienia.

Podstawą graniastosłupa może być dowolny wielokąt. Nazwa graniastosłupa pochodzi od kształtu jego podstawy. Na przykład:

Graniastosłup trójkątny: podstawą jest trójkąt.
Graniastosłup czworokątny: podstawą jest czworokąt (np. kwadrat, prostokąt, trapez).
Graniastosłup pięciokątny: podstawą jest pięciokąt.
Graniastosłup sześciokątny: podstawą jest sześciokąt.

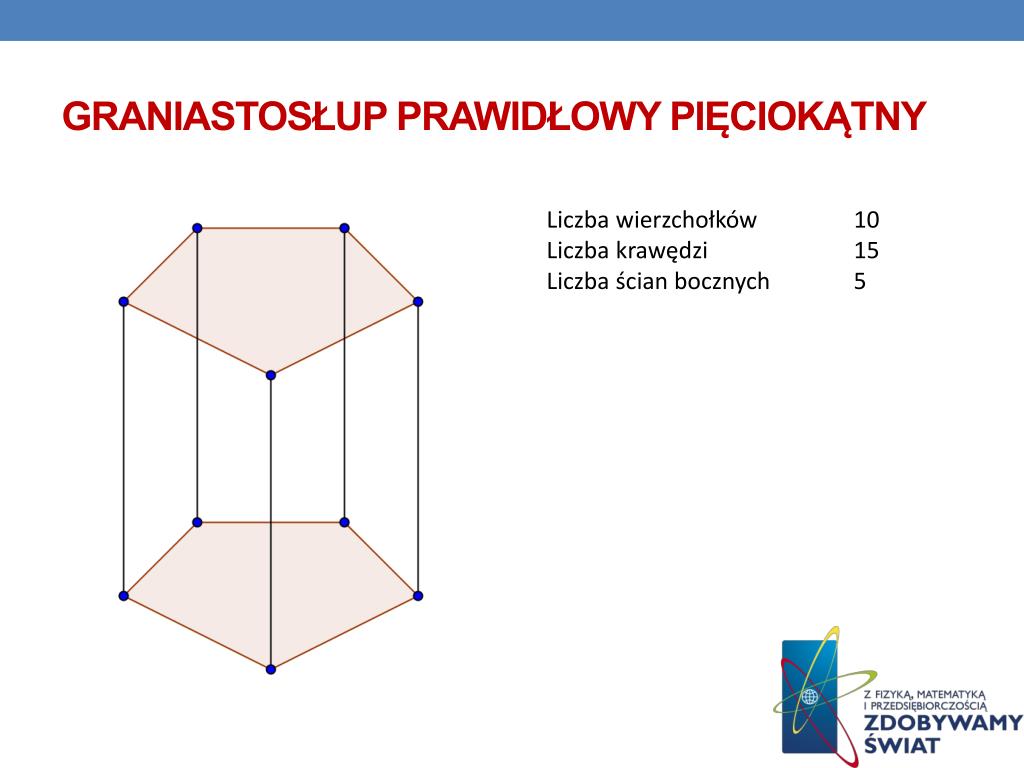
Graniastosłup pięciokątny – wizualizacja

Wyobraź sobie dwa identyczne pięciokąty, które leżą równolegle do siebie. Następnie, połącz każdy wierzchołek jednego pięciokąta z odpowiadającym mu wierzchołkiem drugiego pięciokąta za pomocą linii prostych. Te proste linie to krawędzie boczne, a pięciokąty to podstawy. W ten sposób powstaje graniastosłup pięciokątny.

Jak obliczyć liczbę krawędzi graniastosłupa pięciokątnego?

Istnieją dwa sposoby, aby to zrobić:

Sposób 1: Zrozumienie struktury

Graniastosłup pięciokątny składa się z:

Dwu podstaw: każda z nich jest pięciokątem, więc ma 5 krawędzi. Czyli łącznie 2 * 5 = 10 krawędzi podstaw.
Pięciu ścian bocznych: każda z nich jest prostokątem, a każdy prostokąt ma 4 krawędzie. Ale! Dwie z tych krawędzi należą już do podstaw. Zatem każda ściana boczna "dodaje" jedną krawędź. A mamy 5 takich ścian, czyli 5 krawędzi bocznych.

Sumując krawędzie podstaw i krawędzie boczne: 10 + 5 = 15 krawędzi. To jest błąd! Nie możemy liczyć ścian bocznych w ten sposób, ponieważ liczymy krawędzie podstaw podwójnie. Musimy policzyć je inaczej.

Prawidłowe rozumowanie:

Dwie podstawy, każda z 5 krawędziami: 2 * 5 = 10 krawędzi
Pięć krawędzi łączących wierzchołki podstaw (krawędzie boczne): 5 krawędzi

Zatem: 10 + 5 = 15 krawędzi. Nadal błąd! Już wiemy, że odpowiedź jest 15. Gdzie leży problem? Spróbujmy z innym podejściem.

Sposób 2: Użycie wzoru

Istnieje ogólny wzór na liczbę krawędzi w graniastosłupie:

Liczba krawędzi = 3 * n

Gdzie 'n' to liczba boków wielokąta w podstawie. W przypadku graniastosłupa pięciokątnego, n = 5.

Zatem, liczba krawędzi = 3 * 5 = 15

Gratulacje! Udało nam się dojść do prawidłowego wyniku.

Dlaczego to działa?

Ten wzór działa, ponieważ:

Każda z dwóch podstaw ma 'n' krawędzi.
Jest 'n' krawędzi bocznych łączących wierzchołki podstaw.

W sumie: n + n + n = 3n

Przykłady innych graniastosłupów

Sprawdźmy, czy wzór działa dla innych graniastosłupów:

Graniastosłup trójkątny: n = 3, liczba krawędzi = 3 * 3 = 9
Graniastosłup czworokątny (np. prostopadłościan): n = 4, liczba krawędzi = 3 * 4 = 12
Graniastosłup sześciokątny: n = 6, liczba krawędzi = 3 * 6 = 18

Wszystko się zgadza!

Potencjalne trudności i jak je pokonać

Jedną z trudności może być pomylenie graniastosłupa z ostrosłupem. Ostrosłup ma tylko jedną podstawę i wierzchołek, do którego zbiegają się wszystkie ściany boczne. Graniastosłup ma dwie podstawy i równoległe ściany boczne.

Innym problemem może być liczenie krawędzi na rysunku. Często niektóre krawędzie są ukryte za bryłą i trudno je zobaczyć. Najlepiej wtedy wyobrazić sobie bryłę w przestrzeni lub, jeszcze lepiej, zbudować model!

Czasami uczniowie zapominają wzoru. W takiej sytuacji warto przypomnieć sobie, jak zbudowany jest graniastosłup i policzyć krawędzie krok po kroku.

Realne zastosowania

Zrozumienie geometrii przestrzennej, w tym liczenie krawędzi graniastosłupów, ma wiele praktycznych zastosowań:

Architektura: Obliczanie zużycia materiałów, projektowanie konstrukcji.
Inżynieria: Projektowanie maszyn i urządzeń, analiza wytrzymałości konstrukcji.
Grafika komputerowa: Tworzenie modeli 3D, animacje.
Stolarstwo: Projektowanie i budowa mebli.

Wyobraź sobie projektowanie nowego wieżowca o podstawie pięciokątnej. Dokładne obliczenie liczby krawędzi, wierzchołków i ścian jest niezbędne do zapewnienia stabilności i bezpieczeństwa konstrukcji.

Kontrargumenty i ich obalanie

Można spotkać się z opinią, że geometria przestrzenna jest trudna i nieprzydatna w życiu codziennym. Jest to błędne przekonanie. Geometria przestrzenna rozwija wyobraźnię przestrzenną, umiejętność logicznego myślenia i rozwiązywania problemów. Umiejętności te są przydatne w wielu dziedzinach życia, zarówno zawodowego, jak i prywatnego.

Ktoś może powiedzieć, że wystarczy użyć kalkulatora online do obliczenia liczby krawędzi. Owszem, kalkulator może pomóc, ale zrozumienie podstawowych zasad geometrii jest niezbędne, aby móc prawidłowo interpretować wyniki i unikać błędów.

Podsumowanie i dalsze kroki

Podsumowując, graniastosłup pięciokątny ma 15 krawędzi. Możemy to obliczyć na dwa sposoby: analizując strukturę bryły lub używając wzoru 3 * n. Zrozumienie geometrii przestrzennej jest ważne dla wielu dziedzin życia.

Teraz, gdy znasz odpowiedź na to pytanie, spróbuj odpowiedzieć na inne: Ile wierzchołków ma graniastosłup pięciokątny? Albo ścian? Spróbuj samodzielnie narysować graniastosłup pięciokątny i policzyć jego elementy. Powodzenia!

Jeśli chcesz pogłębić swoją wiedzę z zakresu geometrii przestrzennej, poszukaj dodatkowych materiałów edukacyjnych, takich jak książki, kursy online lub filmy instruktażowe. Praktyka czyni mistrza!