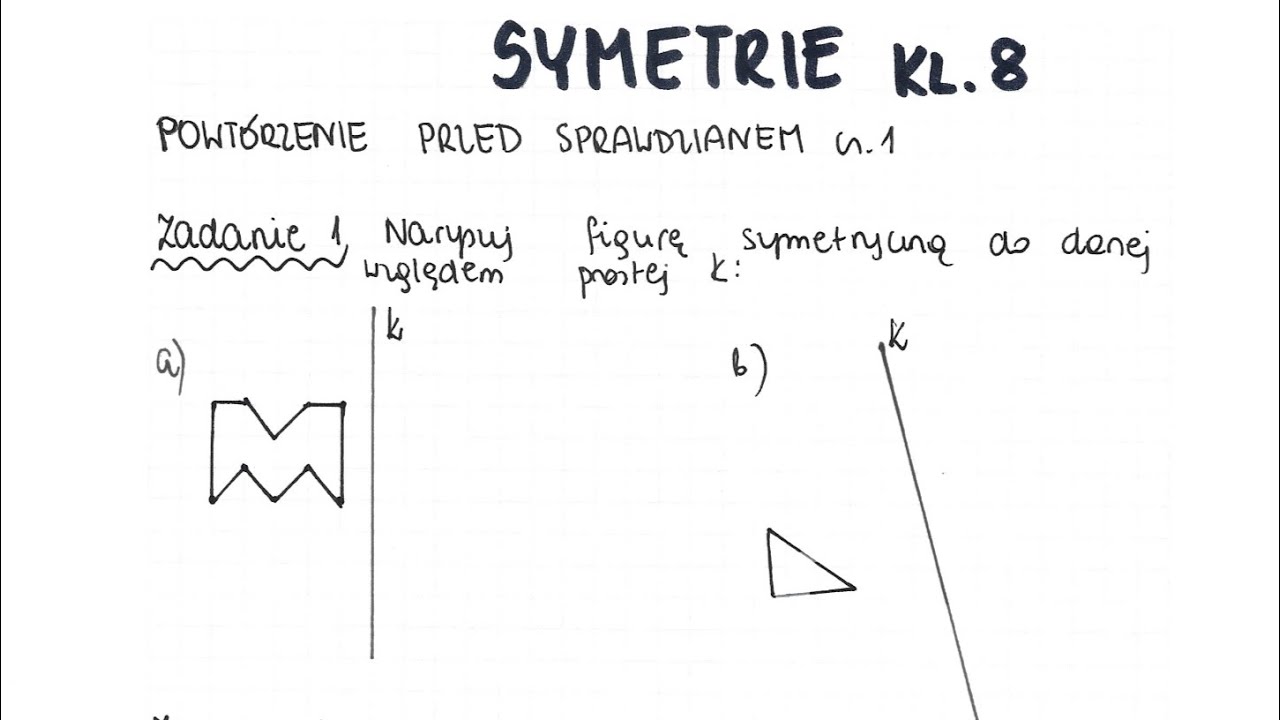
Gwo Sprawdzian Matematyka 1 Gimnazjum Symetrie

Czy matematyka musi być nudna? Absolutnie nie! Szczególnie, gdy mówimy o symetriach – fascynującym zagadnieniu, które możesz spotkać już w 1. klasie gimnazjum, na przykład w sprawdzianie z wydawnictwa GWO. Ten artykuł jest dla Ciebie, uczniu pierwszej klasy, który chce zrozumieć symetrie, by błyszczeć na sprawdzianie i czerpać radość z matematyki. Odkryjemy, że symetrie są wszędzie wokół nas, a ich zrozumienie otwiera drzwi do fascynującego świata geometrii.

Co to w ogóle jest symetria?

Symetria to, najprościej mówiąc, harmonia i równowaga w kształcie. Wyobraź sobie motyla – jego lewe skrzydło jest prawie idealnym odbiciem prawego. To właśnie jest przykład symetrii.

W matematyce, szczególnie w geometrii, wyróżniamy kilka podstawowych rodzajów symetrii:

• Symetria osiowa: Tak, jak odbicie w lustrze! Masz oś symetrii – prostą, względem której figura wygląda identycznie po "przerzuceniu".
• Symetria środkowa: Wyobraź sobie punkt, względem którego figura obraca się o 180 stopni i nadal wygląda tak samo. Ten punkt to środek symetrii.

Symetria osiowa – zwierciadlane odbicie

Jak rozpoznać symetrię osiową?

Figura ma symetrię osiową, jeśli istnieje prosta (oś symetrii), która dzieli ją na dwie identyczne połówki, które są swoimi odbiciami lustrzanymi.

Przykład: Litera "A" (duża) ma symetrię osiową. Oś symetrii przebiega pionowo przez środek litery.

Jak rysować symetrię osiową?

Rysowanie figury symetrycznej osiowo wymaga trochę wprawy, ale to nic trudnego! Możesz skorzystać z następujących wskazówek:

1. Narysuj oś symetrii (prostą).
2. Wybierz kilka charakterystycznych punktów na figurze, którą chcesz odbić.
3. Zmierz odległość każdego punktu od osi symetrii.
4. Odmierz tę samą odległość po drugiej stronie osi i zaznacz punkt.
5. Połącz punkty, aby uzyskać odbicie figury.

Symetria środkowa – obrót o 180 stopni

Jak rozpoznać symetrię środkową?

Figura ma symetrię środkową, jeśli istnieje punkt (środek symetrii), wokół którego można ją obrócić o 180 stopni, a figura pozostanie niezmieniona.

Przykład: Litera "S" ma symetrię środkową. Punkt w środku litery jest jej środkiem symetrii.

Jak rysować symetrię środkową?

Rysowanie figury symetrycznej środkowo również wymaga precyzji:

1. Zaznacz środek symetrii (punkt).
2. Wybierz kilka charakterystycznych punktów na figurze, którą chcesz odbić.
3. Poprowadź prostą przez każdy punkt i środek symetrii.
4. Odmierz odległość od punktu do środka symetrii.
5. Odmierz tę samą odległość po drugiej stronie środka symetrii i zaznacz punkt.
6. Połącz punkty, aby uzyskać odbicie figury.

Symetrie w życiu codziennym

Może Ci się wydawać, że symetrie to tylko teoria matematyczna, ale w rzeczywistości otaczają nas one każdego dnia. Zastanów się:

• Architektura: Wiele budynków projektuje się symetrycznie, aby uzyskać estetyczny wygląd. Na przykład, fasady wielu pałaców i kościołów są symetryczne osiowo.
• Natura: Jak już wspomnieliśmy, motyle, liście, kwiaty – wiele elementów przyrody charakteryzuje się symetrią.
• Sztuka: Artyści często wykorzystują symetrię, aby tworzyć harmonijne i przyjemne dla oka kompozycje.
• Przedmioty codziennego użytku: Zastanów się nad kształtem talerza, szklanki, czy nawet wideelca – często są symetryczne!

Symetrie na sprawdzianie z matematyki GWO

Na sprawdzianie z matematyki w 1. klasie gimnazjum, wydawnictwa GWO, możesz spodziewać się zadań, które sprawdzają Twoją wiedzę na temat:

• Rozpoznawania figur symetrycznych osiowo i środkowo.
• Rysowania figur symetrycznych.
• Określania osi symetrii i środków symetrii.
• Zastosowania wiedzy o symetriach w rozwiązywaniu problemów geometrycznych.

Wskazówka: Zwróć szczególną uwagę na dokładność rysunków. Używaj linijki i ołówka, aby precyzyjnie odmierzać odległości i rysować proste.

Pamiętaj!

Zrozumienie symetrii to nie tylko klucz do sukcesu na sprawdzianie, ale również sposób na lepsze rozumienie świata wokół nas. Obserwuj otoczenie, szukaj symetrii w architekturze, naturze i sztuce. Ćwicz rysowanie figur symetrycznych – to pomoże Ci utrwalić wiedzę i rozwinąć wyobraźnię przestrzenną. Powodzenia na sprawdzianie!

Matematyka może być fascynująca! Odkryj to sam!