Graniastoslupy Zadania Klasa 8 Gwo Pdf

Witaj ósmoklasisto! Przygotuj się na fascynującą podróż do świata graniastosłupów. Często spotykamy je w życiu codziennym, choć możemy nie zdawać sobie z tego sprawy. W tym artykule, zamiast suchych definicji, użyjemy wyobraźni i przykładów, by zrozumieć, czym naprawdę są te figury.

Co to właściwie jest graniastosłup?

Wyobraź sobie pudełko. Zwykłe, kartonowe pudełko. To najprostszy przykład graniastosłupa! A dokładniej – graniastosłupa prostego. Ale zanim przejdziemy do szczegółów, zdefiniujmy, co to w ogóle jest.

Graniastosłup to bryła, która ma dwie identyczne, równoległe podstawy (wspomniane "wieczka" pudełka) i ściany boczne, które są równoległobokami. Co ważne, te ściany boczne łączą odpowiednie wierzchołki podstaw. Brzmi skomplikowanie? Spokojnie, rozłóżmy to na czynniki pierwsze.

Podstawy

Podstawy mogą mieć różne kształty: trójkąt, kwadrat, pięciokąt, a nawet bardziej skomplikowany wielokąt. Wyobraź sobie, że masz foremkę do ciasteczek w kształcie serca. Układasz jeden kawałek ciasta (podstawa), a potem dokładnie taki sam kawałek na górze (druga podstawa). To właśnie te identyczne "ciasteczka" są podstawami graniastosłupa.

Ściany boczne

Ściany boczne to prostokąty lub równoległoboki, które łączą krawędzie podstaw. Wyobraź sobie kartkę papieru, którą owijasz dookoła foremek. Ta kartka tworzy ściany boczne. Jeśli foremki są ustawione prosto jedna nad drugą, to ściany boczne są prostokątami. Jeśli jednak jedna foremka jest lekko przesunięta względem drugiej, to ściany boczne stają się równoległobokami (ale nadal łączą odpowiadające sobie krawędzie podstaw).

Rodzaje graniastosłupów

Graniastosłupy dzielimy na różne rodzaje, głównie ze względu na kształt podstawy i kąt nachylenia ścian bocznych.

Graniastosłup prosty

To nasz "pudełkowy" typ. W graniastosłupie prostym ściany boczne są prostokątami i są prostopadłe do podstaw. Wyobraź sobie budynek. Jeśli ściany budynku stoją idealnie pionowo, tworzą kąt prosty z ziemią (podstawą), to mamy do czynienia z graniastosłupem prostym.

Graniastosłup pochyły

W graniastosłupie pochyłym ściany boczne są równoległobokami i nie są prostopadłe do podstaw. Wyobraź sobie pochyloną wieżę w Pizie. Choć nie jest to idealny graniastosłup, to ilustruje ideę pochylenia ścian bocznych. Ściany nie stoją prosto, tylko są "przechylone" na bok.

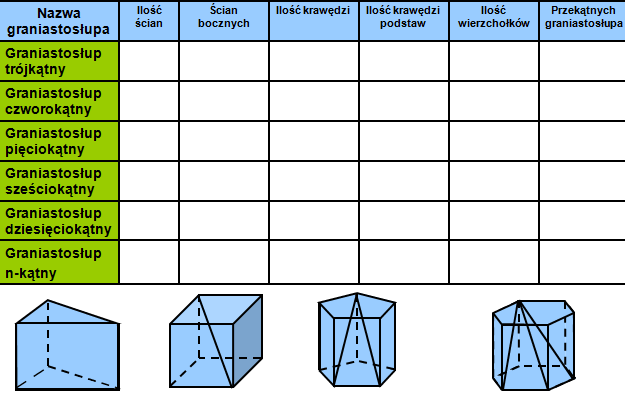
Graniastosłup trójkątny, czworokątny, pięciokątny...

Nazwa graniastosłupa zależy od kształtu podstawy. Jeśli podstawa jest trójkątem, mamy graniastosłup trójkątny. Jeśli kwadratem - graniastosłup czworokątny (który, jeśli jest prosty, nazywamy też prostopadłościanem lub sześcianem, jeśli wszystkie ściany są kwadratami). I tak dalej. Spójrz na dach domu - często ma kształt graniastosłupa trójkątnego.

Jak rozwiązywać zadania z graniastosłupami?

Typowe zadania dotyczą obliczania:

• Pola powierzchni: Suma pól wszystkich ścian (podstaw i ścian bocznych).
• Objętości: Iloczyn pola podstawy i wysokości graniastosłupa.

Kluczem do sukcesu jest zapamiętanie wzorów i umiejętność rozpoznawania kształtu podstawy.

Pole powierzchni całkowitej

Pole powierzchni całkowitej (Pc) graniastosłupa to suma pól dwóch podstaw (Pp) i pola powierzchni bocznej (Pb):

Pc = 2Pp + Pb

Pamiętaj, że Pp zależy od kształtu podstawy. Dla trójkąta będzie to (a*h)/2, dla kwadratu a*a, itd.

Objętość

Objętość (V) graniastosłupa to iloczyn pola podstawy (Pp) i wysokości (H):

V = Pp * H

Wysokość (H) to odległość między podstawami. W graniastosłupie prostym, wysokość jest długością ściany bocznej (która jest prostopadła do podstaw).

Przykładowe zadanie

Załóżmy, że mamy graniastosłup prosty trójkątny. Podstawa to trójkąt prostokątny o bokach 3 cm, 4 cm i 5 cm. Wysokość graniastosłupa wynosi 10 cm. Oblicz pole powierzchni całkowitej i objętość.

1. Pole podstawy (Pp): Pp = (3 * 4) / 2 = 6 cm²
2. Pole powierzchni bocznej (Pb): Pb = (3 * 10) + (4 * 10) + (5 * 10) = 30 + 40 + 50 = 120 cm²
3. Pole powierzchni całkowitej (Pc): Pc = (2 * 6) + 120 = 12 + 120 = 132 cm²
4. Objętość (V): V = 6 * 10 = 60 cm³

Gdzie spotykamy graniastosłupy w życiu?

Graniastosłupy otaczają nas na każdym kroku!

• Budynki: Wiele budynków ma kształt graniastosłupów prostych.
• Czekolady Toblerone: Charakterystyczny kształt graniastosłupa trójkątnego.
• Pudełka: Różne rodzaje pudełek – od pudełek na buty po kartony transportowe.
• Kredki: Często mają kształt graniastosłupów sześciokątnych.

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, czym są graniastosłupy i jak rozwiązywać z nimi zadania. Pamiętaj – kluczem do sukcesu jest wizualizacja i praktyka. Powodzenia!