Graniastoslupy 8 Klasa Zadania Pdf

Cześć ósmoklasisto! Matematyka, a konkretnie geometria, potrafi czasem sprawić trudności. Szczególnie, kiedy w grę wchodzą graniastosłupy. Rozumiem doskonale, możesz czuć się przytłoczony wzorami, obliczeniami pól i objętości. Nie martw się, nie jesteś sam! Wielu uczniów w ósmej klasie boryka się z tym zagadnieniem.

Zanim przejdziemy do konkretnych zadań i PDF-ów, chcę cię uspokoić: graniastosłupy wcale nie są takie straszne, jak się wydają. Kluczem jest zrozumienie podstawowych pojęć i opanowanie kilku prostych wzorów. Pamiętaj, że praktyka czyni mistrza! Im więcej zadań rozwiążesz, tym pewniej się będziesz czuł.

Dlaczego Graniastosłupy Są Ważne?

Może się zastanawiasz, po co w ogóle uczyć się o graniastosłupach. Czy ta wiedza przyda mi się w życiu? Odpowiedź brzmi: tak! Geometria, w tym wiedza o graniastosłupach, rozwija myślenie przestrzenne, umiejętność rozwiązywania problemów i logicznego rozumowania. To umiejętności, które przydadzą się w wielu dziedzinach życia, nie tylko w szkole.

Wyobraź sobie architekta projektującego budynek – musi on doskonale znać właściwości geometryczne różnych brył, w tym graniastosłupów. Inżynier konstruujący most również potrzebuje tej wiedzy. Nawet w życiu codziennym, planując remont pokoju czy układając kafelki w łazience, korzystasz z podstaw geometrii.

A co z bardziej abstrakcyjnymi zastosowaniami? Programiści tworzący gry komputerowe wykorzystują geometrię do modelowania trójwymiarowych obiektów. Naukowcy analizujący struktury molekularne również potrzebują wiedzy o bryłach geometrycznych.

Co To Właściwie Jest Graniastosłup?

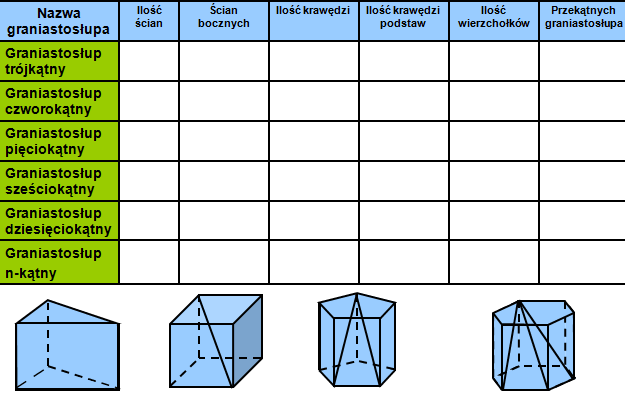
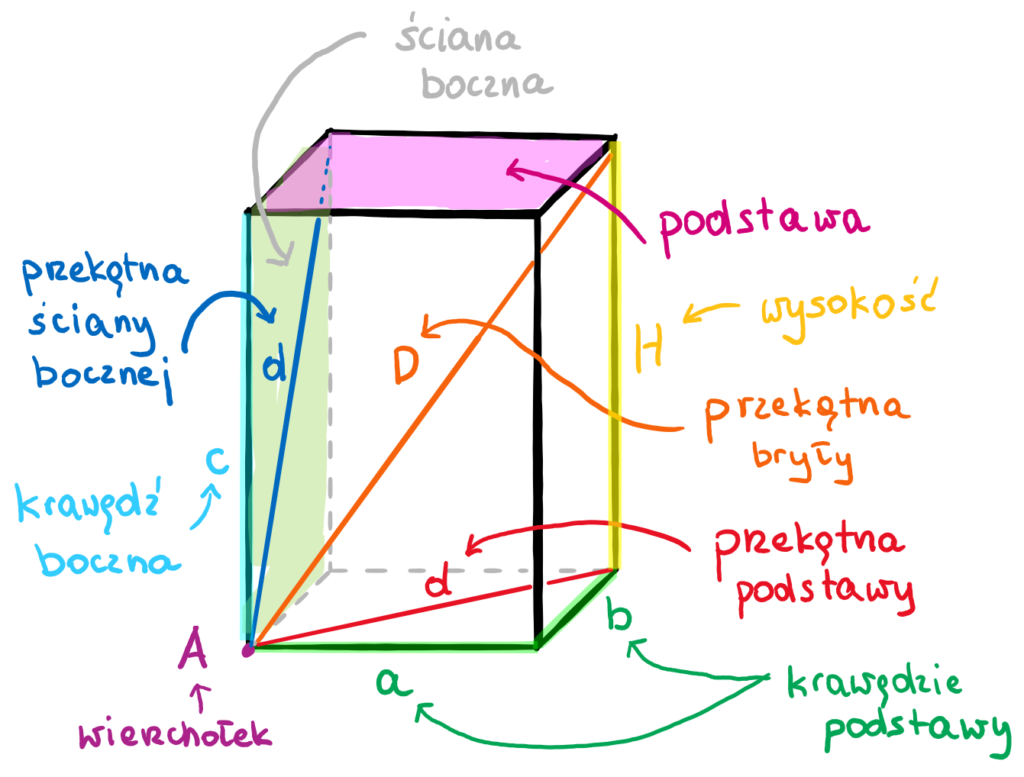
Zanim przejdziemy do zadań, przypomnijmy sobie, czym tak naprawdę jest graniastosłup. Graniastosłup to wielościan, który ma dwie identyczne i równoległe podstawy, będące wielokątami, oraz ściany boczne, które są równoległobokami.

Spróbuj sobie to wyobrazić:

Podstawy: Mogą to być trójkąty, kwadraty, prostokąty, pięciokąty, a nawet bardziej skomplikowane wielokąty. Ważne, żeby były identyczne i równoległe.
Ściany boczne: To prostokąty (w przypadku graniastosłupa prostego) lub równoległoboki (w przypadku graniastosłupa pochyłego).

Ze względu na kształt podstawy, graniastosłupy dzielimy na:

Graniastosłup trójkątny: Ma podstawę w kształcie trójkąta.
Graniastosłup czworokątny: Ma podstawę w kształcie czworokąta (np. kwadratu, prostokąta, trapezu).
Graniastosłup pięciokątny: Ma podstawę w kształcie pięciokąta.
I tak dalej...

Dodatkowo, rozróżniamy:

Graniastosłup prosty: Ściany boczne są prostopadłe do podstawy.
Graniastosłup pochyły: Ściany boczne nie są prostopadłe do podstawy.

Wzory, Które Musisz Znać

Do rozwiązywania zadań z graniastosłupów potrzebujesz znać kilka podstawowych wzorów:

Pole powierzchni całkowitej (Pc): Pc = 2 * Pp + Pb, gdzie Pp to pole podstawy, a Pb to pole powierzchni bocznej.
Objętość (V): V = Pp * H, gdzie Pp to pole podstawy, a H to wysokość graniastosłupa.

Pamiętaj! Żeby obliczyć pole podstawy (Pp), musisz znać wzory na pole odpowiedniego wielokąta (trójkąta, kwadratu, prostokąta, itd.).

Zadania z Graniastosłupów – Gdzie Szukać Materiałów?

Pewnie zastanawiasz się teraz, gdzie znaleźć zadania z graniastosłupów w formacie PDF. Oto kilka propozycji:

Strony internetowe z materiałami edukacyjnymi: Wiele stron oferuje darmowe materiały do pobrania, w tym arkusze z zadaniami z matematyki. Wpisz w wyszukiwarkę frazy takie jak "graniastosłupy zadania 8 klasa PDF" lub "matematyka 8 klasa graniastosłupy zadania".
Zbiory zadań do matematyki dla ósmej klasy: To sprawdzone źródło zadań, często z rozwiązaniami.
Podręcznik do matematyki: Twój podręcznik powinien zawierać zadania z graniastosłupów. Wykorzystaj go!
Serwisy oferujące korepetycje online: Często udostępniają one darmowe materiały, aby zachęcić do korzystania z ich usług.
Portale edukacyjne: Szukaj na platformach edukacyjnych, które oferują testy i ćwiczenia interaktywne z matematyki.

Pamiętaj! Nie ograniczaj się tylko do jednego źródła. Im więcej materiałów przejrzysz, tym lepiej zrozumiesz temat.

Jak Efektywnie Uczyć Się Rozwiązywania Zadań?

Samo posiadanie zadań to nie wszystko. Ważne jest, żeby umieć się uczyć efektywnie. Oto kilka wskazówek:

Zacznij od podstaw: Upewnij się, że rozumiesz definicję graniastosłupa i znasz podstawowe wzory.
Rozwiąż kilka prostych przykładów: Na początek wybierz zadania, w których masz podane wszystkie potrzebne dane. Stopniowo przechodź do zadań bardziej skomplikowanych.
Krok po kroku: Rozwiązuj zadania krok po kroku, zapisując wszystkie obliczenia. To pomoże ci uniknąć błędów i lepiej zrozumieć proces rozwiązywania.
Sprawdzaj rozwiązania: Po rozwiązaniu zadania sprawdź, czy twoja odpowiedź jest poprawna. Jeśli nie, spróbuj znaleźć błąd w swoich obliczeniach.
Szukaj pomocy: Jeśli masz problem z zadaniem, nie wstydź się prosić o pomoc. Zapytaj nauczyciela, kolegę lub korepetytora.
Powtarzaj: Regularnie powtarzaj rozwiązywanie zadań. To pomoże ci utrwalić wiedzę i przygotować się do sprawdzianu.
Wykorzystuj wizualizacje: Rysuj graniastosłupy, żeby lepiej zrozumieć ich budowę i właściwości. Możesz też korzystać z programów komputerowych do modelowania 3D.

Kluczowa jest systematyczność! Lepiej uczyć się regularnie po trochę, niż wszystko na ostatnią chwilę.

Częste Błędy i Jak Ich Unikać

Podczas rozwiązywania zadań z graniastosłupów uczniowie często popełniają pewne błędy. Poznaj je, żeby ich unikać:

Pomylenie wzorów: Upewnij się, że dobrze znasz wzory na pole powierzchni całkowitej i objętość graniastosłupa, a także wzory na pole podstawy (w zależności od jej kształtu).
Błędy w obliczeniach: Starannie sprawdzaj swoje obliczenia, szczególnie przy mnożeniu i dzieleniu.
Złe jednostki: Pamiętaj o używaniu odpowiednich jednostek (np. cm, m, cm², m³, itd.).
Niezrozumienie treści zadania: Przeczytaj uważnie treść zadania i upewnij się, że wiesz, co masz obliczyć.
Brak rysunku pomocniczego: Narysuj graniastosłup, żeby lepiej zrozumieć zadanie i zlokalizować potrzebne dane.

Przeciwności? Zmień je w Możliwości!

Niektórzy mogą uważać, że nauka o graniastosłupach jest nudna i niepotrzebna. Mogą argumentować, że w życiu codziennym nie będą musieli obliczać ich pól i objętości. Jednak, jak już wspomniałem, geometria rozwija umiejętności logicznego myślenia i rozwiązywania problemów, które przydadzą się w wielu dziedzinach życia.

Poza tym, zrozumienie geometrii pozwala lepiej rozumieć świat wokół nas. Zwróć uwagę na kształty budynków, mebli, przedmiotów codziennego użytku. Zobaczysz, że geometria jest wszędzie! To nie tylko suche wzory i obliczenia, ale fascynujący sposób na poznawanie świata.

Podsumowanie i Co Dalej?

Graniastosłupy w ósmej klasie to ważny temat, ale z pewnością do opanowania! Pamiętaj o podstawowych definicjach, wzorach i systematycznej pracy. Nie zrażaj się trudnościami, szukaj pomocy, i wykorzystuj dostępne materiały (w tym PDF-y z zadaniami).

Zatem, jakie konkretne działanie podejmiesz dzisiaj, żeby zbliżyć się do mistrzostwa w graniastosłupach? Czy to będzie rozwiązanie jednego zadania, powtórzenie wzorów, czy poszukanie ciekawych materiałów edukacyjnych online? Wybierz coś i zacznij działać! Powodzenia!