Graniastoslupy 8 Klasa Zadania

Rozumiem, że zadania z graniastosłupów w 8 klasie mogą sprawiać sporo kłopotów. Geometria przestrzenna potrafi być wyzwaniem, szczególnie gdy zaczyna się od wizualizacji i obliczeń różnych figur. Pamiętaj, nie jesteś sam! Wielu uczniów mierzy się z podobnymi trudnościami. Ale spokojnie, przejdziemy przez to razem.

Zastanówmy się, dlaczego graniastosłupy są ważne? To nie tylko suche wzory i nudne obliczenia. Graniastosłupy otaczają nas wszędzie! Pomyśl o budynkach, pudełkach, a nawet o niektórych elementach mebli. Zrozumienie ich właściwości pozwala na projektowanie, budowanie i optymalizację wielu rzeczy w naszym otoczeniu. To podstawa architektury, inżynierii i wielu innych dziedzin!

Często słyszę opinie, że geometria przestrzenna jest bezużyteczna w życiu codziennym. "Po co mi to?" - pytacie. To prawda, że nie będziesz codziennie obliczać objętości graniastosłupa. Ale ćwiczy to twoje logiczne myślenie, wyobraźnię przestrzenną i umiejętność rozwiązywania problemów. Te umiejętności są nieocenione w każdej dziedzinie życia!

Zatem, jak efektywnie rozwiązywać zadania z graniastosłupów? Podzielmy to na kilka kluczowych elementów:

Podstawowe definicje i wzory

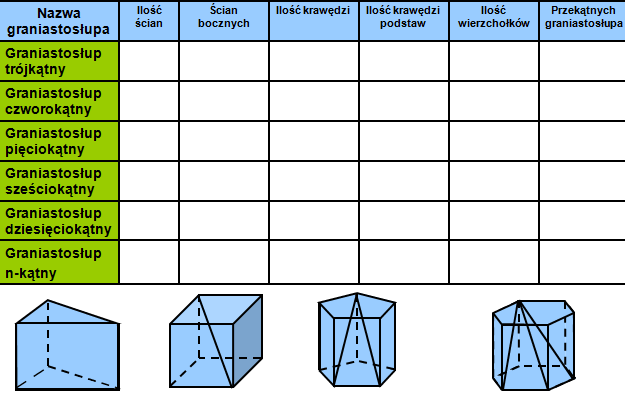
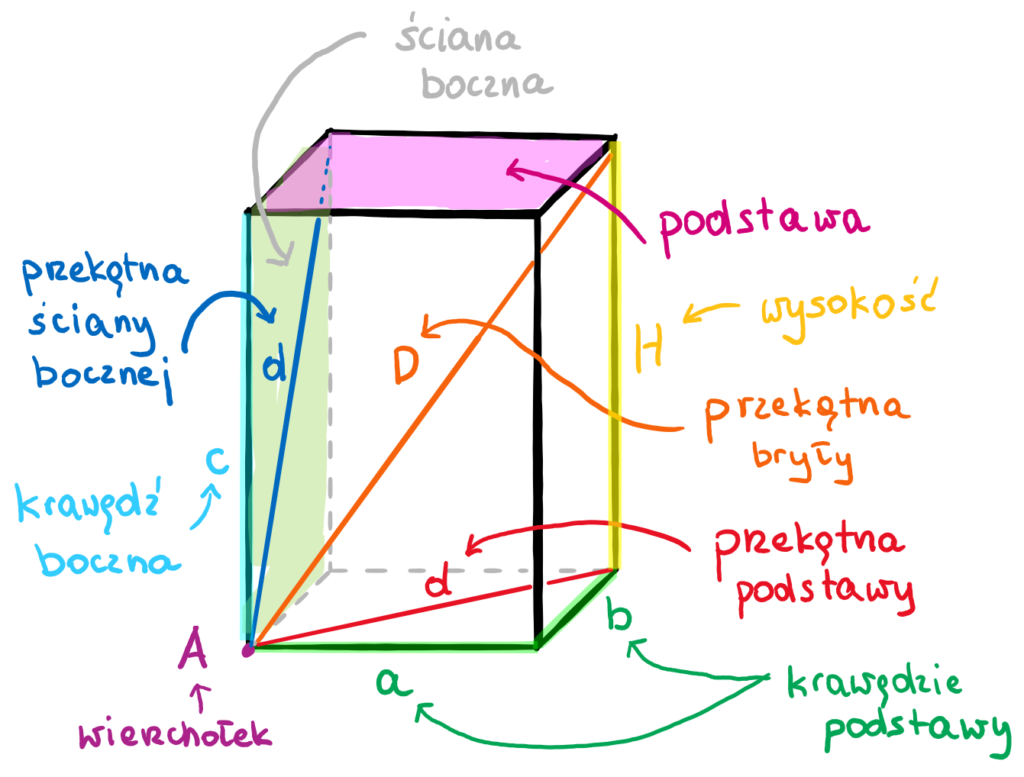
Zacznijmy od podstaw. Czym jest graniastosłup? To bryła geometryczna, która ma dwie identyczne i równoległe podstawy, połączone ścianami bocznymi, które są równoległobokami (najczęściej prostokątami). Ważne jest rozróżnienie kilku typów graniastosłupów:

Graniastosłup prosty: Ściany boczne są prostopadłe do podstawy.
Graniastosłup prawidłowy: Graniastosłup prosty, którego podstawą jest wielokąt foremny (np. trójkąt równoboczny, kwadrat, pięciokąt foremny).
Graniastosłup pochyły: Ściany boczne nie są prostopadłe do podstawy.

Kluczowe wzory, które musisz znać:

Pole powierzchni całkowitej (Pc): Pc = 2Pp + Pb, gdzie Pp to pole podstawy, a Pb to pole powierzchni bocznej.
Objętość (V): V = Pp * H, gdzie Pp to pole podstawy, a H to wysokość graniastosłupa.

Pole podstawy (Pp)

Obliczanie pola podstawy zależy od tego, jaki wielokąt jest podstawą graniastosłupa. Przypomnij sobie wzory na pola:

Trójkąta: Pp = (a * h) / 2, gdzie a to podstawa trójkąta, a h to wysokość trójkąta.
Kwadratu: Pp = a², gdzie a to długość boku kwadratu.
Prostokąta: Pp = a * b, gdzie a i b to długości boków prostokąta.
Równoległoboku: Pp = a * h, gdzie a to podstawa równoległoboku, a h to wysokość równoległoboku.
Trapezu: Pp = ((a + b) * h) / 2, gdzie a i b to długości podstaw trapezu, a h to wysokość trapezu.
Wielokąta foremnego: W przypadku wielokątów foremnych o większej liczbie boków, często korzysta się ze wzorów lub dzieli wielokąt na mniejsze figury (np. trójkąty).

Pole powierzchni bocznej (Pb)

Pole powierzchni bocznej to suma pól wszystkich ścian bocznych. W przypadku graniastosłupa prostego, ściany boczne są prostokątami, więc obliczenie Pb jest stosunkowo proste. Wystarczy zsumować pola wszystkich prostokątów.

Pb = Obwód podstawy * Wysokość graniastosłupa

Strategie rozwiązywania zadań

Teraz przejdźmy do konkretnych strategii, które pomogą Ci w rozwiązywaniu zadań:

Zrozum treść zadania: Przeczytaj uważnie zadanie kilka razy. Zidentyfikuj, co jest dane, a co trzeba obliczyć. Zrób szkic bryły, zaznacz na nim dane.
Wybierz odpowiedni wzór: Zastanów się, które wzory są potrzebne do rozwiązania zadania. Upewnij się, że rozumiesz, co oznaczają poszczególne symbole we wzorach.
Wykonaj obliczenia krok po kroku: Nie spiesz się. Wykonuj obliczenia krok po kroku, zapisując wszystkie etapy. Unikniesz w ten sposób błędów.
Sprawdź jednostki: Upewnij się, że wszystkie wielkości są wyrażone w tych samych jednostkach. Jeśli nie, przelicz je.
Sprawdź wynik: Czy wynik ma sens? Czy jest realistyczny? Zastanów się, czy wynik mógłby być większy lub mniejszy.

Przykładowe zadania i rozwiązania

Zadanie 1: Podstawą graniastosłupa prostego jest trójkąt równoboczny o boku 6 cm. Wysokość graniastosłupa wynosi 10 cm. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.

Rozwiązanie:

Pole podstawy (Pp): Wzór na pole trójkąta równobocznego to Pp = (a²√3) / 4. Zatem Pp = (6²√3) / 4 = 9√3 cm².
Obwód podstawy: Obwód trójkąta równobocznego to 3a = 3 * 6 = 18 cm.
Pole powierzchni bocznej (Pb): Pb = Obwód podstawy * Wysokość = 18 * 10 = 180 cm².
Pole powierzchni całkowitej (Pc): Pc = 2Pp + Pb = 2 * 9√3 + 180 = 18√3 + 180 cm².
Objętość (V): V = Pp * H = 9√3 * 10 = 90√3 cm³.

Zadanie 2: Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku 4 cm. Przekątna ściany bocznej ma długość 5 cm. Oblicz objętość tego graniastosłupa.

Rozwiązanie:

Wysokość graniastosłupa (H): Przekątna ściany bocznej tworzy trójkąt prostokątny z bokiem kwadratu i wysokością graniastosłupa. Z twierdzenia Pitagorasa: H² + 4² = 5². Zatem H² = 25 - 16 = 9, więc H = 3 cm.
Pole podstawy (Pp): Pp = a² = 4² = 16 cm².
Objętość (V): V = Pp * H = 16 * 3 = 48 cm³.

Częste błędy i jak ich unikać

Pomylenie wzorów: Upewnij się, że używasz odpowiednich wzorów dla danej figury.
Błędy w obliczeniach: Sprawdzaj obliczenia krok po kroku.
Zapominanie o jednostkach: Pamiętaj o jednostkach i upewnij się, że są spójne.
Brak wizualizacji: Spróbuj narysować bryłę, aby lepiej zrozumieć treść zadania.
Pomijanie kroków: Nie spiesz się. Wykonuj obliczenia krok po kroku, zapisując wszystkie etapy.

Dodatkowe wskazówki

Ćwicz regularnie: Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zagadnienie.
Korzystaj z zasobów online: W Internecie znajdziesz wiele materiałów edukacyjnych, w tym filmów instruktażowych i interaktywnych ćwiczeń.
Poproś o pomoc: Jeśli masz trudności, nie bój się poprosić o pomoc nauczyciela, kolegów lub korepetytora.
Zrozumienie, a nie zapamiętywanie: Staraj się zrozumieć, dlaczego dany wzór działa, zamiast go tylko zapamiętywać.

Pamiętaj, że nauka geometrii przestrzennej wymaga czasu i cierpliwości. Nie zrażaj się początkowymi trudnościami. Z każdym rozwiązanym zadaniem będziesz czuł się pewniej i zdobędziesz nowe umiejętności. A w końcu, kto wie, może sam zostaniesz architektem i zaprojektujesz niesamowity budynek?

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć zadania z graniastosłupów. Czy masz jakieś pytania lub wątpliwości, które chciałbyś omówić?