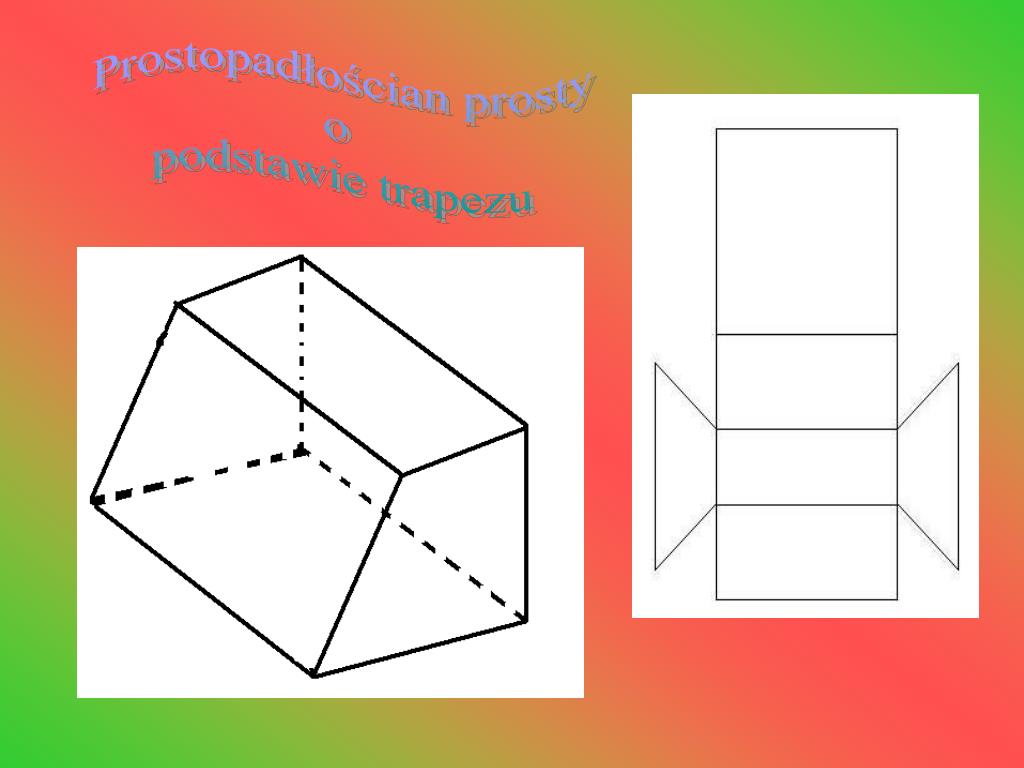
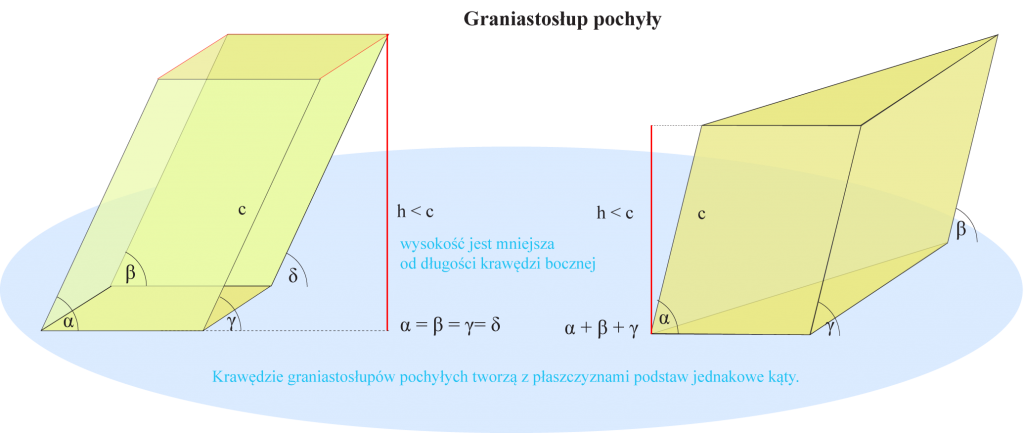
Graniastosłup Prosty O Podstawie Trapezu

Zacznijmy od podstaw. Czym właściwie jest graniastosłup? Najprościej mówiąc, to bryła geometryczna, która ma dwie identyczne podstawy, połączone ścianami bocznymi będącymi równoległobokami. Jeżeli te ściany boczne są prostokątami i tworzą kąt prosty z podstawami, mamy do czynienia z graniastosłupem prostym. A co, jeśli podstawą takiego graniastosłupa jest trapez? Wtedy mówimy właśnie o graniastosłupie prostym o podstawie trapezu.
Definicja i Podstawowe Pojęcia
Graniastosłup prosty o podstawie trapezu to trójwymiarowa figura geometryczna charakteryzująca się następującymi cechami:
- Podstawy: Dwie identyczne podstawy w kształcie trapezu. Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych. Boki równoległe nazywamy podstawami trapezu (często oznaczane jako a i b), a pozostałe dwa boki to ramiona trapezu (często oznaczane jako c i d).
- Ściany boczne: Prostokąty, prostopadłe do podstaw. Ich liczba odpowiada liczbie boków trapezu, czyli w tym przypadku mamy cztery prostokątne ściany boczne.
- Wysokość graniastosłupa (H): Odległość między podstawami. Jest ona równa długości krawędzi bocznej, ponieważ ściany boczne są prostokątami.
Warto przypomnieć, że istnieją różne rodzaje trapezów:
- Trapez równoramienny: Trapez, którego ramiona są równej długości.
- Trapez prostokątny: Trapez, który ma co najmniej jeden kąt prosty.
- Trapez różnoboczny: Trapez, którego wszystkie boki mają różne długości.
Rodzaj trapezu, który stanowi podstawę graniastosłupa, wpływa na właściwości i obliczenia związane z danym graniastosłupem.
Obliczanie Pola Powierzchni i Objętości
Kluczowe dla zrozumienia graniastosłupa prostego o podstawie trapezu są umiejętności obliczania jego pola powierzchni i objętości.
Pole Powierzchni
Pole powierzchni całkowitej (Pc) graniastosłupa to suma pól wszystkich jego ścian. Składa się ono z dwóch pól podstaw (Pp) i pola powierzchni bocznej (Pb). Zatem:
Pc = 2Pp + Pb
Gdzie:
- Pp to pole trapezu. Wzór na pole trapezu to: Pp = ½ (a + b) * h, gdzie a i b to długości podstaw trapezu, a h to wysokość trapezu (odległość między podstawami).
- Pb to suma pól wszystkich czterech prostokątnych ścian bocznych. Jeżeli długości boków trapezu (podstawy graniastosłupa) oznaczymy jako a, b, c i d, a wysokość graniastosłupa jako H, to: Pb = aH + bH + cH + dH = H(a + b + c + d). Zauważ, że (a + b + c + d) to obwód trapezu.
Podsumowując, wzór na pole powierzchni całkowitej graniastosłupa prostego o podstawie trapezu to:
Pc = 2 * [½ (a + b) * h] + H(a + b + c + d) = (a + b) * h + H(a + b + c + d)
Objętość
Objętość (V) graniastosłupa to iloczyn pola podstawy i wysokości. W przypadku graniastosłupa prostego o podstawie trapezu:
V = Pp * H
Gdzie:
- Pp to pole trapezu (jak wyżej: Pp = ½ (a + b) * h).
- H to wysokość graniastosłupa.
Zatem wzór na objętość graniastosłupa prostego o podstawie trapezu to:
V = ½ (a + b) * h * H
Przykłady i Zastosowania
Wyobraźmy sobie, że mamy graniastosłup prosty o podstawie trapezu równoramiennego. Podstawy trapezu mają długości a = 5 cm i b = 3 cm, wysokość trapezu h = 2 cm, a wysokość graniastosłupa H = 8 cm. Ramiona trapezu mają długość c = 2.24 cm (można wyliczyć z twierdzenia Pitagorasa, dzieląc trapez równoramienny na prostokąt i dwa trójkąty prostokątne). Obliczmy pole powierzchni całkowitej i objętość.
Pole powierzchni:
Pc = (5 + 3) * 2 + 8 * (5 + 3 + 2.24 + 2.24) = 16 + 8 * 12.48 = 16 + 99.84 = 115.84 cm²
Objętość:
V = ½ * (5 + 3) * 2 * 8 = 8 * 8 = 64 cm³
Zastosowania graniastosłupa prostego o podstawie trapezu można znaleźć w architekturze (np. w elementach konstrukcyjnych dachów), w budownictwie (np. w fundamentach), a także w przemyśle (np. w projektowaniu niektórych rodzajów opakowań lub kształtowników). Wyobraźmy sobie betonowy element podtrzymujący schody – często ma on właśnie kształt graniastosłupa prostego o podstawie trapezu, aby zapewnić odpowiednią stabilność i rozkład sił.
Podsumowanie
Graniastosłup prosty o podstawie trapezu to interesująca figura geometryczna, której znajomość przydaje się w wielu dziedzinach. Kluczem do opanowania tego zagadnienia jest zrozumienie definicji, właściwości i wzorów na pole powierzchni i objętość. Pamiętaj, aby dokładnie analizować kształt trapezu będącego podstawą, ponieważ ma to wpływ na obliczenia i charakterystykę całej bryły.